Задания
Первый тур (10 минут; каждая задача - 6 баллов).
1.1. Найдите наименьшее и наибольшее значение выражения аsin2x + bcos2x, где a и b - действительные числа.
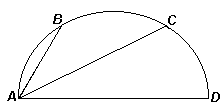
1.2. Точки В и С делят полуокружность с диаметром
AD на три равные части (см. рис.). Найдите площадь фигуры САВ,
ограниченной хордами АВ и АС и дугой ВС, если радиус
полуокружности равен R.
1.3. Пусть S(x) - сумма цифр натурального числа x. Решите уравнение: x + S(x) = 2001.
Второй тур (15 минут; каждая задача - 7 баллов).
2.1. Приведенный квадратный трехчлен P(x) имеет положительный дискриминант D. Сколько корней имеет уравнение P(x) + P(x+D1/2) = 0?
2.2. В треугольнике ABC биссектриса AE равна отрезку EC. Найдите углы треугольника АВС, если известно, что AC = 2AB.
2.3. Существуют ли 6 последовательных натуральных чисел таких, что наименьшее общее кратное первых трех из них больше, чем наименьшее общее кратное трех следующих?
Третий тур (15 минут; каждая задача - 7 баллов).
3.1. Найдите все значения а, для которых уравнение ax2 - 2x + 2a2 - 4 = 0 имеет только целые корни.
3.2. О - центр окружности, описанной около треугольника АВС. Точка D лежит на стороне АС, причем отрезок BD перпендикулярен прямой AO. Найдите длину отрезка AD, если АС = b; АВ = с.
3.3. Дана кучка из 2001 камня. Ее требуется разбить на 2001 кучку по одному камню в каждой, причем за один "шаг" разрешается разбивать любую из уже имеющихся кучек камней на две непустые кучки. На каждом "шаге": если количество камней в двух кучках, получающихся при разбиении, различно, то оплачивается штраф - 1 рубль, если же оно одинаково, то штраф не платится. Какой наименьший штраф придется заплатить для того, чтобы осуществить указанное разбиение?
Четвертый тур (20 минут; каждая задача - 8 баллов).
4.1. Функция f(x) при всех действительных x удовлетворяет уравнению 2f(x) + f(x2-1) = 1. Какие значения может принимать f(-21/2) ?
4.2. Существуют ли четыре точки А, В, С и D, не лежащие в одной плоскости, такие, что каждый из треугольников АВС, ABD, ACD и BCD является тупоугольным?
4.3. На плоскости задано конечное множество точек так, что для любых двух точек А и В из данного множества существует точка М из этого же множества такая, что /АМВ = a, где a - фиксированное число. Найдите значение a.
Пятый тур (25 минут; каждая задача - 9 баллов).
5.1. Сколько действительных корней имеет уравнение: x37 + x8 + 1 = 0?
5.2. Существуют ли на плоскости два выпуклых четырехугольника такие, что стороны каждого из них лежат на серединных перпендикулярах к сторонам другого?
5.3. Кучку из N спичек произвольным образом разбили на две кучки, подсчитали количество спичек в каждой кучке и записали их произведение. Затем, одну из новых кучек опять разбили на две, опять подсчитали количество спичек в каждой и записали новое произведение. Этот процесс продолжали до тех пор, пока не получили N кучек по одной спичке в каждой. Тогда, все полученные произведения сложили и получили число S. Найдите S.