Зимний турнир Архимеда 20.01.2002

Личная олимпиада для 6-7 классов.

Условия и решения задач

1. (3 балла) Расставьте скобки в неверном равенстве 2:3:4:5:6=5 так, чтобы оно стало верным.
Ответ: (2:3):(4:5:6)=5.
Ответ единственный, но доказывать этого не требуется.

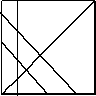
2. (4 балла) Прямые и квадрат. На листе бумаги нарисован квадрат. Можно ли разрезать его по 4 прямым линиям на 2 треугольника и 8 четырехугольников? Если можно, приведите пример, если нет, объясните почему.
Ответ: например, см. рис. 1 или рис. 2.

рис. 1		рис. 2

Ответ "можно" без примера - 0 баллов.

3. (6 баллов) Грузовик. Известно, что грузовик можно заполнить ровно 109 способами упаковками в 3 кг и 5 кг помидоров так, чтобы их общий вес составил x кг. Чему равно x?

Ответ. 1620; 1623; 1625; 1626; 1628 - 1634; 1636; 1637; 1639; 1642 (15 чисел).

Решение. Условию задачи удовлетворяют наборы вида x=5*3m+3*5n, причем m может принимать значения 0, 1, 2 , ... , 108, а n соответственно 108, 107, ... 1, 0. То есть x=15*108=1620 кг является одним из решений задачи. Заметим, что 3 упаковки по 5 кг и 5 упаковок по 3 кг весят одинаково. Выделим наборы из 3 упаковок по 5 кг и 5 упаковок по 3 кг. Тогда x=5*3m+3*5n+5a+3b, где а принимает значения 0, 1, 2; b принимает значения 0, 1, 2, 3, 4. Можно доказать, что тогда числа а и b восстанавливаются однозначно (алгоритм Евклида или полный перебор). Следовательно, выражение c = m + n представляется в виде суммы двух слагаемых ровно ста девятью способами, то есть с = 108. Таким образом, условию задачи удовлетворяют все наборы вида x=1620+5a+3b, где a может принимать значения 0, 1, 2, а b - 0, 1, 2, 3, 4 - причем независимо друг от друга.

Приведен один из возможных ответов без обоснований - 1 балл;
один из возможных ответов получен в результате верных рассуждений - 3 балла; <ИК>задача решена полностью исходя из предположения, что должны быть упаковки обоих видов (15*109=1635 кг) - 5 баллов.

4. (5 баллов) В саду Деда Мороза вот уже более 1000 лет растет Волшебная елка. Известно, что каждое утро на ней вырастают 100 иголок, и каждая иголка живет ровно 4 года, а затем отмирает. Сколько же всего иголок на Волшебной елке?

Ответ. 146100 иголок.

Решение. Заметим, что после первых четырех лет жизни елки количество иголок перестанет меняться, так как каждый день 100 иголок будут вырастать, и 100 - отмирать. Значит, после того, как Волшебной елке исполнилось 4 года, количество иголок на ней равно 1461х100 = 146100 и больше не менялось (т.к. в четырех годах 1461 дней).

Присуствует идея "стабилизации" количества иголок через 4 года - 2 балла;
сформулирован характер изменения количества иголок с учетом високосных лет - еще 2 балла;
верный подсчет - 1 балл.

5. (10 баллов) Мартышка и бананы. Мартышка собрала 100 бананов общим весом 10 кг. Помогите Мартышке накормить этими бананами Слоненка и Удава так, чтобы никто из них не обиделся: они могут обидеться, если один съест бананов хотя бы на 100 г больше другого. (Вес одного банана от 20 до 200 г, мартышка может узнать вес каждого банана.)

Решение. Бананы, вес которых больше 100 г, будем называть большими, а все остальные бананы - маленькими. Положим все бананы в левую кучку (ее сумма Л) и начнем перекладывать по одному банану в правую в порядке убывания веса (сумма правой кучки П). Допустим, что на каком-то шаге Л>П+100, а на следующем Л-х+100<П+х (иначе в один из двух моментов мы получим искомое разложение на 2 кучки); Л<П+400 (иначе при перекладывании х неравенство бы сохранилось). Вернем х на место и попробуем перекладывать другие бананы из Л в П. Пусть при попытке преложить любой большой банан, будет Л-б+100<П+б, а при попытке переложить маленький Л-м>П+м-100. Переложим все маленькие направо по очереди. Либо в процессе разница станет <100 (мы перекладывам маленькие бананы), либо переложив все(М) маленькие бананы все имеем Л-М>П+М+100. Учитывая Л<П+400 получим М<150, но м>20, число маленьких бананов <7. Так как число тяжелых >93 и сумма их <9850, то среднее арифметическое тяжелых бананов <106 пусть у - самый легкий из тяжелых у<106 и у лежит в Л; мы знаем, что Л-у+100<П+у (перложив любой тяжелый, например у, перевесит П хотя бы на 100) и что Л-м>П+м+100 (при перекладывании м направо Л будет тяжлее хотя бы на 100), значитуу-м>100 но у<106, м>20 значит одно из последних неравенств неверно, и можно уравновесить одним из этих способов.

6. (8 баллов) На доске написано число 19921993...20012002. Разобьем произвольным образом его десятичную запись на два числа и сложим их. С полученным числом проделаем аналогичную операцию и т. д., до тех пор пока не получится однозначное число. Какое число может получиться? Исследуйте все возможности.

Ответ: 7.

Решение. Пусть в результате разбиения получены числа x и y, тогда исходное число имело вид x*10...0 и y, а число, полученное в результате разбиения -(x+y). Рассмотрим разность этих чисел: (x*10...0+y)-(x+y)=99...9x. Так как эта разность кратна 9, то исходное и полученное число имеют одинаковые остатки от деления на 9. Следовательно, каждый раз, при выполнении указанной операции этот остаток является инвариантом.
Остаток при делении на 9 числа 19921993...20012002 равен 7.

Верный ответ без обоснований - 1 балл;
есть идея инварианта, но решение не доведено до конца - 5 баллов;
разумная попытка обоснования идеи - 6 баллов.

Список победителей