Личная олимпиада | варианты: 1, 2, 3, 3(0), 4А, 4Б, 5 | zip-архив (19812 байт)
1. Нарисуйте шестиугольник, который жюри не сможет разрезать на два четырехугольника. (С. Г. Волченков)
2. В каждой клетке доски размером 16*30 сидит по жуку. Могут ли жуки перелететь на доску размером 15*32, в каждую клетку по одному жуку, чтобы жуки, бывшие соседями на доске 16*30, оказались соседями и на новой доске? (Соседи - жуки, сидящие в клетках с общей стороной.) (И. Жук, г. Гродно)
3. В следующих многозначных числах цифры заменены буквами (одинаковые цифры - одинаковыми буквами, а разные - разными). Оказалось, что ДЕВЯНОСТО делится на 90, а ДЕВЯТКА делится на 9. Может ли СОТКА делиться на 9?
4. Можно ли первые 2001 натуральных чисел расставить по кругу так, чтобы каждое число делилось на разность своих соседей?
5. Натуральное число разрешено увеличить на любое целое число процентов от 1 до 100 процентов, если при этом получаем натуральное число. Найдите наименьшее натуральное число, которое нельзя при помощи таких операций получить из числа 1. (А. Шаповалов)
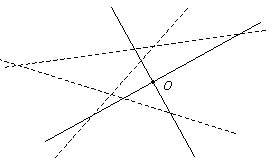
6. Оси Ox и Oy и прямые y=ax+b, y=bx+c, y=cx+a расположены так, как показано на рисунке 1. Укажите ось Ox и положительное направление на ней. (С. Токарев)
 |
| Рис. 1 |
7. Двое играют в шахматы, а еще шестеро желающих сыграть образуют очередь. Проигравший партию становится в конец очереди; тот, чья очередь подошла, играет с победителем и так далее. Может ли в какой-то момент оказаться так, что каждые двое сыграли между собой ровно один раз? (С. Токарев)
1. Изобразите на координатной плоскости множество точек (x, y), для которых ((x+y)/2)3=(x3+y3)/2
2. В клетках квадратной таблицы 3*3 расставлены числа 1, 2, 3, ..., 9 так, что сумма каждых четырех чисел, заполняющих квадрат 2*2, равна одному и тому же числу S. Найдите все возможные значения S.
3. Докажите, что существуют различные стозначные числа A и B, являющиеся точными кубами, что цифры десятичной записи числа A, записанные в обратном порядке, образуют число B.
4. В выпуклом четырехугольнике проведены биссектрисы всех его углов. Может ли каждая из сторон четырехугольника пересекаться какой-либо биссектрисой в точке, отличной от вершины?
5. Рассматриваются все трехчлены вида ax2+bx+c с натуральными коэффициентами, не превосходящими 100. Каких трехчленов больше: имеющих действительные корни или не имеющих?
6. Сторона BC треугольника ABC разбита точками M и N на три равные части (BM=MN=NC); K и L - середины сторон AB и AC соответственно. Прямая LM пересекает прямую AB в точке E, прямая KN пересекает прямую AC в точке F. Докажите, что прямая EF параллельна прямой BC.
7. Найдите все натуральные n, которые равны сумме некоторых трех различных натуральных делителей числа n-1.
8. У нас есть куча монет. Известно, что настоящих среди них больше, чем фальшивых, все настоящие монеты весят одинаково. Любая фальшивая монета отличается по весу от настоящей, но фальшивые монеты могут иметь разный вес. Мы можем пользоваться чашечными весами, владелец которых после каждого взвешивания забирает себе (в качестве нашей платы) любую выбранную им монету из взвешенных. Докажите, что можно выделить хотя бы одну настоящую монету, которая останется у нас.
1. Среди первых 60 натуральных чисел произвольно выбрано 30+n (где 1<n<30) различных чисел. Докажите, что среди выбранных чисел всегда найдутся 2n чисел таких, что их сумма равна 61n. (C. С. Тасмуратов)
2. Решите в натуральных числах x, y, z и t уравнение x2+y2+z2=2t. (В. В. Произволов)
3. Играя в домино, Мустафа, Табриз, Гамид и Эльмир взяли по семь костей с различной суммой очков. При этом сумма очков Мустафы и Табриза оказалась равной сумме очков Гамида и Эльмира, а разница очков Мустафы и Табриза составила 27/7 разницы очков Гамида и Эльмира. Укажите какие-нибудь 12 костей домино, которые находятся на руках у Мустафы и Табриза. (Р. Мустафаев)
4. Из бумаги склеили правильный тетраэдр. Разрежьте его на 12 одинаковых бумажных равносторонних треугольников. (В. В. Произволов)
5. Могут ли длины сторон x, y и z какого-нибудь
треугольника удовлетворять неравенству:
x3+y3+z3+2xyz
>
x2(y+z)+y2(z+x)+z2(x+y)?
(Д. А. Калинин)
6. У крестообразно пересекающихся четырехугольников соответствующие стороны параллельны и отстоят друг от друга на расстояние 1 (рисунок 1). Докажите, что периметры четырехугольников равны. (В. В. Произволов)
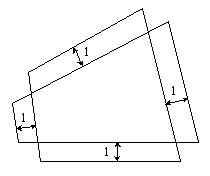 |
| Рис. 1 |
7. В некоторых клетках шахматной доски проведена одна из двух возможных диагоналей так, что ни для каких двух диагоналей концы их не совпадают. Какое наибольшее количество диагоналей можно провести, соблюдая такое условие? (И. Ф. Акулич)
8. Дан выпуклый шестиугольник ABCDEF, в котором AB=CD=EF, /A=/C=/E и /B=/D=/F. Докажите, что BC=DE=FA. (В. В. Произволов)
1. В Чебабурге имеют хождение монеты трех видов: 1, 2 и 5 талеров. Масса каждой монеты одного из видов (в унциях) совпадает с ее достоинством (в талерах), масса каждой монеты другого вида в полтора раза больше ее достоинства, а масса каждой монеты третьего вида - в два раза больше. Имеется неограниченный запас монет каждого вида и чашечные весы без гирь. Какое наименьшее количество взвешиваний позволит наверняка определить массу монет каждого достоинства? (И. Акулич)
2. В равнобедренном треугольнике ABC (AB=BC) проведена биссектриса AM. Найдите углы треугольника, если известно, что BM=AC. (Д. Калинин)
3. Решите систему уравнений:
x(1+y1/2)=y(1+z1/2)=z(1+x1/2)=2
4. Пусть M - конечное подмножество множества целых чисел, причем количество элементов в M кратно четырем, а между любыми двумя числами, не принадлежащими M, расположено четное количество элементов из M. Докажите, что M можно разбить на две части с равным числом элементов и равной суммой. (С. Волченков)
5. Клетчатый прямоугольник 2*3 сложен из 17 спичек, как показано на рисунке 1. Какие размеры может иметь клетчатый прямоугольник, составленный из 1000 таких же спичек? (А. Шаповалов)
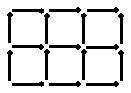 |
| Рис. 1 |
6. На стороне АВ равностороннего треугольника АВС, отмечена точка C1, а на стороне АС - точка В1 так, что ВC1=AВ1=АВ:3; М - точка пересечения отрезков ВВ1 и СC1. Найдите угол АМС. (Д. Калинин)
7. Можно ли в кубе с ребром 2000 разместить 7 точек так, чтобы расстояние между любыми двумя было бы больше 2001? Точки можно помещать и на поверхности куба. (С. Волченков)
8. Целые числа x, y, z таковы, что числа xy+1, yz+1 и zx+1 являются полными квадратами. Докажите, что произведение xyz делится на 8. (В. Сендеров)
1. В Чебабурге имеют хождение монеты трех видов: 1, 2 и 5 талеров. Масса каждой монеты одного из видов (в унциях) совпадает с ее достоинством (в талерах), масса каждой монеты другого вида в полтора раза больше ее достоинства, а масса каждой монеты третьего вида - в два раза больше. Имеется неограниченный запас монет каждого вида и чашечные весы без гирь. Какое наименьшее количество взвешиваний позволит наверняка определить массу монет каждого достоинства? (И. Акулич)
2. В равнобедренном треугольнике ABC (AB=BC) проведена биссектриса AM. Найдите углы треугольника, если известно, что BM=AC. (Д. Калинин)
3. Решите систему уравнений:
x(1+y1/2)=y(1+z1/2)=z(1+x1/2)=2
4. Пусть M - конечное подмножество множества целых чисел, причем количество элементов в M кратно четырем, а между любыми двумя числами, не принадлежащими M, расположено четное количество элементов из M. Докажите, что M можно разбить на две части с равным числом элементов и равной суммой. (С. Волченков)
5. Клетчатый прямоугольник 2*3 сложен из 17 спичек, как показано на рисунке. Какие размеры может иметь клетчатый прямоугольник, составленный из 1000 таких же спичек? (А. Шаповалов)
 |
| Рис. 1 |
6. На стороне АВ равностороннего треугольника АВС, отмечена точка C1, а на стороне АС - точка В1 так, что ВC1=AВ1=АВ:3; М - точка пересечения отрезков ВВ1 и СC1. Найдите угол АМС. (Д. Калинин)
7. Можно ли в кубе с ребром 2000 разместить 7 точек так, чтобы расстояние между любыми двумя было бы больше 2001? Точки можно помещать и на поверхности куба. (С. Волченков)
8. Целые числа x, y, z таковы, что числа xy+1, yz+1 и zx+1 являются полными квадратами. Докажите, что произведение xyz делится на 8. (В. Сендеров)
1. На турнир съехалось 105 школьников. Оказалось, что среди любых пятнадцати есть школьники, знакомые между собой. Кроме того, любые два школьника, имеющие одинаковое количество знакомых среди участников турнира - не знакомы между собой, а имеющие разное количество знакомых - знакомы между собой. Докажите, что среди участников найдется школьник, знакомый со всеми остальными. (В. Каскевич, г. Минск)
2. Биссектрисы АА1, ВВ1, СС1 остроугольного треугольника АВС пересекаются в точке О. Докажите, что из отрезков ОА1, ОВ1, ОС1 можно составить остроугольный треугольник. (С. Токарев, г. Иваново)
3. На шахматной доске, первоначально пустой, расставляются пешки по следующим правилам: выбираются любые четыре пустые клетки, центры которых являются вершинами квадрата со сторонами, параллельными сторонам доски, после чего на одну из этих клеток ставится пешка. Затем выбираются аналогичные четыре пустые клетки, на них снова ставится пешка, и так далее. Какое наибольшее число пешек можно расставить на доске, соблюдая эти правила? (И. Акулич, г. Минск)
4. Палиндромом называется натуральное число, которое не изменится, если его цифры записать в обратном порядке. Докажите, что для любого простого р;>150 существует палиндром, делящийся на р и содержащий не более 0,23р цифр. (И. Акулич, Минск)
5. В трапеции ABCD основание BC вдвое меньше AD; DD1 - перпендикуляр, опущенный на прямую AB. Докажите, что если окружность, описанная около треугольника BCD1, касается AD, то трапеция - равнобокая. (Д. А. Калинин, Кострома)
6. Степану Фомичу 23 февраля 2001 года выдали премию: 250 рублей 00 копеек. Он решил, используя эти деньги, заработать больше и купить жене подарок. Для этого, начиная со следующего дня, он стал ежедневно посещать казино, где каждый день либо выигрывал 20 рублей, либо проигрывал ровно половину имеющихся у него денег. Подсчитав свои доходы накануне 8 марта, Степан Фомич выяснил, что остался в выигрыше, но барыш оказался невелик - меньше трех рублей. Сколько именно? (И. Акулич, г. Минск)
7. Найдите все пары простых чисел (p, q) при которых уравнение x4+(q-x=p-4 имеет, по крайней мере, один целый корень. (И. Воронович г. Минск)
8. В однокруговом хоккейном турнире все команды набрали разное число очков. (В хоккее за победу дается 2 очка, за ничью 1 очко и за поражение 0 очков.) Оказалось, что команда, занявшая последнее место, выиграла не менее 25% своих матчей, а команда, занявшая второе место, выиграла не более 40% своих матчей. Какое наибольшее количество команд могло участвовать в этом турнире? (И. Воронович, г. Минск)
1. На турнир съехалось 105 школьников. Оказалось, что среди любых пятнадцати есть школьники, знакомые между собой. Кроме того, любые два школьника, имеющие одинаковое количество знакомых среди участников турнира - не знакомы между собой, а имеющие разное количество знакомых - знакомы между собой. Докажите, что среди участников найдется школьник, знакомый со всеми остальными. (В. Каскевич, г. Минск)
2. Биссектрисы АА1, ВВ1, СС1 остроугольного треугольника АВС пересекаются в точке О. Докажите, что из отрезков ОА1, ОВ1, ОС1 можно составить остроугольный треугольник. (С.Токарев, г. Иваново)
3. Какое наибольшее количество королей можно расставить на шахматной доске так, чтобы ровно половина из них не угрожала никому из остальных? (И. Акулич, г. Минск)
4. Палиндромом называется натуральное число, которое не изменится, если его цифры записать в обратном порядке. Докажите, что для любого простого р>150 существует палиндром, делящийся на р и содержащий не более 0,23р цифр. (И. Акулич, Минск)
5. На гипотенузе AB прямоугольного треугольника ABC выбраны точки E и F (точка E расположена между точками A и F) такие, что треугольник CEF - равносторонний; точка D - середина гипотенузы. Докажите, что /DCF=2*/ACE.
6. Степану Фомичу 23 февраля 2001 года выдали премию: 250 рублей 00 копеек. Он решил, используя эти деньги, заработать больше и купить жене подарок. Для этого, начиная со следующего дня, он стал ежедневно посещать казино, где каждый день либо выигрывал 20 рублей, либо проигрывал ровно половину имеющихся у него денег. Подсчитав свои доходы накануне 8 марта, Степан Фомич выяснил, что остался в выигрыше, но барыш оказался невелик - меньше трех рублей. Сколько именно? (И. Акулич, г. Минск)
7. Найдите все пары простых чисел (p, q) при которых уравнение x4+(q-2)x=p-4 имеет, по крайней мере, один целый корень. (И. Воронович г. Минск)
8. В однокруговом хоккейном турнире все команды набрали разное число очков. (В хоккее за победу дается 2 очка, за ничью 1 очко и за поражение 0 очков.) Оказалось, что команда, занявшая последнее место, выиграла не менее 25% своих матчей, а команда, занявшая второе место, выиграла не более 40% своих матчей. Какое наибольшее количество команд могло участвовать в этом турнире? (И. Воронович г. Минск)
1. На территории завода четыре асфальтовые дорожки длиной 10 м каждая образуют квадрат. В двух соседних вершинах квадрата стоят двое рабочих, держа на плечах десятиметровую трубу. Им необходимо, передвигаясь по дорожкам и не выпуская при этом трубы, поменяться местами. Из соображений безопасности разрешается идти со скоростью не больше 1 м/с. За какое наименьшее время рабочие могут справиться с заданием? (Внутри квадрата нет никаких сооружений, создающих помехи при переноске трубы). (И. Акулич, г. Минск)
2. Окружность пересекает стороны равностороннего треугольника в шести точках, как показано на рисунке 1. Докажите, что AB2+CA2+BC2=AC1+BA1+CB1. (В. Произволов)
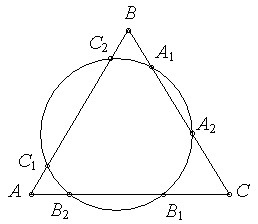 |
| Рис. 1 |
3. Докажите, что ни при каких целых a, b и c
числа
((a-b)/(a-c))-(b/c);
((b-c)/(b-a))-(c/a);
((c-a)/(c-b))-(a/b)
не могут быть целыми одновременно. (В. Каскевич г. Минск)
4. Разрежьте квадрат на шесть частей так, чтобы ими можно было полностью и без перекрытий оклеить поверхность некоторого куба. (С. Токарев)
5. Натуральное число назовем удобным, если его можно представить в виде суммы двух натуральных слагаемых, суммы цифр которых одинаковы. Докажите, что существуют 1000000 последовательных натуральных чисел, являющихся удобными.
6. Рассмотрим множество всех квадратных таблиц p*p клеток (p;>1), заполненных натуральными числами 1, 2, ..., p2. Пусть A - подмножество, в котором каждую таблицу можно получить из правильной операциями перестановки столбцов и перестановки строк (правильная таблица - таблица, в которой в первой строке (столбце) стоят по порядку числа 1, 2, ..., p, во второй строке (столбце) - p+1, p+2, ..., 2p, и так далее); B - подмножество, в котором из любой таблицы можно получить таблицу с равными числами операциями прибавления числа 1 ко всем числам строки или столбца. Докажите, что A=B тогда и только тогда, когда p - простое.
7. В середине одной из стен квадратной комнаты 3*3 имеется проход шириной 1 (рисунок 1). Можно ли в эту комнату внести какой-нибудь стол, имеющий площадь более 4?
 |
| Рис. 1 |
8. Пусть [a, b, c] - наименьшее общее
кратное натуральных чисел a, b и c. Может ли для
каких-нибудь x, y и z оказаться, что
[x, y, z] = [x+1, y+1, z+1] =
[x+2, y+2, z+2]?