Рисунок 1.
В этом цикле задач мы предлагаем читателю выяснить связи между различными свойствами "узости" деревьев на плоскости. Наиболее интересные и нетривиальные из этих связей -
Теорема 1. Предположим, что K - подмножество плоскости и a - вектор, такие что KЗ(K+a)=Ж (через K+a обозначим образ множества K при сдвиге на вектор a). Тогда два воза (т. е. круга диаметра |a|) не могут поменяться местами при непрерывном движении их центров по K, так что возы не сталкиваются.
Теорема 2. Для любого e>0 существуют ограниченное подмножество плоскости K и вектор a, такие что KЗ(K+a)=Ж, |a|<e$, но ни для какого n множество K нельзя покрыть n плоскими многоугольниками C1, C2, ..., Cn диаметров меньше 1, такими что Ci пересекается только с Ci-1 и Ci+1 при каждом i=2, 3, ..., n-1.
Введем необходимые определения и соглашения. Если условие задачи является формулировкой утверждения, то его требуется доказать.
Дугой называется ломаная линия без самопересечений на плоскости (концы ломаной принадлежат ломаной).
Объединение дуг называется связным, если из любой его точки можно пройти в любую другую, двигаясь по этим дугам.
Деревом называется связное объединение дуг, не содержащее замкнутых ломаных.
Для подмножества K точек плоскости и вектора a через K+a будем обозначать образ множества K при параллельном переносе на вектор a.
Будем обозначать через |X,Y| расстояние между точками X, Y.
Для ломаной z и точки X минимум расстояний от точки X до точек ломаной называется расстоянием от точки X до ломаной z и обозначается |X,z|.
Знаменитая теорема Р. Л. Мура утверждает невозможность расположения на плоскости несчетного семейства попарно непересекающихся (гомеоморфных) копий буквы T (триода). Для случая, когда эти копии равны стандартной букве T (т. е. переводятся в нее некоторым движением), это - известная олимпиадная задача. После появления теоремы Мура стали активно изучаться атриодичные континуумы. Графским аналогом свойства атриодичности является свойство графа не содержать e-триода.
Определение 1.0. e-триодом называется объединение трех дуг AO, BO, CO, попарно не имеющих общих точек (кроме их общей вершины O), такое что |A,BOUCO|>e, |B,COUAO|>e, |C,AOUBO|>e.
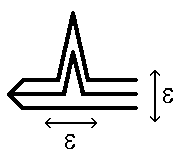
Задача 1.0. Дерево на рис. 1 не содержит e-триода (расстояние между "пиками" равно 1 и много больше e).

Рисунок 1.
Ясно, что возможность разместить в плоскости несчетное семейство попарно непересекающихся копий данного континуума характеризует его "узость". Графским аналогом (упрощенным) этого свойства "узости" является следующее свойство (которое кажется совсем не связанным с несчетными семействами!):
Определение 1.1. Дерево называется e-разводимым, если найдется такой вектор a длины меньше e, что KЗ(K+a)=Ж .
Это и все следующие вводимые свойства характеризуют "узость" графа, поскольку для них справедливы следующие утверждения.
Задача 1.1. Для каждого из понятий узости (определения 1.1-1.3)
a) Любая дуга e-узка для любого e (исключение состаляет e-разводимость: для любого e>0 нетрудно построить пример дуги, не являющейся e-разводимой. Попробуйте устранить этот недостаток, подправив определение e-разводимости).
b) e-триод не e-узок (начните со случая, когда AO, BO, CO - прямолинейные дуги).
c) Любое дерево, содержащееся в e-узком, само e-узко.
d) Никакое e-узкое дерево не содержит (в качестве подмножества) e-триода.
Предупреждение: доказать напрямую, что e-триод не e-разводим - трудно (лучше вывести это из теоремы 1).
Определение 1.2. Дерево K на плоскости называется симметрично e-стянутым, если никакие два воза (круга) диаметра e не могут поменяться местами при непрерывном движении их центров по K (возам запрещено сталкиваться).
Задача 1.2. Дерево на рис. 1 не является симметрично 1-стянутым.
Змеевидные континуумы стали активно изучаться после примера Р. Х. Бинга - основателя "техасской" топологической школы - однородного (змеевидного) континуума, отличного от окружности. Графским аналогом свойства змеевидности является следующее свойство:
Определение 1.3. Дерево K на плоскости называется e-змеевидным, если для некоторого n его можно покрыть n плоскими многоугольниками C1, C2, ..., Cn такими, что их диаметры меньше e и Ci пересекается только с Ci-1 и Ci+1 при i=2, 3, ..., n-1 .
Задача 1.3. Всякое e-змеевидное дерево симметрично e-стянуто (значит, дерево на рис. 1 не является e-змеевидным).
Задача 1.4. Докажите теорему 1 для случая, когда K - дерево на плоскости. (В наших определениях эту теорему можно переформулировать следующим образом: из e-разводимости следует симметричная e-стянутость).
Задача 1.5. Докажите теорему 2 (из e-разводимости не следует e-змеевидность).
Задача 1.6 формально не связана с остальными, но идеи ее решений могут оказаться полезными при размышлении над другими задачами этого цикла.
Задача 1.6. a) (Теорема о возах) Предположим, что два велосипедиста, связанные веревкой длины e, могут проехать по двум дорогам из A в B и из A' в B', соответственно. Тогда два воза (круга) диаметра e не смогут проехать из A в B и из B' в A', соответственно (ни в какой момент времени возы не могут пересекаться).
b) (Теорема об альпинистах) Два альпиниста стоят на уровне моря на противоположных сторонах горного хребта (плоской ломаной с конечным числом звеньев), расположенного целиком над уровнем моря. Тогда они могут встретиться, оставаясь в процессе движения все время на одной высоте над уровнем моря.
c) В единичном квадрате ABCD существуют 1000 ломаных L1, ..., L1000, соединяющих точки X1, ..., X1000 на стороне AB с точками Y1, ..., Y1000 на стороне CD со следующим свойством: для любых двух ломаных Li и Lj (i не равно j) два воза диаметра 1/10 смогут проехать из Xi в Yi и из Yj в Xj, соответственно (ни в какой момент времени возы не могут сталкиваться).
Среди предлагаемых задач есть нерешенные. Они помечены звёздочкой. Введём 3 новых понятия, связанных с узостью дерева. Диаграмму зависимости между всеми 6 понятиями смотрите после условий задач.
Задача 2.1. Решите задачу 1.1 для трёх новых свойств (определения 2.1-2.3).
Определение 2.1. Дерево K на плоскости называется e-стянутым, если никакие два e-воза не могут непрерывно двигаться по K так, чтобы их центры замели один и тот же след (как обычно, возам запрещено пересекаться).
Задача 2.2.
a) Всякое e-стянутое дерево симметрично
e-стянуто.
b)* Всякое ли симметрично e-стянутое
дерево e-стянуто?
Для любых X,Y C K, расстояние между которыми
больше e, определим отношение '<' (не
обязательно транзитивное, т. е. из A<B и B<C
может не следовать A<C). Для этого расположим двух человек
(люди, в отличие от возов - точки, а не круги) в точках X и
Y+a, соответственно. Будем двигать первого из них по
K из X в Y вдоль кратчайшей дуги l, а второго -
по K+a из Y+a в
X+a вдоль дуги l+a.
Если вектор, направленный от первого человека ко второму, повернулся по
часовой стрелке, то положим X<Y, а если против - положим
Y<X. Проверьте, что это отношение действительно определено
для любых точек X,Y C K, расстояние между
которыми больше e (т. е. вектор обязательно
повернётся, а не останется на месте). Покажитье также, что это отношение
непрерывно зависит от точек X,Y. Отсуда можно вывести решение
задачи 1.4. Эту же идею можно использовать для получения следующего более
сильного результата.
Задача 2.3.
a) Всякое дерево L, содержащееся в
e-разводимом дереве K, имеет
'<'-минимальную точку (Т. е. точку UCL, такую что
U<X, если точка XCL и
|X,U|>e).
b) Любое e-разводимое
дерево e-стянуто.
Дадим теперь подправленное определение e-разводимости (см. замечание в задаче 1.1.a).
Определение 2.2. Предположим, что дерево K разбито точками A1, A2, ..., An на отрезки. Перенесём каждую из этих точек на свой вектор длины меньше e, при этом получим новые точки A'1, A'2, ..., A'n. Соединим отрезком точки A'i, A'j в том и только в том случае, если в дереве K были соединены Ai, Aj. Если вновь проведённые отрезки образовали дерево (т. е. не возникло циклов), будем называть его e-деформацией дерева K. Дерево K на плоскости называется e-деформируемым, если оно не имеет общих точек с некоторой своей e-деформацией.
Можно показать, что всякое e-змеевидное дерево e-деформируемо. Проверьте, что приведённое указание к задаче 1.4. позволяет решить эту задачу и в предположении e-деформируемости дерева.
Задача 2.4. Всякое ли e-деформируемое
дерево
a)* e-стянутои ?
b)* диаметра 1 является e-змеевидным ?
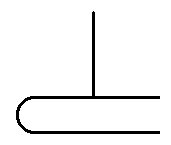
Рисунок 2.
Определение 2.3. Дерево K на плоскости называется e-зажатым, если для любого дерева LcK найдётся такая дуга lcL, что |X,l|<e для всех XcL.
В определении 2.3 условие LcK нельзя заменить на условие
L=K : для любого e>0 существует
дерево K (рис. 2), не являющееся
e-зажатым, но в котором найдётся такая дуга l,
что |X,l|<e для любой точки
XCK.
Задача 2.5. Дерево на рис. 1 является e-зажатым (значит, по задаче 1.3, из e-зажатости не следует симметричная 1-стянутость).
Задача 2.6. Является ли e-зажатым
a) всякое e-змеевидное дерево?
b) всякое e-разводимое дерево?
c)* всякое дерево, не содержащее
e-триодов?
d)* всякое e-стянутое
(симметрично e-стянутое) дерево?
Попытайтесь выяснить, верны ли утверждения задач 2.6.cd и других нерешённых задач, если в их заключениях мы поменяем e на 100e или на Me, где M - некоторая константа (при этом мы получим формально более слабые утверждения). Верно ли, например, что всякое дерево, не содержащее e-триодов, является 100e-зажатым?
