13-й Математический Праздник.
17 февраля 2002 года

Условия и решения задач.

6 класс

Задача 1 [3 балла].
Решите ребус: БАО*БА*Б=2002.
Авторы: А. Блинков, А. Хачатурян
Решение:
Если Б>2, то БА>20 и БАО>200, так что БАО*БА*Б>200*20*2=8000>2002. Значит, Б=1.
  Разложим число 2002 на простые множители: 2002=2*7*11*13. Теперь легко выписать все двузначные делители числа 2002, начинающиеся на цифру 1. Это числа 11, 13 и 2*7=14. Вычислим соответствующие частные: 2002:11=182, 2002:13=154 и 2002:14=143.
Ответ:143*14*1=2002.

Задача 2 [4 балла].
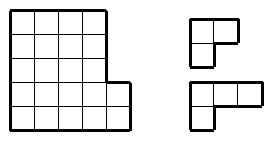
Незнайка разрезал фигуру на трёхклеточные и четырёхклеточные уголки, нарисованные справа от неё. Сколько трёхклеточных уголков могло получиться?
Автор: А. Митягин

Решение:
Фигура состоит из 22 клеток. Если при разрезании получилось x трёхклеточных уголков и y четырёхклеточных, то 3x+4y=22.
  Очевидно, что число x чётно и x<8 (3*8=24), так что x может быть равно 0, 2, 4 или 6. Ни 0, ни 4 не подходят: y должно быть целым. При x=2 получаем y=4, а при x=6 получаем y=1.
  Оба случая возможны, как показано на рисунках:

x=2		x=6

Ответ: 2 или 6.

Задача 3 [6 баллов].
На доске были написаны 10 последовательных натуральных чисел. Когда стёрли одно из них, то сумма девяти оставшихся оказалась равна 2002. Какие числа остались на доске?
Автор: В. Произволов
Решение
Обозначим наименьшее из десяти чисел буквой x. Тогда

x+(x+1)+(x+2)+(x+3)+(x+4)+(x+5)+(x+6)+(x+7)+(x+8)+(x+9)-(x+y)=2002,

10x+45-x-y=2002<\P>, то есть 9x=1957+y. Сумма 1957+y должна делиться на 9, а учитывая условие 0<y<9, получаем, что y=5. Значит, x=1962:9=218
Ответ:218, 219, 220, 221, 222, 224, 225, 226 и 227.

Задача 4.
Художник-авангардист Змий Клеточкин покрасил несколько клеток доски размером 7*7, соблюдая правило: каждая следующая закрашиваемая клетка должна соседствовать по стороне с предыдущей закрашенной клеткой, но не должна - ни с одной другой ранее закрашенной клеткой. Ему удалось покрасить 31 клетку.

Побейте его рекорд - закрасьте
а) 32 клетки - [2 балла];
б) 33 клетки - [3 балла].
Автор: И. Акулич
Решение:
Если мы умеем закрашивать 33 клетки, то 32 клетки можно закрасить, вовремя остановившись. Три примера, в которых закрашены 33 клетки, изображены на рисунке (на самом деле, таких примеров гораздо больше). Больше 33 клеток закрасить нельзя - это проверено на компьютере.

Задача 5 [6 баллов].
Илье Муромцу, Добрыне Никитичу и Алёше Поповичу за верную службу дали 6 монет: 3 золотых и 3 серебряных. Каждому досталось по две монеты. Илья Муромец не знает, какие монеты достались Добрыне, а какие Алёше, но знает, какие монеты достались ему самому. Придумайте вопрос, на который Илья Муромец ответит "да", "нет" или "не знаю", и по ответу на который Вы сможете понять, какие монеты ему достались.
Автор: А. Чеботарёв
Решение:
Вот пример такого вопроса:
"Правда ли, что у тебя золотых монет больше, чем у Алёши Поповича?"
Если у Ильи Муромца две золотые монеты, он скажет "да", поскольку у Алёши Поповича не может быть больше одной золотой монеты.
Если обе монеты Ильи серебряные, то у Алёши хотя бы одна золотая, и Илья Муромец ответит "нет".
Ну а если ему достались разные монеты, то он ответит "не знаю", так как у Алёши может оказаться как две золотые, так и две серебряные монеты.
  Конечно, можно было задать и другие вопросы, например:
- Правда ли, что одному из двух других богатырей достались две серебряные монеты?
- Верно ли, что два других богатыря получили хотя бы по одной золотой монете каждый?
- Если я заберу у тебя одну монету и дам вместо неё золотую, станет ли у тебя больше золотых?
(Заметьте, что в последнем вопросе не упоминаются монеты двух других богатырей, а только монеты, доставшиеся Илье Муромцу!)

Задача 6 [8 баллов].
Айрат выписал подряд все числа месяца:

123456789101112...