|
||||||||||
|
|
14-й Математический Праздник.
16 февраля 2003 года
Условия и решения задач.
6 класс
Задача 1. [4 балла]
Один мальчик 16 февраля 2003 года сказал: "Разность между числами
прожитых мною месяцев и прожитых (полных) лет сегодня впервые стала
равна 111". Когда он родился?
Ответ. 16 января 1993 года.
Решение. Пусть мальчик прожил x лет и еще
y месяцев. Тогда он прожил всего 12x+y месяцев и поэтому
то есть
Поскольку y<12, то y=1 и x=10.
Задача 2. [4 балла]
Найдите наименьшее четырехзначное число СЕЕМ,
для которого существует решение ребуса
МЫ + РОЖЬ = СЕЕМ.
(Одинаковым буквам соответствуют одинаковые цифры, разным — разные.
Ответ. 2003
Решение.
Поскольку С>Р, С>1. Так как мы ищем наименьшее
число, попробуем взять
Р=1, С=2 и Е=0. Тогда М>3. Случай
СЕЕМ=2003 возможен: 35+1968=2003 или 38+1965=2003.
Кроме указанных решений, ребус, как легко проверить при помощи
компьютерной программы, имеет еще 38 решений:
31+4972=5003, 32+4971=5003, 31+5972=6003, 32+5971=6003, 81+3927=4008, 87+3921=4008, 61+2945=3006, 65+2941=3006, 81+4927=5008, 14+2987=3001, 17+2984=3001, 87+4921=5008, 15+2986=3001, 16+2985=3001, 81+5927=6008, 87+5921=6008, 41+7963=8004, 71+4936=5007, 43+7961=8004, 76+4931=5007, 15+3986=4001, 16+3985=4001, 61+7945=8006, 65+7941=8006, 46+1958=2004, 48+1956=2004, 14+5987=6001, 17+5984=6001, 57+1948=2005, 58+1947=2005, 83+6925=7008, 85+6923=7008, 46+2958=3004, 48+2956=3004, 24+5978=6002, 57+2948=3005, 28+5974=6002, 58+2947=3005.
Задача 3. [4 балла]
На острове живут рыцари, которые всегда говорят правду, и лжецы,
которые всегда лгут. Путник встретил троих островитян и спросил каждого из
них: "Сколько рыцарей среди твоих спутников?". Первый ответил:
"Ни одного". Второй сказал: "Один". Что сказал третий?
Ответ. Один.
Решение.
Если первый — рыцарь, то в силу его слов второй и третий — лжецы,
что невозможно из-за высказывания второго островитянина. Значит,
первый — лжец. Если второй — лжец, то в силу его слов третий тоже лжец,
но тогда первый сказал правду, а он должен был соврать. Значит, второй —
рыцарь. В силу его слов третий тоже рыцарь.
Третий честно ответит: "Один".
Задача 4. [5 баллов]
Прямоугольник разрезан на несколько прямоугольников,
периметр каждого из которых — целое число метров. Верно
ли, что периметр исходного прямоугольника — тоже целое
число метров?
Ответ. Нет.
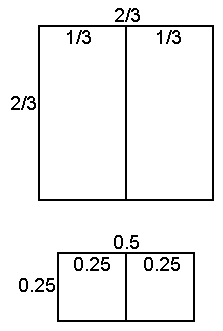
Решение. Например, квадрат со стороной 2/3 можно разрезать
средней линией на два прямоугольника, периметры которых равны 2.
Есть и другие примеры.
Задача 5. [7 баллов]
В распоряжении юного паркетчика имеются 10 одинаковых
плиток, каждая из которых состоит из 4 квадратов и имеет форму
буквы Г (все плитки ориентированы одинаково). Может ли он составить из них
прямоугольник размером 5*8? (Плитки можно поворачивать, но нельзя
переворачивать. Например, на рисунке изображено неверное решение:
заштрихованная плитка неправильно ориентирована.)
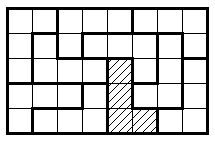
Ответ. Да, можно:

Задача 6. [8 баллов]
На гранях кубика расставлены числа от 1 до 6.
Кубик бросили два раза. В первый раз сумма чисел на четырех боковых
гранях оказалась равна 12, во второй — 15.
Какое число написано на грани, противоположной той, где написана цифра 3?
Ответ. 6.
Решение. Поскольку 1+2+3+4+5+6=21 и 21-12=9, а 21-15=6, то
в первый раз сумма чисел нижней и верхней граней кубика
равнялась 9, а во второй — 6. Бросим кубик третий раз так,
чтобы он упал на одну из тех двух граней, которые оба раза были
боковыми. Поскольку 21-9-6=6, то сумма чисел, которые при
третьем броске оказались на верхней и нижней гранях, равна 6.
Очевидно, цифра 3 не могла ни во второй, ни в третий раз оказаться на
верхней или нижней грани: иначе напротив нее стояла бы цифра 6-3=3,
а тройка только одна. Значит, тройка была на верхней или нижней грани при
первом броске. Поэтому напротив тройки стоит цифра 9-3=6.
Примечание. Удовлетворяющий условию задачи кубик
существует: 1+5=2+4=6 и 3+6=9.
Другое решение.
Если явно выписать все возможные сочетания чисел, которые могли
бы оказаться на боковых гранях при бросании такого кубика
(а таких сочетаний всего 15), то можно заметить, что и 12, и 15
в сумме набирается ровно двумя способами.
(12=1+2+3+6=1+2+4+5 15=2+3+4+6=1+3+5+6)
Легко заметить, что если бы 12 "выпало", как 1—2—3—6,
то при втором броске 15 получить было бы невозможно, так как на двух боковых гранях
было бы 4 и 5,
а сочетания с суммой 15, содержащего оба эти числа нет.
Значит, 12 "выпало" как 1—2—4—5. Следовательно,
напротив тройки написана шестерка.
Стоит еще показать, что такой кубик вообще существует.
Например, годится кубик на котором на противоположных гранях
написаны числа 1—5, 2—4 и 3—6 соответственно.
Авторское решение.
Заметим, что сумма всех чисел, написанных на кубике, равна 21.
Сумма чисел на верхней и нижней грани равна в 1-м и 2-м случаях 9 и 6
соответственно.
Из 1-го броска следует, что либо 3 напротив 6, либо 4 напротив 5.
Предположим, что 4 напротив 5.
Но из 2-го броска следует, что либо 1 напротив 5,
либо 2 напротив 4.
Противоречие, следовательно, 3 напротив 6.
Стоит еще показать, что такой кубик вообще существует.
Например, годится кубик на котором на противоположных гранях написаны
числа 1—5, 2—4 и 3—6 соответственно.
Дата последнего изменения — 17 февраля 2003 года







