Окружной тур.
Окружной тур для 5-7 классов проводился по школам (его могла организовать у себя любая школа). Рекомендованная оргкомитетом дата проведения этого мероприятия - 26 января 2002 г.
Окружной тур для 8-11 классах во всех московских округах, кроме Центрального, проводился 3 февраля 2002 года В Центральном округе олимпиада прошла 2 февраля по другим заданиям.
По московским заданиям олимпиада также была проведена и в некоторых других городах.
5 класс | 6 класс | 7 класс | 8 класс | 9 класс | 10 класс | 11 класс
Центральный округ: 8 класс | 9 класс | 10 класс | 11 класс
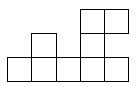
1. Даны четыре одинаковые фигуры (такие, как на рисунке).
Покажите, как из этих фигур сложить квадрат.

2. На двух чашах весов стояли 24 гири: на левой чаше - пятикилограммовые, а на правой - трёхкилограммовые. Весы находились в равновесии. Сколько гирь могло быть на каждой чаше?
3. Алёша пошёл в магазин и потратил половину имевшихся денег на молоко и сыр. Доехав на автобусе за 3 рубля до книжного магазина, он купил книгу. На неё он потратил половину оставшихся денег и ещё 1 рубль. Подсчитав оставшиеся деньги, Алёша половину из них истратил на тетради, а 4 рубля - на мороженое. В итоге у него осталось 3 рубля на обратный билет. Сколько всего денег было у Алёши?
4. В двузначном числе зачеркнули цифру, и оно уменьшилось в 46 раз. Определите, какое это было число и какую цифру зачеркнули.
5. Треугольник, квадрат, круг и пятиугольник выложили
в ряд. Цвета этих фигур различны. Красная фигура
лежит между зелёной и синей. Справа от жёлтой фигуры
лежит пятиугольник. Круг лежит правее, чем треугольник, и
правее, чем пятиугольник. Треугольник лежит не с краю.
Синяя фигура не лежит рядом с жёлтой.
Нарисуйте, как лежат данные фигуры, указав их цвета.
1. В некоторых клетках квадрата 4*4 расставлены буквы
a, b, c и d (смотри рисунок).
Заполните теми же буквами остальные клетки так, чтобы в каждом столбце
и в каждой строке каждая буква встречалась ровно один раз.
6 класс
| a | |||
| b | |||
| c | |||
| d |
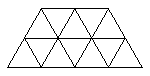
2. Разрежьте фигуру, изображённую на рисунке, на 4 равные части
(одинаковые по форме и по размеру).
3. В бак, имеющий форму куба, выливают ведро воды (10 литров). Каков будет уровень воды в баке, если ребро куба имеет длину 1 метр?
4. Волк и Заяц устроили забег на стадионе. Встав рядом, они одновременно стартовали в одном направлении. Известно, что скорость Волка в 2 раза больше скорости Зайца. Сколько кругов успеет пробежать Заяц до тех пор, пока его снова не догонит Волк?
5. Винни-Пух и Пятачок играют в слова. Винни-Пух придумал 10 слов,
а Пятачок - только 5. Они по очереди называют по одному слову, не повторяя уже
названные. Проигрывает тот, кто не сможет назвать слово. Начинал Винни-Пух,
а выиграл Пятачок. Придумайте за них слова и укажите, в каком порядке
они могли их называть.
1. Числитель дроби увеличили на 3, а знаменатель - на 8.
Могла ли получиться дробь, равная исходной? Ответ обоснуйте.
2. На стороне AC треугольника АВС отметили точку
Е. Известно, что периметр треугольника АВС равен 25 см,
периметр треугольника АВЕ - 15 см, а периметр
треугольника ВСЕ - 17 см. Найдите длину отрезка ВЕ.
3. Решите уравнение (|x|-x)/(x-1)=0
4. В городе Глупове живут только полицейские, воры и обыватели.
Полицейские всегда врут обывателям, воры - полицейским, а обыватели - ворам.
Во всех остальных случаях жители Глупова говорят правду.
Однажды несколько глуповцев водили хоровод и каждый сказал своему правому
соседу: "Я - полицейский". Сколько обывателей было в этом хороводе?
5. В мешке у Деда Мороза лежат конфеты трёх видов: шоколадные,
ириски и леденцы. Дед Мороз знает, что если вынуть любые 100 конфет из мешка,
то среди них обязательно найдутся конфеты всех трёх видов.
Какое наибольшее количество конфет может быть в мешке у Деда Мороза?
1. От причала A к причалу B отошли катер и лодка.
Известно, что они плыли с постоянными скоростями, причём скорость катера была
в 5 раз больше, чем скорость лодки, но катер сделал несколько остановок.
Сколько времени катер затратил на остановки, если на путь от A до
B он затратил 2 часа, а лодка - 4 часа?
2. Решите уравнение
x3+5x2+2x=8
3. В выпуклом четырёхугольнике ABCD
точки M и N - середины сторон AB и CD
соответственно. Известно, что MN=(AD+BC)/2.
Верно ли, что AD||BC ?
5. На острове живут только рыцари (которые всегда говорят правду)
и лжецы (которые всегда лгут).
7 класс
8 класс
Трое из них сделали по два заявления.
| Первый сказал: | "На острове живёт не более 3 человек" |
| "Все жители острова - лжецы" | |
| Второй сказал: | "На острове живёт не более 4 человек" |
| "Не все жители острова - лжецы" | |
| Третий сказал: | "На острове живёт 5 человек" |
| "На острове не менее 3 лжецов" |
6. В треугольнике ABC высоты AA1 и
CC1 пересекаются в точке H, лежащей внутри
треугольника. Известно, что H - середина AA1,
а CH:HC1=2:1.
Найдите величину угла B.
7. У Васи было 20 настоящих монет и 21 фальшивая.
Каждая фальшивая монета на 1 грамм легче настоящей.
Одну монету Вася потерял.
Есть чашечные весы, которые показывают, на сколько грамм
одна чаша перевешивает другую.
Как определить за одно взвешивание, какая монета потерялась?
1. Из пункта A в пункт B одновременно выехали
"Мерседес" и "Запорожец". Проехав треть пути, "Запорожец" остановился
и тронулся с места только тогда, когда "Мерседесу" оставалось проехать треть
пути до B. Доехав до B, "Мерседес" развернулся и поехал обратно
в A. Какой из автомобилей приедет раньше: "Мерседес" - в пункт
A или "Запорожец" - в пункт B ?
2. Числа x и y положительны, x+y=6.
Найдите наименьшее возможное значение суммы (1/x)+(1/y) .
3. Дано два непересекающихся круга. Существует ли вне
этих кругов такая точка, что всякая прямая, проходящая через неё, пересекает
хотя бы один из данных кругов?
4. Оля и Коля играют на доске размером 9*9 клеток.
Первым ходом Оля закрашивает произвольную неугловую клетку.
Далее игроки по очереди закрашивают по одной клетке, примыкающей к любой из
уже закрашенных. Побеждает тот, кто первым закрасит одну из угловых клеток.
Кто выиграет при правильной игре и как он должен играть?
5. Через точку пересечения медиан треугольника ABC
проходит прямая, пересекающая стороны AB и AC.
Расстояния от вершин B и C до этой прямой равны
b и c соответственно. Найдите расстояние от вершины
A до данной прямой.
6. Сравните числа A и B, не пользуясь калькулятором:
1. Постройте график уравнения
2. Известно, что положительное число a является
одним из корней уравнения
3. Основания трапеции равны 3 см и 5 см.
Одна из диагоналей трапеции равна 8 см, угол между диагоналями
равен 60o. Найдите периметр трапеции.
5. Сколько пар (x, y) целых чисел
являются решениями уравнения
6. Отрезок АВ длиной 8 см лежит в плоскости
a. Точка М находится на расстоянии 10 см
от ближайшей к ней точки отрезка АВ и на расстоянии 6 см от
плоскости a. Точка O - проекция точки М
на плоскость a. Найдите площадь треугольника
АОВ, если известно, что один из углов этого треугольника равен
150o.
7. Один математик говорит другому: "Я думаю, ты сможешь узнать,
сколько у меня внуков и сколько лет исполнилось каждому, если я
сообщу тебе, что произведение их возрастов равно 36, а сумма - количеству
этажей в доме напротив".
1. Решите уравнение
2. Существует ли многогранник, у которого ровно 13 рёбер?
3. Что больше:
4. Из вершин C и D ромба ABCD с острым
углом A на прямую AB опущены перпендикуляры CQ и
DP. Точки M и N - середины отрезков PB и
CQ соответственно.
Докажите, что AN | DM .
5. В траншею, имеющую в сечении форму параболы
y=x2, требуется уложить трубу круглого сечения
так, чтобы она касалась дна траншеи. При каком наибольшем радиусе трубы
это возможно?
6. Докажите неравенство
1. В клетках прямоугольной таблицы 2001 на 2002 записаны некоторые
числа, причем сумма чисел в любом столбце или строке одинакова. Найти эту
сумму.
2. Три целых x, y и z числа удовлетворяют
уравнению x2+y2=z2.
Доказать, что одно из них четное.
3. Оля и Коля играют на доске размером 9*9 клеток. Первым ходом
Оля закрашивает произвольную неугловую клетку. Далее игроки по очереди
закрашивают по одной клетке, примыкающей к любой из уже закрашенных.
Побеждает тот, кто первым закрасит одну из угловых клеток. Кто выиграет при
правильной игре и как он должен играть?
4. Может ли целое число, являющееся квадратом другого целого числа,
состоять только из цифр 0 и 6?
5. В треугольнике АВС высоты АА1 и
СС1 пересекаются в точке Н, лежащей внутри
треугольника. Известно, что Н - середина АА1,
а СН:НС1=2:1. Найдите величину угла В.
6. У Васи было 20 настоящих монет и 21 фальшивая. Каждая фальшивая
монета на 1 грамм легче настоящей. Одну монету Вася потерял. Есть чашечные
весы, которые показывают, на сколько грамм одна чаша перевешивает другую.
Как определить за одно взвешивание, какая монета потерялась?
1. Существует ли простое число р, такое что число
3р+2001 тоже простое?
2. Решить неравенство
3. Дано два непересекающихся круга. Существует ли вне этих кругов
такая точка, что всякая прямая, проходящая через неё, пересекает хотя бы один
из данных кругов?
4. На острове живут только рыцари (которые всегда говорят правду)
и лжецы (которые всегда лгут). Трое из них сделали по два заявления.
9 класс
A=1-51/3+251/3
B=31/3-91/3+151/3
10 класс
|y|=(1 - cos2 x)1/2/(sin x)
x(x+1)(x+2)...(x+100)=1 .
Докажите, что a<1/(100!) .
(Напомним, что n!=1*2*3*...*(n-1)*n)
(х2 + х + 1)2 + (y2 - y + 1)2 = 20022 ?
"Этой информации не достаточно!" - возражает второй.
Тогда первый добавляет: "Старшего внука зовут Вася".
"Теперь другое дело!" - говорит второй и даёт
правильный ответ. Дайте его и вы. Объясните.
11 класс
((2+x)1/2+(2-x)1/2)/((2+x)1/2-(2-x)1/2)=2/x
2001 + sin 2001 или 2002 + sin 2002 ?
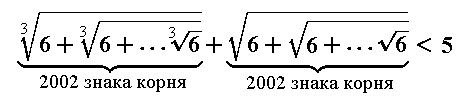
8 класс (Центральный округ)
9 класс (Центральный округ)
x10+x6+x5+x3+x2+x+1>0
| Первый сказал: | "На острове живёт не более 3 человек" |
| "Все жители острова - лжецы" | |
| Второй сказал: | "На острове живёт не более 4 человек" |
| "Не все жители острова - лжецы" | |
| Третий сказал: | "На острове живёт 5 человек" |
| "На острове не менее 3 лжецов" |
5. В прямоугольном треугольнике АВС на гипотенузу опущена высота CD. Доказать, что сумма длин радиусов окружностей, вписанных в треугольники ABC, ACD и CBD равна длине CD.
6. Составьте из бесконечного набора чисел
1. Постройте график уравнения
2. Существует ли треугольник длины высот которого равны
числам 1; 2 и 3?
3. Двузначное число, у которого число единиц больше числа десятков
умножили на 9. Найти сумму цифр полученного числа.
4. Сравнить два числа (sin 1)/(sin 2) и (sin 2)/(sin 3) .
5. Через точку пересечения медиан треугольника АВС проходит
прямая, пересекающая стороны АВ и АС. Расстояния от вершин
В и С до этой прямой равны b и с соответственно.
Найдите расстояние от вершины А до данной прямой.
6. Существуют ли натуральные числа x и y,
при которых выражение
1. Решите уравнение
2. Из вершин С и D ромба АВСD с острым углом
А на прямую АВ опущены перпендикуляры СQ и DР.
Точки М и N - середины отрезков РВ и СQ
соответственно. Докажите, что АN | DM.
3. Написано несколько положительных чисел, каждое из которых равно
полусумме остальных. Сколько написано чисел?
4. Центры двух единичных кубов совпадают. Доказать, что при любом
взаимном положении объем общей части не меньше p/6.
5. В траншею, имеющую в сечении форму параболы
у=x2, требуется уложить трубу круглого сечения так,
чтобы она касалась дна траншеи. При каком наибольшем радиусе трубы это
возможно?
6. Найти непрерывную на R функцию, такую, что для любых
x
2-1, 2-2, ..., 2-n, ...
геометрическую прогрессию, сумма которой будет равна 1/7.
Ответ обосновать.
10 класс (Центральный округ)
|y|=(1 - cos2 x)1/2/(sin x)
2x2+3xy+y2
принимает значение 32002 ?
11 класс
((2+x)1/2+(2-x)1/2)/((2+x)1/2-(2-x)1/2)=2/x
C R, y C R
справедливы равенства
f(x+y)=f(x)+f(y)+xy
и f(1)=1 .