65 Московская математическая олимпиада

Условия и решения задач 11 класса

1. Тангенсы углов треугольника - натуральные числа. Чему они могут быть равны.
(А. Заславский)

Ответ: Тангенсы углов треугольника равны 1, 2 и 3.

Решение. Смотрите решение задачи 10.1

2. Докажите, что на графике функции y=x³ можно отметить такую точку A, а на графике функции y=x³+|x|+1 - такую точку B, что расстояние AB не превышает 1/100.
(А. Спивак, А. Хачатурян)

Решение. Положим t=100. Точка B с координатами (t, c), где c=t³+t+1, очевидно, лежит на графике функции y=x³+|x|+1.

Рассмотрим положительное число r=c^1/3-t. Тогда (t+r)³=c, следовательно, точка A с координатами (t+r, c) лежит на графике функции y=x³.

Расстояние между точками A и B равно r. Но из равенства (t+r)³=c=t³+t+1 следует, что 3t²r+3tr²+r³=t+1, 3t²r<t+1, r<(t+1)/(3t²)=101/(3*100*100)<1/100.

3. Каждый зритель, купивший билет в первый ряд кинотеатра, занял одно из мест в первом ряду. Оказалось, что все места в первом ряду заняты, но каждый зритель сидит не на своём месте. Билетёр может менять местами соседей, если оба сидят не на своих местах. Всегда ли он может рассадить всех на свои места?
(А. Шаповалов)

Ответ: всегда.

Решение. Смотрите решение задачи 10.4

4. В возрастающей последовательности натуральных чисел каждое число, начиная с 2002-го, является делителем суммы всех предыдущих чисел. Докажите, что в последовательности найдётся некоторое число, начиная с которого каждое число равно сумме всех предыдущих.
(А. Шаповалов)

Решение. Рассмотрим последовательность частных k_n, n>2002. Пусть частное от деления суммы S_n-1 предыдущих членов на очередной член a_n равно k_n, то есть S_n-1=a_nk_n. Так как следующий член a_n+1 делит сумму S_n-1+a_n и a_n+1>a_n, то
k_n+1=S_n/a_n+1=(S_n-1+a_n)/a_n+1<(S_n-1+a_n)/a_n=k_n+1.
То есть частные не возрастают: k_n+1<k_n. Поэтому, начиная с некоторого места (при n>N), k_n=k. Но тогда при n>N имеем a_n+1=(S_n-1+a_n)/k=a_n+(a_n/k), то есть с этого места получаем геометрическую прогрессию a_n+1=((k+1)/k)a_n=((k+1)^n-N)/(k^n-N))a_N. Получаем, что a_N делится на сколь угодно большую степень k. Значит, k=1, что и требовалось доказать.

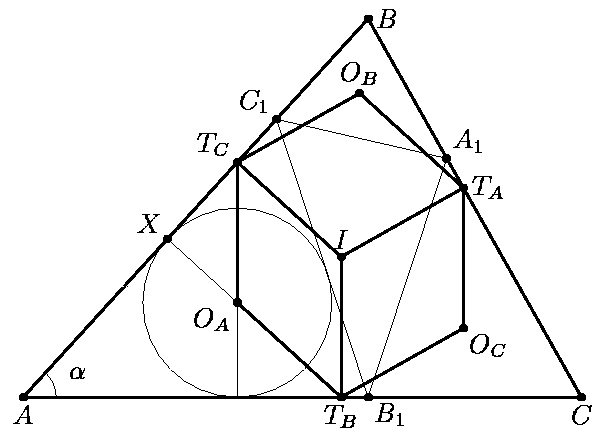
5. Пусть AA₁, BB₁, CC₁ - высоты остроугольного треугольника ABC; O_A, O_B, O_C центры вписанных окружностей треугольников AB₁C₁, BC₁A₁, CA₁B₁, соответственно; T_A, T_B, T_C - точки касания вписанной окружности треугольника ABC со сторонами BC, CA, AB соответственно. Докажите, что все стороны шестиугольника T_AO_CT_BO_AT_CO_B равны.
(Л. Емельянов)

Решение. Обозначим через I центр вписанной окружности треугольника ABC, а через r - её радиус. Пусть /BAC=a (см. рис.).

Докажем, что T_BO_A | AB. Находим
AB₁=AB cos a,\ AC₁=AC cos a.
В треугольниках BAC и B₁AC₁ угол BAC общий и
AB₁/AB=AC₁/AC=cos a.
Таким образом, треугольники B₁AC₁ и BAС подобны с коэффициентом подобия, равным cos a. Пусть X - проекция точки O_A на AB. Отрезки AX и AT_B - это отрезки от вершины A до точек касания соответствующих сторон со вписанной окружностью в подобных треугольниках B₁AC₁ и BAС, то есть AX и AT_B - соответственные элементы в подобных треугольниках. Поэтому AX=AT_B cos a. Но если Y - проекция точки T_B на AB, то AY=AT_B cos a. Это означает, что AX=AY, то есть точки X и Y совпадают. Отсюда следует, что T_BO_A | AB.

Аналогично приведённому выше рассуждению докажем, что
T_AO_B | AB, T_CO_B | BC, T_BO_C | BC, T_AO_C | CA, T_CO_A | CA.

Очевидно, IT_C | AB, IT_A | BC, IT_B | CA, а также IT_A=IT_B=IT_C=r. В четырёхугольнике T_BO_AT_CI противоположные стороны параллельны, следовательно, T_BO_AT_CI - параллелограмм, в котором
IT_B=IT_C=T_BO_A=T_CO_A=r.
Аналогично получаем, что
T_CO_B=T_AO_B=T_AO_C=T_BO_C=r,
таким образом, все стороны шестиугольника T_AO_CT_BO_AT_CO_B равны r.

Замечание. Из приведённого решения очевидно, что шестиугольник T_AO_CT_BO_AT_CO_B центрально-симметричен. Менее очевидно, что его центр симметрии лежит на прямой, соединяющей центры вписанной и описанной окружностей треугольника ABC. Читателю предлагается доказать эти утверждения самостоятельно.

6. В городе Удоеве выборы мэра проходят следующим образом. Если в очередном туре голосования никто из кандидатов не набрал больше половины голосов, то проводится следующий тур с участием всех кандидатов, кроме последнего по числу голосов. (Никогда два кандидата не набирают голосов поровну; если кандидат набрал больше половины голосов, то он становится мэром и выборы заканчиваются.) Каждый избиратель в каждом туре голосует за одного из кандидатов. Если это кандидат вышел в следующий тур, то избиратель снова голосует за него. Если же кандидат выбыл, то все его избиратели голосуют за одного и того же кандидата из числа оставшихся.
На очередных выборах баллотировалось 2002 кандидата. Мэром стал Остап Бендер, занявший в первом туре k-е место по числу голосов. Определите наибольшее возможное значение k, если Остап Бендер был избран
а) в 1002-м туре;
б) в 1001-м туре.
(Б. Френкин)

Ответ:
а) k=2001;
б) k=1.

Решение. Смотрите решение задачи 10.5 < /HTML>