9 класс
1. Хулиганы Джей и Боб на уроке черчения нарисовали головастиков (четыре окружности на рисунке - одного радиуса, треугольник - равносторонний, горизонтальная сторона этого треугольника - диаметр окружности). Какой из головастиков имеет бо'льшую площадь?
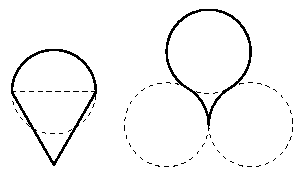
2. Произведение пяти чисел не равно нулю. Каждое из этих чисел уменьшили на единицу, при этом их произведение не изменилось. Приведите пример таких чисел.
3. В магазине три этажа, перемещаться между которыми можно только
на лифте. Исследование посещаемости этажей магазина показало, что с начала
рабочего дня и до закрытия магазина:
1) из покупателей, входящих в лифт на втором этаже, половина едет на
первый этаж, а половина - на третий;
2) среди покупателей, выходящих из лифта, меньше трети делает это на
третьем этаже.
На какой этаж покупатели чаще ездили с первого этажа, на второй или
на третий?
4. Есть шоколадка в форме равностороннего треугольника со стороной n, разделенная бороздками на равносторонние треугольники со стороной 1. Играют двое. За ход можно отломать от шоколадки треугольный кусок вдоль бороздки, съесть его, а остаток передать противнику. Тот, кто получит последний кусок - треугольник со стороной 1, - победитель. Тот, кто не может сделать ход, досрочно проигрывает. Кто выигрывает при правильной игре?
5. В окружность вписан прямоугольный треугольник АВС с гипотенузой АВ. Пусть K - середина дуги ВС, не содержащей точку А; N - середина отрезка АС, М - точка пересечения луча KN с окружностью. В точках А и С проведены касательные к окружности, которые пересекаются в точке Е. Докажите, что /ЕМK = 90o.
6. В тюрьму поместили 100 узников. Надзиратель сказал им:
"Я дам вам вечер поговорить друг с другом, а потом рассажу
по отдельным камерам, и общаться вы больше не сможете.
Иногда я буду одного из вас отводить в комнату, в которой есть лампа
(вначале она выключена). Уходя из комнаты, вы можете оставить лампу
как включенной, так и выключенной.
Если в какой-то момент кто-то из вас скажет мне, что вы все уже побывали в комнате, и будет прав, то я всех вас выпущу на свободу. А если неправ - скормлю всех крокодилам. И не волнуйтесь, что кого-нибудь забудут - если будете молчать, то все побываете в комнате, и ни для кого никакое посещение комнаты не станет последним."
Придумайте стратегию, гарантирующую узникам освобождение.
1. Существуют ли такие натуральные числа a, b
и c, что у каждого из уравнений
2. По рёбрам выпуклого многогранника с 2003 вершинами проведена
замкнутая ломаная, проходящая через каждую вершину ровно один раз.
Докажите, что в каждой из частей, на которые эта ломаная делит
поверхность многогранника, количество граней с нечётным числом сторон
нечётно.
3. Пусть P(x) - многочлен со старшим
коэффициентом 1, а последовательность целых чисел a1,
a2, ... такова, что P(a1)=0,
P(a2)=a1,
P(a3)=a2 и т. д.
Числа в последовательности не повторяются. Какую степень может иметь
P(x)?
4. Пусть M - точка пересечения медиан
в DABC. На перпендикулярах, опущенных из M
на стороны BC, AC и AB, взяты точки
A1, B1 и C1
соответственно, причём
A1B1 | MC и
A1C1 | MB.
Докажите, что M является точкой пересечения медиан и в
DA1B1C1.
5. В стране несколько городов, соединённых дорогами с односторонним
и двусторонним движением. Известно, что из каждого города в любой другой
можно проехать ровно одним путём, не проходящим два раза через один и тот
же город. Докажите, что страну можно разделить на три губернии так, чтобы ни
одна дорога не соединяла два города из одной губернии.
6. Дана бесконечная последовательность многочленов
P1(x), P2(x), ... .
Всегда ли существует конечный набор функций
f1(x), f2(x), ...,
fN(x), композициями которых можно
записать любой из них (например,
P1(x)=f2(f1(f2(x))))?
1. Для положительных чисел x, y, z
выполнено равенство
10 класс
ax2+bx+c=0,
ax2+bx-c=0,
ax2-bx+c=0,
ax2-bx-c=0
оба корня - целые?
11 класс