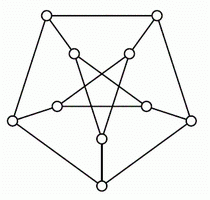
2. Можно ли покрасить 15 отрезков, изображенных на рисунке, в 3 цвета так, чтобы никакие 2 отрезка одного цвета не имели общего конца?
Олимпиада состоялась 4 марта 2007 года.
1. За первый год население некоторой деревни возросло на n человек, а за второй — на 300 человек. При этом за первый год население увеличилось на 300%, а за второй — на n%. Сколько жителей стало в деревне?
2. Дано натуральное число N. Для того, чтобы найти целое число, ближайшее к √ N, воспользуемся следующим способом: найдем среди квадратов натуральных чисел число a2, ближайшее к числу N; тогда a и будет искомым числом. Обязательно ли этот способ даст правильный ответ?
3. В футбольном чемпионате участвовали 16 команд. Каждая команда сыграла с каждой по одному разу, за победу давалось 3 очка, за ничью 1 очко, за поражение — 0. Назовем команду успешной, если она набрала хотя бы половину от наибольшего возможного количества очков. Какое наибольшее количество успешных команд могло быть в турнире?
4. В треугольник ABC с прямым углом C вписана окружность, касающаяся сторон AC, BC и AB в точках M, K и N соответственно. Через точку K провели прямую, перпендикулярную отрезку MN. Она пересекла катет AC в точке X. Докажите, что CK=AX.
5. Капитан Врунгель в своей каюте разложил перетасованную колоду из 52 карт по кругу, оставив одно место свободным. Матрос Фукс с палубы, не отходя от штурвала и не зная начальной раскладки, называет карту. Если эта карта лежит рядом со свободным местом, Врунгель ее туда передвигает, не сообщая Фуксу. Иначе ничего не происходит. Потом Фукс называет еще одну карту, и так сколько угодно раз, пока сам не скажет «стоп». Может ли Фукс добиться того, чтобы после «стопа» каждая карта наверняка оказалась не там, где была вначале?
6.
В выпуклом четырехугольнике ABCD стороны AB, BC и CD равны,
M — середина стороны AD. Известно, что угол BMC
равен 90о.
Найдите угол между диагоналями четырехугольника ABCD.
9 класс
1. Номер нынешней олимпиады (70) образован последними цифрами года ее проведения, записанными в обратном порядке. Сколько еще раз повторится такая ситуация в этом тысячелетии?
2. На параболе y=x2 выбраны четыре точки A, B, C, D так, что прямые AB и CD пересекаются на оси ординат. Найдите абсциссу точки D, если абсциссы точек A, B и C равны a, b и c соответственно.
3. Найдите все возрастающие конечные арифметические прогрессии, которые состоят из простых чисел и у которых количество членов больше, чем разность прогрессии.
4. Выпуклая фигура F обладает следующим свойством: любой правильный треугольник со стороной 1 можно параллельно перенести так, что все его вершины попадут на границу F. Обязательно ли F — круг? (Фигура называется выпуклой, если отрезок, соединяющий любые две ее точки, целиком лежит внутри фигуры.)
5. В однокруговом футбольном турнире играли n>4 команд. За победу давалось 3 очка, за ничью 1, за проигрыш 0. Оказалось, что все команды набрали поровну очков.
а) Докажите, что найдутся 4 команды, имеющие поровну побед, поровну ничьих и поровну поражений.
б) При каком наименьшем n могут не найтись 5 таких команд?
6.
Стороны треугольника ABC видны из точки T под углами
120o. Докажите, что прямые, симметричные прямым AT, BT и CT
относительно прямых BC, CA и AB соответственно, пересекаются в одной
точке.
10 класс
1. На сторонах единичного квадрата отметили точки K, L, M и N так, что прямая KM параллельна двум сторонам квадрата, а прямая LN — двум другим сторонам квадрата. Отрезок KL отсекает от квадрата треугольник периметра 1. Треугольник какой площади отсекает от квадрата отрезок MN?
|
2. Можно ли покрасить 15 отрезков, изображенных на рисунке, в 3 цвета так, чтобы никакие 2 отрезка одного цвета не имели общего конца? |

|
3. Существуют ли такие натуральные числа x и y, что x2+x+1 является натуральной степенью y, а y2+y+1 — натуральной степенью x?
4. Капитан Врунгель в своей каюте раскладывает пасьянс. Перетасованная колода из 52 карт разложена по кругу, одно место свободно. Матрос Фукс, не отходя от штурвала и не зная начальной раскладки, называет карту. Если эта карта лежит рядом со свободным местом, Врунгель передвигает ее на это место, не сообщая Фуксу. Иначе ничего не происходит. Потом Фукс называет еще одну карту, Врунгель совершает аналогичное действие, и так сколько угодно раз, пока Фукс не скажет «хватит». Фукс выиграет, если скажет «хватит» в тот момент, когда каждая карта окажется не на том месте, на котором была вначале. Может ли Фукс выиграть наверняка?
5. Треугольник ABC вписан в окружность с центром в O. X — произвольная точка внутри треугольника ABC, такая, что ∠XAB=∠XBC=φ, а P — такая точка, что PX⊥ OX, ∠XOP=φ, причем углы ∠XOP и ∠XAB одинаково ориентированы. Доказать, что все такие точки P лежат на одной прямой.
6.
С ненулевым числом разрешается проделывать
следующие операции:
1. Круглая мишень разбита на 20 секторов, которые нумеруются по кругу в каком-либо порядке числами 1, 2,…, 20. Если секторы занумерованы, например (как при игре в дартс), в следующем порядке 1, 20, 5, 12, 9, 14, 11, 8, 16, 7, 19, 3, 17, 2, 15, 10, 6, 13, 4, 18, то наименьшая из разностей между номерами соседних (по кругу) секторов равна 12–9=3 (из большего числа вычитается меньшее). Может ли указанная величина при нумерации в другом порядке быть больше 3? Каково наибольшее возможное значение этой величины?
2. Значение a подобрано так, что число корней первого из уравнений
| 4x-4-x=2cos ax, | 4x+4-x=2cos ax+4 |
3. Каким может быть произведение нескольких различных простых чисел, если оно кратно каждому из них, уменьшенному на 1? Найдите все возможные значения этого произведения.
Примечание. В распечатанных для участников олимпиады вариантах эта задача была сформулирована чуть иначе.3. Каким может быть произведение N нескольких различных простых чисел, если оно кратно каждому из них, уменьшенному на 1? Найдите все возможные значения N.Возникающая неточность понимания была специально откомментирована во всех аудиториях.
4. Точка O лежит в основании A1A2…An пирамиды SA1A2… An, причем SA1=SA2=…=SAn и ∠SA1O=∠SA2O=…=∠SAnO. При каком наименьшем значении n отсюда следует, что SO — высота пирамиды?
5. Квадрат состоит из n x n клеток: две противоположные угловые клетки — черные, а остальные — белые. Какое наименьшее количество белых клеток достаточно перекрасить в черный цвет, чтобы после этого с помощью преобразований, состоящих в перекрашивании всех клеток какого-либо столбца или какой-либо строки в противоположный цвет, можно было сделать черными все клетки этого квадрата?
6. Точки A', B' и C' — середины сторон BC, CA и AB треугольника ABC соответственно, а BH — его высота. Докажите, что если описанные около треугольников AHC' и CHA' окружности проходят через точку M, отличную от H, то ∠ABM=∠CBB'.
7. Миша мысленно расположил внутри данного круга единичного радиуса выпуклый многоугольник, содержащий центр круга, а Коля пытается угадать его периметр. За один шаг Коля указывает Мише какую-либо прямую и узнает от него, пересекает ли она многоугольник. Имеет ли Коля возможность наверняка угадать периметр многоугольника:
а) через 3 шага с точностью до 0,3;
б) через 2007 шагов с точностью до 0,003?