1.1. Вася перемножил квадрат и куб некоторого натурального числа, отличного от единицы. Мог ли он получить шестую степень какого-то натурального числа? Обоснуйте.

Ответ: мог, например, 64² × 64³ = 32⁶.

Так как , то равенство выполняется, если , , где – некоторое натуральное число. Возьмем, например, , тогда ; , то есть, .(2⁶)² × (2⁶)³ = (2⁵)⁶.

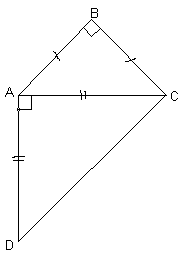
1.2. Известно, что треугольники АВС и ADC – прямоугольные равнобедренные. Следует ли из этого, что Ð АВС = Ð АDС?

1.3. Существует ли треугольник, градусная мера каждого угла которого выражается простым числом?

Ответ: да, существует, например, треугольник с углами: 2° , 11° и 167° .

Другие возможные примеры: 2° , 5° и 173° ; 2° , 29° и 149° ; 2° , 41° и 137° ; 2° , 47° и 131° ; 2° , 71° и 107° ; 2° , 89° и 89° .

2.1. Известно, что а = 3²⁰⁰⁴ + 2. Верно ли, что а² + 2 – простое число? Обоснуйте.

Заметим, что данное число при делении на 3 дает остаток 2, следовательно, оно имеет вид: , где t – некоторое натуральное число (в данном случае ). Тогда , то есть, кратно трем при любом натуральном t. Следовательно, это число не является простым.

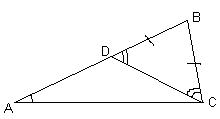
2.2. В треугольнике ABC угол С в три раза больше угла A. На стороне AB взята такая точка D, что BD = BC. Найдите CD, если AD = 4.

Ответ: CD = 4.

Пусть Ð BAC = a , тогда Ð BCA = 3a (см. рис. 2). Так как треугольник DBC – равнобедренный, то Ð BDC = Ð BCD = b . Тогда Ð DСA = 3a . – b . Так как Ð CDB – внешний для треугольника ADС, то Ð CDB = Ð DAC + Ð DСA. Следовательно, b = a + (3a . – b ) Û b = 2a .. Таким образом, Ð DСA = a , то есть, треугольник АDC – равнобедренный с основанием АС. Следовательно, СD = AD = 4.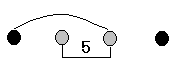

2.3. Существуют ли четыре числа, попарные разности между которыми равны: 2, 2, 3, 4, 5, 6? Обоснуйте.

Ответ: нет, не существуют.

2) рассмотрим два числа, разность между которыми равна 5. Если одно из них – «крайнее», то разность между вторым числом и другим «крайним» числом должна быть равна 1, тогда как в исходном наборе единицы не было. Если же равна пяти разность двух «средних» чисел, то разность между «крайним» и одним из средних чисел (на рис. 3 они соединены линией) должна быть больше пяти – противоречие.

3.1. Докажите, что если xy + z = yz + x = zx + y, то (x – y)(y – z)(z – x) = 0.

xy + z = yz + x Û xy – yz + z – x = 0 Û y(x – z) – (x – z) = 0 Û (x – z)(y – 1) = 0 Û x = z или y = 1. Аналогично, из равенства xy + z = zx + y можно получить, что y = z или x = 1, а из равенства yz + x = zx + y можно получить, что x = y или z = 1.

Заметим, что если выполняется хотя бы одно из равенств x = z; y = z или x = y, то равенство (x – y)(y – z)(z – x) = 0 также выполняется. Предположим, что это не так, то есть: x ¹ z, y ¹ z и x ¹ y, тогда x = 1, y = 1 и z = 1, следовательно, x = y = z – противоречие.

Таким образом, выполняется хотя бы одно из равенств x = z; y = z или x = y, следовательно, выполняется и доказываемое равенство.

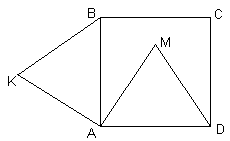
3.2. ABCD – квадрат. Треугольники АМD и AKB – равносторонние (см. рисунок). Верно ли, что точки С, М и K лежат на одной прямой?

Ответ: да, верно.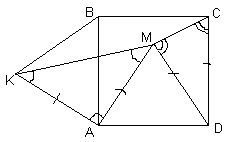

Проведем отрезки МK и MC и докажем, что Ð КМС – развернутый (см. рис. 4). Так как сторона каждого равностороннего треугольника равна стороне квадрата, то треугольники КАМ и MDС – равнобедренные с основаниями КМ и MС соответственно. Заметим, что Ð КAМ = Ð КAB + Ð BAМ = 60° + 30° = 90° , а Ð MDС = 30° . Следовательно, Ð КМА = 45° , Ð DМС = 75° . То есть, Ð КМС = Ð КМА +Ð АМD +Ð DМС = 45° + 60° + 75° = 180° , то есть, точки С, М и K лежат на одной прямой.

3.3. В трехзначном числе зачеркнули цифру в разряде сотен, затем полученное двухзначное число умножили на 7 и вновь получили исходное трехзначное число. Какое это число?

Ответ: 350.

Пусть – десятичная запись исходного числа, тогда . Так как , то, разделив обе части на 2, получим равенство: . Числа 50 и 3 взаимно просты, поэтому а делится на 3. С нуля трехзначное число начинаться не может; если а = 6 или а = 9, то число не будет двузначным, поэтому, а = 3; = 50.

Отметим, что возможны также «переборные» решения, основанные на том, что при умножении числа на 7 не изменилась последняя цифра, поэтому с = 0 или с = 5. Кроме того, из условия задачи следует, что а < 7.

4.1. Докажите, что число является квадратом натурального числа.

Пусть , тогда данное число равно: = = . Следовательно данное число равно квадрату натурального числа .

4.2. Треугольник, один из углов которого равен 40° , разрезали по его биссектрисам на шесть треугольников, среди которых есть прямоугольные. Какими могли быть остальные углы исходного треугольника?

Ответ: два угла по 70° или 40° и 100° .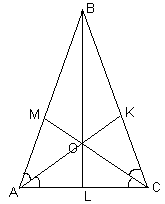

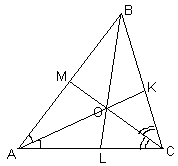
Пусть АВС – данный треугольник с углом В, равным 40° ; AK, BL и СM – его биссектрисы, пересекающиеся в точке О (см. рис. 5 а, б).

Докажем, что ни один из образовавшихся углов с вершиной О не может быть прямым. Действительно, если Ð AOC = 90° , то Ð OАC + Ð OCА = 90° , следовательно, Ð BАC + Ð BCА = 180° , что невозможно. Если же Ð LOC = 90° , то смежный с ним Ð BOC = 90° , и мы приходим к уже разобранному случаю.

Таким образом, прямыми могут быть только углы с вершинами в точках М, К и L. Возможны два случая: 1) прямым является угол, например, при вершине L (см. рис. 5а); 2) прямым является один из углов: либо при вершине K, либо при вершине М (см. рис. 5б).

В первом случае биссектриса BL является высотой треугольника, то есть, треугольник АВС – равнобедренный с основанием АС и его углы: 40° ; 70° ; 70° . Во втором случае треугольник АВС также равнобедренный, но с основанием АВ (либо с основанием ВС) и его углы: 40° ; 40° ; 100° .

Заметим, что так как треугольник АВС не равносторонний, то только одна из биссектрис данного треугольника может быть перпендикулярна стороне.

4.3. Буратино зарыл на Поле Чудес золотую монету. Из нее выросло дерево, а на нем – две монеты: серебряная и золотая. Серебряную монету Буратино спрятал в карман, а золотую зарыл, и опять выросло дерево ... . Каждый раз на дереве вырастали две монеты: либо две золотые, либо золотая и серебряная, либо две серебряные. Серебряные монеты Буратино складывал в карман, а золотые закапывал. Когда закапывать стало нечего, в кармане у Буратино было 2004 серебряные монеты. Сколько монет закопал Буратино?

Ответ: 2003.

Назовем монету, из которой что-то выросло – «родителем», а монету, которая выросла из какой-нибудь монеты – «ребенком». Заметим, что «детьми» являются все монеты, кроме первой, а каждая золотая монета (и только она) является «родителем». Поскольку у каждого «родителя» – два «ребенка», то «детей» – в два раза больше, чем «родителей».

Пусть x – количество золотых монет, а y – количество серебряных, тогда всего монет будет x + y, из которых «детьми» являются (x + y) – 1 монет, а «родителями» – x. Составляем уравнение: (x + y) – 1 = 2x Û x = y – 1, то есть, количество золотых монет меньше количества серебряных на 1, следовательно, Буратино закопал 2003 монеты.