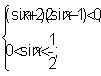 Û
Û
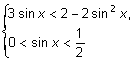 Û
Û
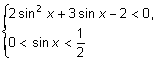 Û
Û
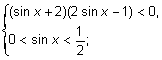 ;
; 10
класс.1.1.
(6 баллов) Найдите все целые решения неравенства: |x + 3y – 5,5| + |x – 3y| £Ответ
: (3; 1).Пусть (
x; y) – решение неравенства. Тогда из условия задачи следует, что |x – 3y| < 1. Так как x и y – целые числа, то x = 3y. Подставим этот результат в исходное неравенство, тогда: |6y – 5,5| £Проверка показывает, что (3; 1) является решением исходного неравенства.
Возможно также «лобовое решение», основанное на раскрытие модулей, но тогда придется рассмотреть четыре случая, поэтому такое решение является очень трудоемким.
1.2.
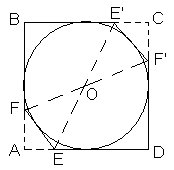
(6 баллов) Противоположные стороны шестиугольника попарно равны и параллельны, кроме того, в него можно вписать окружность. Обязательно ли этот шестиугольник – правильный?Ответ: нет, не обязательно.
Например, рассмотрим квадрат АВС
D и вписанную в него окружность. Проведем две касательные к окружности, симметричные относительно ее центра О (см. рис. 1). Тогда шестиугольник EFBE’F’D удовлетворяет условию задачи, но не является правильным, так как в нем есть прямые углы.Можно привести и более общий пример: достаточно рассмотреть окружность с центром О и построить описанную около нее ломаную
EFBE’, у которой не все звенья между собой равны, а точки Е и E’ симметричны относительно О. Искомый шестиугольник получится из этой ломанной симметрией относительно точки О и не будет правильным.1.3. (6
баллов) В некотором числе переставили цифры и получилось в три раза меньшее число. Докажите, что исходное число делилось на 27.Пусть А – исходное число, В – число, полученное после перестановки цифр. Тогда, по условию, А = 3В, то есть А кратно трем, следовательно сумма цифр числа А делится на 3. Поскольку число В записывается теми же цифрами, что и число А, то оно также кратно трем, следовательно, А делится на 9, тогда и В делится на 9. Таким образом, А = 3В делится на 27.
Числа, указанные в условии, существуют, например, А = 3105; В = 1035
.2.1. (7
баллов) Найдите все значения параметра а, для которых система уравнений имеет единственное решение.
имеет единственное решение.
Ответ
: а = 0.Заметим, что если (
m; n) – решение данной системы, то (n; m) – также решение этой системы. Следовательно, если данная система имеет единственное решение, то оно имеет вид (m; m). Получим: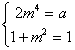 Û
Û
При а = 0 данная система действительно имеет единственное решение, так как
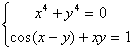 Û
x = y = 0.
Û
x = y = 0.
2.2. (7
баллов) В остроугольном треугольнике ABC проведены высоты AA1 и CC1. На высоте AA1 выбрана такая точка D, что A1D = C1D. Точка E – середина стороны AC. Докажите, что точки A, C1, D и E лежат на одной окружности.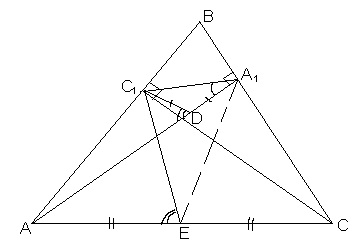
Из условия задачи следует, что точки
A, C1, A1 и С лежат на окружности с центром в точке E и радиусом EА. Поэтому, вписанный в нее угол C1A1A в два раза меньше центрального угла C1EA, опирающегося на ту же дугу. С другой стороны, треугольник C1DA1 – равнобедренный, следовательно его внешний угол C1DA в два раза больше угла C1A1A. Таким образом, Ð C1DA = Ð C1EA, поэтому точки A, C1, D и E лежат на одной окружности.2.3.
(7 баллов) Имеет ли уравнение 5x4 = 4y3 + 3 целочисленные решения?Ответ
: нет, не имеет.При целых значениях у правая часть уравнения при делении на 4 дает остаток 3. Левая часть уравнения при четных значениях х делится на 4, а при нечетных значениях х при делении на 4 дает остаток 1. Действительно, если х = 2k + 1, где k – целое число, то 5х4 = (4 + 1)(2k + 1)4 = (4 + 1)(4k2 + 4k + 1)2 = 4(4k2 + 4k + 1)2 + (4k2 + 4k)2 + 2(4k2 + 4k) + 1 = 4p + 1, где p – целое число.
Полученное противоречие показывает, что данное уравнение не имеет целочисленных решений.
3.1.
(7 баллов) Докажите, что еслиТак как
Пусть данная сумма
S = S1 + S2, где S1 = sinx + sin3x + ...; S2 = tg2x + tg4x + ... , то есть, S1 – сумма бесконечно убывающей геометрической прогрессии с первым членом sinx и знаменателем sin2x, а S2 – сумма бесконечно убывающей геометрической прогрессии с первым членом tg2x и знаменателем tg2x. Тогда S1 =Так как на
[0;Аналогично, на
[0;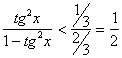 .
.
Таким образом, если
Справедливость использованных при решении неравенств
S1 <1) 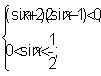 Û
Û
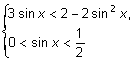 Û
Û
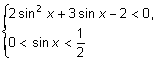 Û
Û
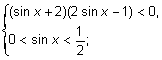 ;
;
2) 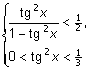 Û
Û
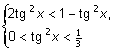 Û
Û
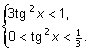
Отметим также, что существенным моментом решения является ссылка на то, что все члены данной бесконечной суммы положительны. В противном случае разбиение бесконечной суммы на несколько сумм может приводить к неожиданным результатам.
Например, рассмотрим бесконечную сумму: S = 1 – 1 + 1 – 1 + 1 – 1 + ... . Группируя слагаемые по два, начиная с первого: S = (1 – 1) + (1 – 1) + (1 – 1) + ..., получим, что S = 0. Группируя их по два, начиная со второго: S = 1 + (–1 + 1) + (–1 + 1) +..., получим, что S = 1. Переставив соседние слагаемые местами, и группируя их, начиная со второго: S = –1 + (1 – 1) + (1 – 1) + ..., получим, что S = –1. И наконец, можно записать данную сумму так:
S = 1 – (1 – 1 + 1 – 1 + ... ) и составить уравнение S = 1 – S, откуда S = 0,5.3.2. (7 баллов) Внутри треугольника выбраны две точки. Расстояния от одной из них до сторон треугольника равны 1, 3 и 15, а от другой (стороны рассматриваются в том же порядке) – 4, 5 и 11. Найдите радиус окружности, вписанной в данный треугольник.
Ответ: 7.
Первый способ
. Пусть a, b и c – длины сторон данного треугольника АВС, а S – его площадь. Проведем отрезки, соединяющие одну из данных точек М с вершинами треугольника (см. рис. 3а). Тогда: a + 3b + 15c = 2S. Аналогично, соединив другую данную точку с вершинами треугольника, получим, что 4a + 5b + 11c =2S.Умножим второе уравнение на 2 и вычтем первое. Получим: 7
a + 7b + 7c = 2S, откуда найдем радиус окружности, вписанной в треугольник: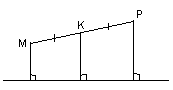
Второй способ
. Пусть М и K соответственно – точки, указанные в условии. Рассмотрим точку P, симметричную точке М относительно K. Воспользуемся тем, что если отрезок не пересекает прямую, то расстояние от его середины до этой прямой равно полусумме расстояний от его концов до этой прямой. Этот факт непосредственно следует из теоремы Фалеса и свойства средней линии трапеции (см. рис. 3б). Тогда расстояния от точки P до каждой из прямых, содержащих стороны треугольника, равно 7, то есть P равноудалена от этих прямых. При этом точка P лежит внутри данного треугольника (если бы отрезок МР пересекал какую-то из сторон треугольника, то расстояние от его середины K до прямой, содержащей эту сторону, было бы равно модулю полуразности расстояний от М и Р), поэтому, искомый радиус вписанной окружности равен 7.3.3.
(7 баллов) Пятизначное число назовем «неразложимым», если оно не раскладывается в произведение двух трехзначных чисел. Какое наибольшее количество таких чисел может идти подряд?Ответ
: 99.Рассмотрим все натуральные числа от А = 100·100 + 1 до В = 100·101 – 1. Ни одно из таких чисел нельзя разложить в произведение двух трехзначных, так как числа 100 и 101 – наименьшие трехзначные. Таким образом получим 99 «неразложимых» чисел, идущих подряд.
Большего количества «неразложимых» чисел, идущих подряд, быть не может, так как из любых ста идущих подряд пятизначных чисел одно будет делиться на 100, причем частное от деления пятизначного числа на 100 будет трехзначным.
4.1.
(8 баллов) Докажите, что для любых значений x выполняется неравенство:1)
При x = 0 данное неравенство, очевидно, выполняется.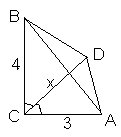
2) Заметим, что значение левой части неравенства при любом отрицательном значении
x больше, чем при противоположном положительном значении x, поэтому достаточно доказать, что неравенство выполняется при x > 0.Рассмотрим прямоугольный треугольник
ABC с прямым углом C и катетами AC = 3; BC = 4 (см. рис. 4). На биссектрисе угла С отметим точку D такую, что CD = x.Применяя теорему косинусов для треугольников
ADC и BDC, соответственно получим:Согласно неравенству треугольника
AD + BD ³ AB, откуда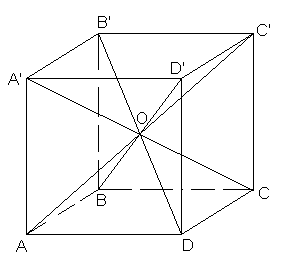
4.2. (8
баллов) Можно ли разрезать куб на три равные части, не являющиеся ни параллелепипедами, ни пирамидами?Ответ
: да, можно.Первый способ. Проведем отрезки, соединяющие центр О куба АВСDA’B’C’D’ с его вершинами (см. рис. 5). Проходящие через них плоскости разобьют куб на шесть равных четырехугольных пирамид, у которых основаниями являются грани куба, а вершиной – точка О. Объединив по две соседние пирамиды, например, OABCD и OAA’B’B; OA’B’C’D’ и OAA’D’D; OBB’C’C и OCC’D’D, получим три равные фигуры, не являющиеся ни параллелепипедами, ни пирамидами.
Второй способ (идея – школьников СУНЦа). Рассмотрим одну из диагоналей куба, например, B’D. Проведем три полуплоскости с границей B’D так, чтобы угол между каждыми двумя был равен 120° . Они разобьют куб на три равные части, так как одна из другой получается поворотом вокруг прямой B’D на 120° . Несложно выбрать полуплоскости таким образом, чтобы они не содержали ребра куба, тогда получившиеся части не окажутся пирамидами.
4.3.
(8 баллов) На шахматной доске стоят черная и белая шашки. За один ход разрешается сдвинуть одну из них на соседнюю (по стороне) клетку. Существует ли такая последовательность ходов, при которой каждое возможное расположение шашек встречается ровно один раз?Ответ: нет, не
существует.Заметим, что если в некоторый момент обе шашки находятся на клетках одного цвета, то после любого допустимого хода шашки окажутся на клетках разного цвета, и наоборот. Таким образом, позиции, в которых шашки стоят на клетках одного цвета, и позиции, в которых шашки стоят на клетках разного цвета, чередуются. Если требуемая последовательность ходов существует, то либо позиций обоих типов одинаковое количество, либо позиций одного типа на одну больше, чем позиций другого типа.
Подсчитаем сначала количество позиций, когда обе фишки стоят на клетках одного цвета. Белую фишку можно поставить на любую из 64 клеток, после чего черную можно поставить на любую свободную клетку того же цвета, которых – 31. Итого: 64´ 31 позиций. Теперь подсчитаем количество позиций другого типа. Белую фишку опять можно поставить на любую из 64 клеток, а черную – на любую из 32 клеток другого цвета. Итого
: 64´ 32 позиций. Так как 64´ 32 – 64´ 31 = 64 > 1, то требуемой последовательности ходов не существует.5.1.
(9 баллов) Существует ли многочлен P(x) такой, что P(1) = 1, P(2) = 2, P(3) = 3, P(4) = 4, P(5) = 5, а его значения при всех остальных натуральных x – иррациональны?Ответ
: да, существует.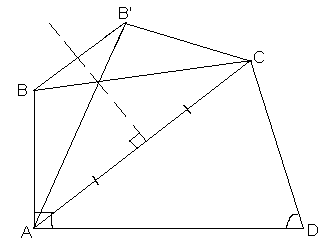
Например, если P(x) = x + ![]() (x – 1)(x – 2)(x – 3)(x – 4)(x – 5), то такой многочлен, очевидно, принимает значения, указанные в условии. При x = n, где nÎ
N и n > 5, его значения имеют вид: P(n) = n + m
(x – 1)(x – 2)(x – 3)(x – 4)(x – 5), то такой многочлен, очевидно, принимает значения, указанные в условии. При x = n, где nÎ
N и n > 5, его значения имеют вид: P(n) = n + m![]() , где m – также натуральное число, поэтому P(n) – иррационально.
, где m – также натуральное число, поэтому P(n) – иррационально.
5.2. (9
баллов) В выпуклом четырехугольнике АВСD: BC = 4, Ð АDС = 60° , Ð BАD = 90° .Ответ
:Пусть АВС
D – данный четырехугольник (см. рис. 6а). Отразим вершину B симметрично относительно серединного перпендикуляра к отрезку AC и получим точку B’. Тогда B’A = BC, CB’ = AB и SAB’C = SABC.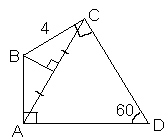
Следовательно,
SAB’CD = SABCD =Так как Ð
B’AD = Ð BAD = 90° , то лучи AB’ и AB совпадают, следовательно, симметричные точки В и B’ также совпадают (см. рис. 6б). Тогда ВА = ВС, Ð BAC = Ð BCA и Ð DAC = Ð DCA = 60° , то есть D ADC – равносторонний. Следовательно, Ð BAC = Ð BCA = 30° , значит, СD = CA =5.3. (9
баллов) Каких треугольников с целыми сторонами больше: с периметром 2005 или с периметром 2008?Ответ
: одинаково.1) Каждому треугольнику со сторонами a £ b £ c и периметром 2005 поставим в соответствие треугольник со сторонами a + 1 £ b + 1 £ с + 1 и периметром 2008. Такой треугольник существует, так как (а + 1) + (b + 1) > (a + b) + 1 > c + 1.
2) Пусть есть треугольник со сторонами
x £ y £ z и периметром 2008, тогда рассмотрим отрезки с длинами x – 1; y – 1; z – 1. Очевидно, что эти числа – натуральные (если, например, x – 1 = 0 Û x = 1, то y + z = 2007 и треугольника со сторонами 1, y и z, где y и z – целые, не существует).Кроме того,
(x – 1) + (y – 1) = (x + y) – 2 > z – 2. Так как эти числа – натуральные, то отсюда следует, что (x – 1) + (y – 1) ³ z – 1. Поэтому, рассматриваемые отрезки не образуют треугольника только в случае, когда (x – 1) + (y – 1) = (z – 1) Û x + y = z + 1. Тогда P = x + y + z = 2z + 1 – нечетное число, поэтому не может быть равно 2008.Следовательно,
(x – 1) + (y – 1) > z – 1, то есть каждому треугольнику со сторонами x £ y £ z и периметром 2008 поставлен в соответствие треугольник со сторонами x – 1 £ y – 1 £ z – 1 и периметром 2005.Таким образом, указанное соответствие между множествами треугольников взаимно однозначное, и треугольников с целыми сторонами и периметром 2005 столько же, сколько с периметром 2008.