7 класс.

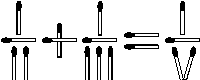
1.1. (6 баллов) Из спичек сложено неверное равенство: Переложите одну спичку так, чтобы равенство стало верным.

Ответ:

 

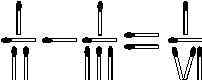
1.2. (6 баллов) Вася вырезал из картона треугольник, разрезал его на два треугольника и послал обе части Пете, который также сложил из них треугольник. Верно ли, что Петин треугольник обязательно равен Васиному?

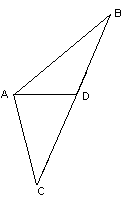
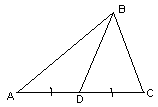
Ответ: Нет, неверно.

Например, если Вася разрезал остроугольный треугольник АВС по медиане BD (см. рис. слева), а Петя сложил треугольник так, как это показано на рис. справа.

1.3. (6 баллов) Средний рост восьми баскетболистов равен 195 см. Какое наибольшее количество из этих игроков может быть ниже, чем 191 см?

Ответ: семь.

Например, если один баскетболист имеет рост 230 см, то рост остальных может быть 190 см, так как (230 + 190× 7) : 8 = 195.

2.1. (7 баллов) Температуру можно измерять в градусах Цельсия и Фаренгейта. Известно, что вода замерзает при 0° С, что соответствует 32° F, а кипит при 100° С или при 212° F. Сейчас на улице 5 градусов мороза по Цельсию. Какова температура по Фаренгейту?

Ответ: 23° F.

Из условия следует, что 100° С = 180° F, то есть, 1° С = 1,8° F. Поэтому, 5 градусам мороза по Цельсию соответствуют: 32° F – 5× 1,8° F = 23° F.

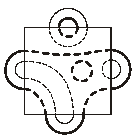
2.2. (7 баллов) На столе лежат шесть непересекающихся контуров из проволоки, частично накрытые листом бумаги (см. рис.слева). Известно, что три контура сделаны из медной проволоки (она потолще), а три – из тонкой алюминиевой, причем один из контуров закрыт полностью, а пять других частично видны. Какой контур закрыт полностью, алюминиевый или медный? Свой ответ достаточно проиллюстрировать рисунком, показывающим расположение всех шести контуров.

Ответ: полностью закрыт медный контур.

Возможное расположение контуров – см. рис. справа.

2.3. (7 баллов) Найдите наименьшее составное число, которое не делится ни на одно из натуральных чисел от двух до десяти.

Ответ: 121.

Любое составное число является произведением не менее чем двух простых множителей. Из условия задачи следует, что каждый из этих множителей не может быть меньше, чем 11. Значит, искомое число не меньше, чем 112 = 121, а это число удовлетворяет условию.

3.1. (7 баллов) Все акции компаний «Карабас» и «Барабас» вместе стоят 90 золотых монет. У Буратино есть 25% акций компании «Карабас» и 75% акций компании «Барабас» общей стоимостью 30 золотых монет. Найдите стоимость всех акций каждой компании.

Ответ: все акции компании «Карабас» стоит 75 золотых монет, а компании «Барабас» – 15 золотых монет.

Из условия следует, что 100% акций компании «Карабас» и 300% акций компании «Барабас» стоят 120 монет. Значит, 200% акций компании «Барабас» стоят 120 – 90 = 30 золотых монет. Тогда все акции компании «Барабас» стоит 15 монет, а все акции компании «Карабас»: 90 – 15 = 75 (монет).

По условию задачи можно составить систему уравнений , где x и y – искомые стоимости акций. Решение, приведенное выше, соответствует решению этой системы способом сложения.

3.2. (7 баллов) На плоскости расположены пять точек А, В, С, D и Е так, что АС = 5 см, AE = 4 см; ВС = 14 см, BD = 2 см, DE = 3 см. Найдите расстояние между серединами отрезков AB и CD.

Ответ: 3,5 см.

Так как BD + DE + EA + AC = BC, то точки A, D и E лежат на отрезке ВС так, как это показано на рис. Тогда AB = 9 см; CD = 12 см.

Искомое расстояние можно, например, вычислить так: середина отрезка АВ удалена от точки В на половину длины АВ, то есть, на 4,5 см. Середина отрезка CD удалена от точки C на половину длины CD, то есть, на 6 см. Следовательно, расстояние между серединами отрезков AB и CD равно 14 – 4,5 – 6 = 3,5.

Для вычисления расстояния можно также рассмотреть координатный луч ВС и воспользоваться координатными формулами середины отрезка и расстояния между точками координатной прямой.

3.3. (7 баллов) В ряд выложили несколько апельсинов, мандаринов, яблок и груш. Известно, что рядом с фруктом каждого вида можно найти фрукт любого другого вида. Какое наименьшее количество фруктов могло быть выложено?

Ответ: 8.

Рассмотрим какой-то фрукт в ряду, например апельсин. У него не более двух соседей. Следовательно, чтобы апельсины встречались в паре с тремя другими видами фруктов, необходимо не менее двух апельсинов. Аналогичные рассуждения показывают, что выложено не менее двух мандаринов, не менее двух яблок и не менее двух груш. Значит, всего фруктов должно быть не менее восьми.

Этого количества фруктов достаточно для выполнения условия задачи, например: апельсин, мандарин, яблоко, груша, апельсин, яблоко, мандарин, груша.

4.1. (8 баллов) Вася задумал число и прибавил к этому числу его сумму цифр. Петя также задумал число и тоже прибавил к нему его сумму цифр. В результате сложения у Васи и Пети получились одинаковые числа. Верно ли, что они задумывали одинаковые числа?

Ответ: нет, неверно.

Например, если Вася задумал число 91, а Петя – число 100, то оба получили сумму 101.

Отметим, что среди двузначных чисел нельзя найти два различных числа, у которых равны сумма самого числа и его суммы цифр. Действительно, пусть два таких числа = 10а + b и = 10c + d существуют, тогда 11а + 2b = 11c + 2d Û 11(a – c) = 2(d – b). Если b = d, то а = с, тогда = . Если b ¹ d, то d – b делится на 11, что невозможно, так как d и b – цифры.

4.2. (8 баллов) Квадрат со стороной 1 разрезали на прямоугольники периметра 2. Сколько прямоугольников могло получиться? (Укажите все возможные значения и обоснуйте.)

Ответ: могло получиться любое количество прямоугольников, большее трех.

1) Покажем, что невозможно разрезать данный квадрат меньше, чем на четыре прямоугольника с периметром 2. Действительно, каждый из четырех углов квадрата является одновременно и углом одного из прямоугольников. Если нам удалось разрезать квадрат на 1, 2 или 3 прямоугольника с периметром 2, то хотя бы один из них занимает 2 угла. То есть, у такого прямоугольника две стороны равны стороне квадрата, следовательно, его периметр больше двух.

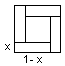
2) Разрезание квадрата со стороной 1 на четыре квадрата со стороной (см. рис. справа) удовлетворяет условию задачи.

3) Разрежем квадрат на 4 одинаковых прямоугольника и квадрат так, как это показано на рис. слева. Пусть одна из сторон прямоугольника равна x, тогда другая сторона имеет длину 1 – x, поэтому периметр каждого из этих прямоугольников равен 2 независимо от значения x. Сторона «центрального» квадрата равна 1 – 2x, то есть, его периметр равен 4 – 8x. Следовательно, это разбиение удовлетворяет условию задачи при x = .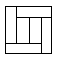

4) Для того, чтобы разрезать данный квадрат на 6 прямоугольников периметра 2 достаточно разбить «центральный» квадрат на два равных прямоугольника (см. рис. справа). В этом случае периметр каждого из них будет равен , то есть, x = .

Аналогично, изменяя значение x, можно разбивать центральный квадрат на любое количество равных прямоугольников, увеличивая тем самым количество прямоугольников в разрезании данного квадрата.

В общем виде: для того, чтобы разрезать данный квадрат на n прямоугольников с периметром 2 достаточно разбить «центральный» квадрат на n – 4 одинаковых прямоугольника. Периметр каждого из них равен . По условию, это выражение должно быть равно 2, то есть, , следовательно, . Отметим, что эта формула применима и для «вырожденного» случая n = 4, рассмотренного в пункте 1).

4.3. (8 баллов) В вершинах треугольника записаны числа 1, 2 и 3. Затем каждое из чисел одновременно заменили на сумму двух соседних. Эту операцию проделали еще некоторое количество раз. Могла ли сумма получившихся в итоге трех чисел оказаться равной 3000000?

Ответ: нет, не могла.

Пусть в какой-то момент в вершинах записаны числа а, b и с. Тогда после указанной операции вместо них будут записаны числа b + c, c + a и a + b. Так как (b + c) + (c + a) + (a + b) = 2(a + b + c), то после каждой операции сумма трёх записанных чисел удваивается. Сумма исходных чисел не делится на 5, поэтому и сумма чисел, полученных после любого количества операций, на 5 делиться не может.