1.1. Найдите x + y, если x³ + y³ = 9, а x²y + xy² = 6.

Ответ: 3.

Первый способ. Так как (x + y)³ = x³ + 3x²y + 3xy² + y³ = (x³ + y³) + 3(x²y + xy²) = 9 + 18 = 27, то x + y = 3.

Второй способ. Так как x³ + y³ = (x + y)(x² – xy + y²) = (x + y)((x + y)² – 3xy) = (x + y)³ – 3xy(x + y), а 3xy(x + y) = 3(x²y + xy²) = 18, то 9 = (x + y)³ – 18, то есть, x + y = 3.

1.2. В треугольнике АВС медиана ВЕ перпендикулярна биссектрисе AD. Найдите длину АВ, если АС = 12.

Ответ: 6.

Пусть F – точка пересечения AD и ВЕ (см. рис. 1). В треугольнике АВЕ биссектриса AF является высотой, поэтому этот треугольник – равнобедренный. Следовательно, АВ = АЕ = АС = 6.

1.3. У Васи есть карточки с цифрами 1, 2, 3 и 4 – по две с каждой цифрой. Он хочет сложить из них число так, чтобы между двумя единицами была одна цифра, между двойками – две цифры, между тройками – три, а между четверками – четыре. Укажите какое-нибудь число, которое может получить Вася.

Ответ: 41312432 или 23421314.

2.1. Известно, что а + b + c = 7, а . Найдите сумму: .

Ответ: 1,9.

Перемножим почленно данные верные равенства: Û Û .

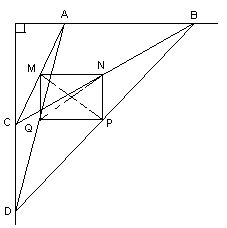
2.2. Отрезки АВ и CD лежат на перпендикулярных прямых (см. рис.). Точки М, Р, N и Q – середины отрезков АС, BD, ВС и AD соответственно. Найдите QN, если MP = 4 см.

Ответ: 4 см.

Рассмотрим четырехугольник MNPQ (см. рис. 2). Из условия задачи следует, что MN – средняя линия треугольника АСВ, поэтому MN || AB и MN = 0,5AB. Аналогично, так как PQ – средняя линия треугольника АDВ, то PQ || AB и PQ = 0,5AB. Таким образом, MN || PQ и MN = PQ, то есть, MNPQ – параллелограмм.

Кроме того, так как MQ – средняя линия треугольника CАD, то MQ || CD. Из того, что АВ ^ CD, MN || AB и MQ || CD, следует, что MN ^ MQ, то есть, MNPQ – прямоугольник. По свойству диагоналей прямоугольника: QN = MP = 4.

2.3. В шахматном турнире каждый участник встретился с каждым ровно один раз (победа – 1 очко, поражение – 0, ничья – пол-очка). Все шахматисты набрали одинаковое количество очков. Если удалить любого участника и аннулировать результаты встреч с ним, то количество очков у всех остальных участников по-прежнему будет одинаковым. Верно ли, что все партии этого турнира закончились вничью?

Ответ: Да, верно.

Так как после удаления одного участника оставшиеся шахматисты по-прежнему имеют одинаковый результат, то с этим участником все сыграли одинаково. Если бы этот шахматист выиграл все партии или проиграл все партии, то количество набранных им очков не могло бы быть таким же, что и у остальных участников, как это сказано в условии задачи. Следовательно, удаленный участник закончил все свои партии вничью.

Поскольку аналогичное рассуждение можно провести для каждого из шахматистов, то все партии турнира закончились вничью.

3.1. Дано уравнение c переменной x: (a² – 1)(b – 1)x = (a – 1)(b² – 1). При каких значениях а найдется значение b такое, что данное уравнение не имеет корней?

Ответ: при а = –1.

Данное уравнение имеет вид сx = d, где с и d – некоторые числа, то есть является линейным. Такое уравнение не имеет корней тогда и только тогда, когда с = 0, d ¹ 0.

Следовательно, 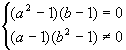Û Û .

Таким образом, при a = –1 найдется значение b (любое, кроме чисел 1 и –1), удовлетворяющее условию.

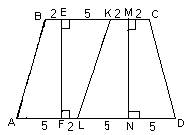
3.2. Дана равнобокая трапеция с основаниями 11 и 17. Покажите, как ее можно разрезать на четыре равные трапеции.

Ответ: см. рис. 3.

Пусть ABCD – данная равнобокая трапеция, у которой AD = 17, BC = 11 (см. рис. 3). Выберем на ее основаниях BC и AD соответственно точки K и L так, что BK = AL = 7. Тогда ABKL – параллелограмм, а DCKL – равнобокая трапеция с основаниями 4 и 10. Отрезок EF проходит перпендикулярно BK и AL через центр симметрии параллелограмма, а MN – ось симметрии трапеции DCKL, поэтому в трапециях АВЕF, KLFE, LKMN и DCMN равны соответствующие стороны и равны соответствующие углы.

3.3. В вершинах куба расставлены числа от 1 до 8. На каждой грани записана сумма чисел, расставленных в ее вершинах. Может ли оказаться так, что на гранях записано шесть последовательных натуральных чисел?

Ответ: нет, не может.

Пусть на гранях записано шесть последовательных натуральных чисел, n – наименьшее из них, а S – их сумма. Тогда S = n + (n + 1) + ... + (n + 5) = 6n + 15. Так как каждая вершина принадлежит трем граням куба, то каждое число от 1 до 8 входит в три суммы, записанные на гранях. Поэтому, S = (1 + 2 + … + 8)× 3 = 108. Уравнение 6n + 15 = 108 не имеет натуральных решений, так как в его левой части – нечетное число, а в правой части – четное.

Ответ: 9 человек.

Первый способ. Пусть в третьем ряду сидит x человек. Так как средний возраст равен сумме возрастов, деленной на количество человек, то после пересаживания суммарный возраст детей на первом ряду увеличился на 12 недель, на втором ряду – увеличился на 24 недели, а на третьем ряду – уменьшился на 4x недель. Поскольку сумма возрастов всех учеников изменится не могла, то 4x = 12 + 24, то есть, x = 9.

Второй способ. Пусть до пересаживания учеников средний возраст сидящих на первом, втором и третьем ряду составлял а, b и c недель соответственно. Обозначим также: количество человек, сидящих в третьем ряду – x, возраст Вовочки – V недель, возраст Ванечки – W недель, возраст Машеньки – М недель.

Исходя из условия задачи, составим три уравнения: 1) ; 2) ; 3) . Упростив эти уравнения и объединив их в систему, получим: 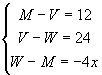. Сложив все уравнения почленно, получим, что 12 + 24 – 4x = 0, то есть, x = 9.

4.2. Угол ВАС треугольника АВС равен 120° . На биссектрисе этого угла взята точка D так, что АD = AB + AC. Найдите углы треугольника BDC.

Ответ: три угла по 60° .

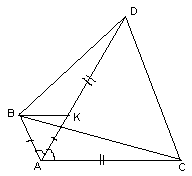
Первый способ. Отложим на луче AD отрезок AK, равный АВ (см. рис. 4а). Тогда D BAK – равнобедренный с углом 60° , то есть, D BAK – равносторонний. Следовательно, BK = BA, DK = AD – AK = AD – AB = CA и Ð BKD = 180° – Ð BKA = 120° = Ð BAC. Тогда D BKD = D BAС (по двум сторонам и углу между ними), поэтому BD = BC и Ð DBC = Ð DBK + Ð CBK = Ð CBA + Ð CBK = 60° . Таким образом, D BDC – равнобедренный с углом 60° , то есть, D BDC – равносторонний.

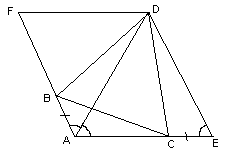
Второй способ. Проведем прямые DE и DF, соответственно параллельные прямым АВ и АС (см. рис. 4б), тогда AEDF – параллелограмм, в котором диагональ AD является биссектрисой угла, то есть, AEDF – ромб. Из условия задачи следует, что Ð DAF = Ð DAE = Ð DEA = 60° , то есть, сторона ромба равна его диагонали, в частности, AD = AE = ED. Следовательно, ЕC = AE – AC = AD – AC = AB. Тогда D ABD = D EСD (по двум сторонам и углу между ними), поэтому, BD = CD. Кроме того, Ð BDC = Ð BDA + Ð ADC = Ð EDC + Ð ADC = 60° . Таким образом, D BDC – равнобедренный с углом 60° , то есть, D BDC – равносторонний.

4.3. В некоторых клетках таблицы 100´ 100 стоят крестики. Каждый крестик является единственным либо в строке, либо в столбце. Какое наибольшее количество крестиков может стоять в таблице?

Ответ: 198.

Докажем, что в таблице не может быть больше, чем 198 крестиков. Действительно, количество крестиков, единственных в строке, не превышает количества строк, то есть, их не больше ста. Если их – ровно 100, то в каждой строке такой крестик есть, и тогда ни в какую из строк нельзя поставить еще крестик, поэтому, других крестиков в таблице быть не может. Аналогичное рассуждение можно провести, если имеется 100 крестиков, единственных в столбце. Если же и тех и других имеется не более чем по 99, то всего крестиков в таблице не больше, чем 99× 2 = 198.