1.1. (6 баллов) Известно, что уравнение ax⁵ + bx⁴ + c = 0 имеет ровно три действительных корня. Сколько корней может иметь уравнение cx⁵ + bx + a = 0?

Заметим, что среди корней уравнения ax⁵ + bx⁴ + c = 0 нет нуля, так как в этом случае с = 0, и уравнение примет вид x⁴(ax + b) = 0. Такое уравнение имеет либо бесконечно много действительных корней (при а = b = 0), либо не более двух.

Пусть t № 0 – корень исходного уравнения, тогда – корень уравнения cx⁵ + bx + a = 0. Действительно, Ы . Это означает, что количество действительных корней второго уравнения не меньше количества действительных корней первого уравнения.

1.2. (6 баллов) Существует ли замкнутая шестизвенная не плоская ломаная такая, что длины всех ее звеньев равны и углы между соседними звеньями равны?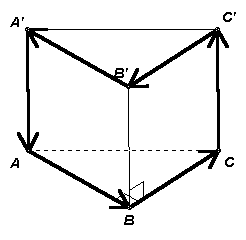

Ответ: да, существует.

Например, рассмотрим прямую треугольную призму ABCA’B’C’, в основании которой лежит равнобедренный прямоугольный треугольник, а боковое ребро равно катету этого треугольника (см. рис. 1а).

Тогда замкнутая ломаная ABCC’B’A’A имеет звенья одинаковой длины, а угол между любыми соседними звеньями – прямой.

Рассмотренная призма является «половиной» куба, поэтому аналогичный пример искомой ломаной может быть приведен на кубе.

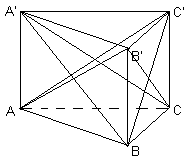
Можно также рассмотреть правильную треугольную призму ABCA’B’C’, у которой боковое ребро равно ребру основания (см. рис. 1б).

Тогда в качестве искомой ломаной можно взять, например, ломаную AB’CA’BC’A. Ее звеньями являются диагонали равных квадратов, а равенство углов между соседними звеньями следует из равенства треугольников AB’C, B’CA’, CA’B, A’BC’, BC’A и C’AB’ (по трем сторонам).

Существуют и другие примеры.

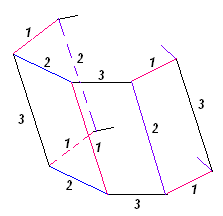
1.3. (6 баллов) Можно ли раскрасить в три цвета все ребра 99-угольной призмы так, что в каждой вершине сходятся все три цвета и у каждой грани (в том числе, у оснований) есть ребра всех трех цветов?

2.1. (7 баллов) Решите систему уравнений: .

Ответ: a = b = c = d = 0.

Сложив почленно данные уравнения, получим следствие из системы: 8a² + 9b² + 7c² + 4d² = 16ab + 8cd Ы (8a² – 16ab + 8b²) + (4c² – 8cd + 4d²) + b² + 3c² = 0 Ы 8(a – b)² + 4(c – d)² + b² + 3c² = 0 Ы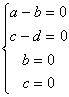 Ы a = b = c = d = 0. Полученная четверка чисел удовлетворяет исходной системе уравнений.

2.2. (7 баллов) В параллелограмме АВСD точки Е и F – середины сторон ВС и CD соответственно. Могут ли лучи АЕ и AF делить угол ВАD на три равные части?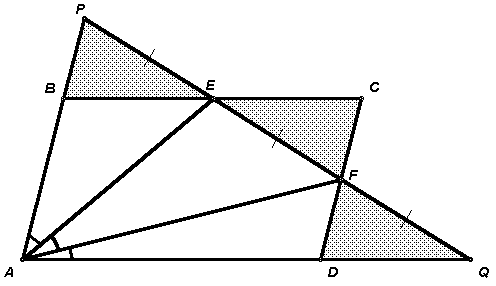

Ответ: нет, не могут.

Первый способ. Пусть прямая EF пересекает прямые АВ и CD в точках Р и Q соответственно (см. рис. 3а). Так как BE = EC (по условию), Р PBE = Р ECF (АВ || CD) и Р BEP = Р CEF, то равны треугольники BEP и CEF. Аналогично доказывается равенство треугольников DFQ и CFE. Следовательно, РЕ = EF = FQ.

Предположим, что равны углы ВАЕ, ЕАF и FAD. Тогда, из доказанного равенства получим, что АЕ – биссектриса и медиана треугольника PAF, а AF – биссектриса и медиана треугольника EAQ, то есть каждый из этих отрезков является также и высотой треугольника. Таким образом, из точки А проведены два различных перпендикуляра к прямой EF, что невозможно.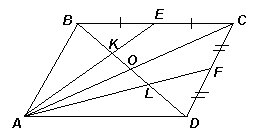

Второй способ. Пусть отрезки АЕ и АF пересекают диагональ BD данного параллелограмма в точках K и L соответственно (см. рис. 3б). Тогда BK = KL = LD. Это равенство можно доказать многими способами.

Например, пусть О – точка пересечения диагоналей параллелограмма, тогда с учетом равенства АО = ОС получим, что K – точка пересечения медиан треугольника АВС, поэтому BK = 2OK. Аналогично, L – точка пересечения медиан треугольника АDС, поэтому DL = 2OL. Учитывая, что ВО = OD, получим требуемое равенство.

Дальнейшие рассуждения аналогичны приведенным выше. Получим, что из точки А проведены два различных перпендикуляра к прямой BD, что невозможно.

В заключение заметим, что поскольку середины отрезков и прямые, параллельные данным, строятся циркулем и линейкой, а задача о трисекции угла (деление угла на три равные части с помощью циркуля и линейки) в общем случае неразрешима, то сразу возникает мысль, что описанная в условии конструкция невозможна. Тем не менее, это непосредственно не следует из неразрешимости задачи о трисекции угла, так как некоторые углы трисекцию допускают. Известна, например, следующая теорема: угол (nО N) можно циркулем и линейкой разделить на три равные части тогда и только тогда, когда n не делится нацело на 3. В частности, отсюда следует, что угол величиной 45° можно разделить на три равные части, а угол величиной 60° – нельзя.

2.3. (7 баллов) Натуральное число называется упрощенным, если оно является произведением ровно двух простых чисел (не обязательно различных). Какое наибольшее количество последовательных натуральных чисел может оказаться упрощенными?

Заметим, что больше трех последовательных упрощенных чисел быть не может. Действительно, среди четырех последовательных натуральных чисел ровно одно кратно четырем. Среди чисел, делящихся на 4, упрощенным является только само число 4 = 2Ч 2, но соседние с ним числа 3 и 5 упрощенными не являются.

Наименьшая тройка последовательных упрощенных чисел: 33 = 3Ч 11, 34 = 2Ч 17 и 35 = 5Ч 7. Для двузначных чисел есть еще два примера: 85 = 5Ч 17, 86 = 2Ч 43 и 87 = 3Ч 29; 93 = 3Ч 31, 94 = 2Ч 47 и 95 = 5Ч 19.

3.1. (8 баллов) Докажите неравенство: .

Первый способ. Заметим, что выполняются следующие числовые неравенства: ; ; ...; ; . Кроме того, для любых натуральных k выполняется равенство . Таким образом, < = = = , что и требовалось доказать.

Второй способ. Докажем, что для любого натурального n і 2 справедливо неравенство: . Воспользуемся методом математической индукции.

1) При n = 2 получим верное неравенство .

2) Предположим, что доказываемое неравенство верно при n = k, то есть . Докажем, что это неравенство будет верным и при n = k + 1. Действительно, , так как < = .

Следовательно, рассматриваемое неравенство выполняется для всех натуральных n і 2. Исходное неравенство получается из доказанного при n = 100.

3.2. (8 баллов) На отрезке АВ построена полуокружность, как на диаметре. На этой полуокружности выбраны произвольным образом точки P и Q. Точка С – пересечение прямых AP и BQ, а точка Х – пересечение касательных к полуокружности в точках Р и Q. Докажите, что прямые СХ и АВ перпендикулярны.

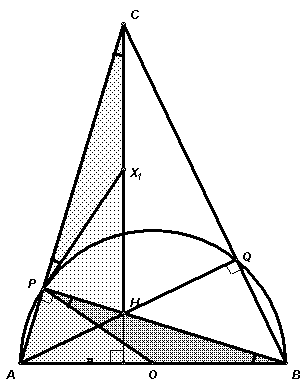
Пусть О – центр полуокружности. Для определенности, рассмотрим случай, когда H – точка пересечения прямых AQ и BP, расположена внутри полуокружности (см. рис. 4 а, б; для случая расположения точки Н вне полуокружности доказательство аналогично).

Так как Р АРВ = Р BQA = 90° , то AQ и BP являются высотами треугольника АВС. Так как высоты треугольника пересекаются в одной точке, то СH^ АВ.

Таким образом, для решения задачи достаточно доказать, что точка Х лежит на прямой СН. Рассмотрим точку Х₁ – середину отрезка СН и докажем, что она совпадает с точкой X.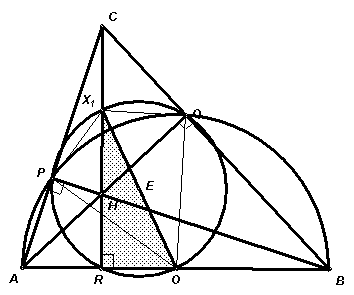

Первый способ. Так как PХ₁ – медиана прямоугольного треугольника CPH, проведенная к его гипотенузе (см. рис. 4а), то Р Х₁РВ = 90° – Р Х₁РС = 90° – Р Х₁СP = Р PAB. При этом, Р PAB – вписанный и опирается на дугу ВР. Следовательно, Х₁Р – касательная к данной полуокружности. Аналогично доказывается, что Х₁Q – также касательная к полуокружности.

Второй способ. Воспользуемся следующей классической теоремой: в любом треугольнике середины его сторон, основания высот и середины отрезков, соединяющих ортоцентр с вершинами, лежат на одной окружности, которую обычно называют окружностью девяти точек.

В нашем случае окружность девяти точек треугольника АВС будет проходить, в частности, через точки P, Q, Х₁, O и R – основание высоты, проведенной к стороне АВ (см. рис. 4б).

Так как Р Х₁RO = 90° , то Х₁O – диаметр этой окружности, поэтому Р Х₁РO = Р Х₁QO = 90° . Это и означает, что Х₁Р и Х₁Q – касательные к данной полуокружности.

3.3. (8 баллов) Таблица 5ґ 5 заполнена числами 1, 2, …, 25, причем любые два последовательных числа записаны в соседних (имеющих общую сторону) клетках. Какое наибольшее количество простых чисел может оказаться в одном столбце?

Ответ: 4.

Докажем, что в любых двух соседних клетках стоят числа разной четности. Пусть в некоторую клетку таблицы уже поставлено число N, тогда в двух соседних с ним клетках могут стоять только числа N – 1 и N + 1. Чтобы поставить числа в другую клетку, соседнюю с N, необходимо пройти «по цепочке», сделав нечетное число «шагов», каждый из которых меняет четность числа.

4.1. (9 баллов) Существует ли треугольник, в котором синус одного угла равен косинусу другого и равен тангенсу третьего?

Пусть a , b и g – углы треугольника, тогда по условию: .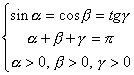

Так как sina > 0 при 0 < a < p , то cosb > 0 и tgg > 0, то есть углы b и g – острые.

1) Если , то из равенства sina = cosb следует, что . Тогда и tgg не существует, то есть этот случай невозможен.

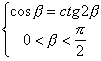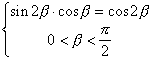2) Если , то sina = cosb Ы sin(p – a ) = sin( – b ), где углы p – a и – b не тупые. Следовательно, полученное равенство равносильно тому, что p – a = – b Ы a = + b . В этом случае tgg = tg(p – (a + b )) = tg( – 2b ) = ctg2b , то есть исходная система уравнений имеет решения тогда, и только тогда, когда имеет решения система Ы 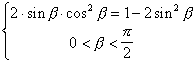Ы Ы 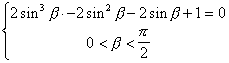. Пусть sinb = t, получим уравнение 2t³ – 2t² – 2t + 1 = 0.

Рассмотрим f(t) = 2t³ – 2t² – 2t + 1, тогда f(0) = 1 > 0; f(1) = –1 < 0, поэтому такое уравнение имеет хотя бы один корень на (0; 1). Это означает, что существует b , удовлетворяющее полученной системе, значит существует и треугольник, удовлетворяющий условию задачи.

Получив, что a = + b , можно рассуждать и по другому. Пусть угол b близок к нулю, тогда угол a немного больше , а угол g немного меньше . В этом случае sina и cosb близки к 1, а tgg очень велик, то есть sina = cosb < tgg .

4.2. (9 баллов) Во вписанном четырехугольнике длины двух противолежащих сторон равны а и b, острый угол между диагоналями равен j . Найдите все возможные значения радиуса окружности.

Ответ: .

Пусть в данном четырехугольнике ABCD: AD = a; BC = b; E – точка пересечения диагоналей. Вначале рассмотрим случай, когда Р CED = j (см. рис. 5).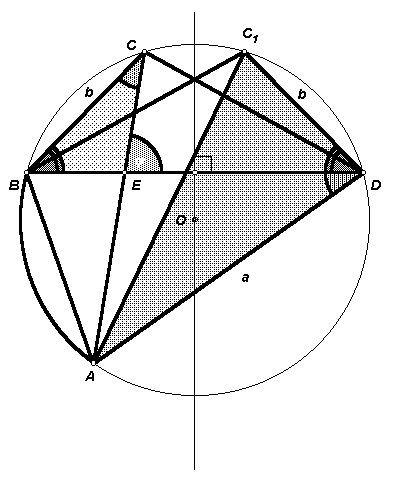

Рассмотрим симметрию, ось которой – серединный перпендикуляр к диагонали BD. При такой симметрии точки B и D переходят друг в друга, а окружность, описанная около ABCD, – в себя, так как центр О этой окружности лежит на оси. Поэтому образом точки С, лежащей на окружности, является точка С₁, также лежащая на окружности.

Симметрия сохраняет расстояния и величины углов, следовательно, DC₁ = BC = b и Р С₁DB = Р СBD. Кроме того, равны вписанные углы BDA и ВСА. Следовательно, Р С₁DA = Р С₁DB + Р BDA = Р СBD + Р ВСА = Р CED = j , так как Р CED – внешний угол треугольника ВЕС.

Рассмотрим треугольник ADC₁: по теореме косинусов = . Тогда по следствию из теоремы синусов = , где R – искомый радиус окружности.

Если данный угол j – смежный с углом СЕD, то в полученном выражении j заменяется на угол 180° – j .

4.3. (9 баллов) Может ли функция, непрерывная на множестве действительных чисел, принимать во всех рациональных точках иррациональные значения, а во всех иррациональных точках – рациональные?

Предположим, что существует функция f(x), удовлетворяющая условию задачи. Рассмотрим функцию g(x) = f(x) – x и докажем, что она принимает только иррациональные значения. Действительно, пусть g(a) рационально при некотором a. Если a – рационально, то f(a) = g(a) + a также рационально, что противоречит условию. Если a – иррационально, то по условию f(a) – рационально, тогда a = f(a) – g(a) должно быть рационально – противоречие.

Так как между любыми двумя иррациональными числами имеются рациональные, а функция g(x) – непрерывна (разность непрерывных функций), то она тождественно равна некоторой иррациональной константе c. Тогда f(c) = g(c) + c = 2c, но число 2c иррациональное, что противоречит условию задачи. Поэтому функции f(x), удовлетворяющей условию задачи, не существует.

5.1. (7 баллов) Найдите наибольшее и наименьшее значение выражения x² + xy + y², если 1 Ј x² + y² Ј 2.

Первый способ. 1) Воспользовавшись очевидным неравенством , получим, что . Равенство достигается, например, при x = y = 1.

2) Воспользовавшись очевидным неравенством , получим, что . Равенство достигается, например, при ; .

Второй способ. Из условия задачи следует, что существуют такие аО [1; ] и a О (–p ; p ], что x = aЧ cosa ; y = aЧ sina . Тогда x² + xy + y² = a² + a²Ч sina cosa = a²(1 + 0,5sin2a ). Так как –1 Ј sin2a Ј 1, то наибольшее значение полученного выражения достигается при а = , a = и равно 3, а наименьшее значение достигается при а = 1, a = – и равно 0,5.

5.2. (7 баллов) Во вписанном четырехугольнике АВСD точка М лежит на стороне AD, причем BM || CD и CM || BA. Найдите ВС, если АМ = а; DM = b.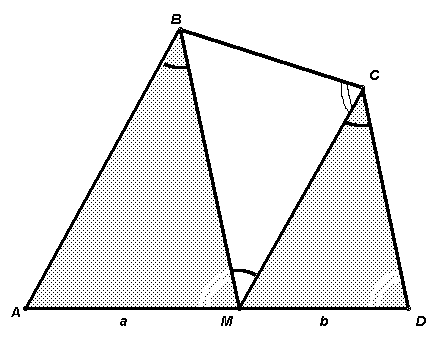

Ответ: ВС = .

Первый способ. Из параллельности прямых ВА и СМ следует, что Р ABM = Р BMC, а из параллельности прямых ВМ и CD следует, что Р BMC = Р DCM и Р AMB = Р MDC (см. рис. 6а). Кроме того, так как АВСD – вписанный четырехугольник, то Р BCM = 180° – Р DCM – Р DAB = 180° – (Р ABM + Р MAB) = Р AMB.

Таким образом, треугольники АВМ, ВМС и МСD подобны (по двум углам). Из подобия первой пары треугольников следует, что , а из подобия второго и третьего треугольников следует, что . Перемножив эти равенства почленно, получим, что , то есть ВС² = ab.

Второй способ. Продолжим прямые ВМ и СМ и отметим точки их вторичного пересечения с окружностью – Е и F соответственно (см. рис. 6б). Получим две вписанные трапеции: ABCF и BCDE. Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая, поэтому ВС = AF = DE.

Используя равенство вписанных углов, опирающихся на одну дугу, и параллельность прямых ВМ и CD, получим: Р DAF = Р FCD = Р ABE = Р ADE и Р AFС = Р ADC = Р AMB = Р DME. Тогда треугольники AFM и DME подобны (по двум углам), следовательно, . Учитывая, что ВС = AF = DE, получим: ВС² = ab.

5.3. (7 баллов) На плоскости отмечены вершины равностороннего треугольника. На каждом шаге разрешается отметить середину отрезка, если его концы также отмечены. Может ли на каком-то шаге оказаться отмеченным центр исходного треугольника?

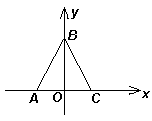
Ответ: нет, не может.

Пусть отмечены вершины равностороннего треугольника АВС. Рассмотрим декартову систему координат на плоскости, начало которой точка О – середина стороны АС, ось абсцисс содержит сторону АС, а ось ординат проходит через вершину В, причем В(0; 1) (см. рис. 7). Тогда ординаты точек А и С равны нулю, а ордината центра исходного треугольника равна .

На каждом шаге отмечается точка, ордината которой равна среднему арифметическому ординат концов отрезка. Поэтому ордината любой вновь отмеченной точки – рациональное число, записываемое обыкновенной дробью со знаменателем вида 2ⁿ, где n – натуральное. Полученное противоречие показывает, что центр данного треугольника не может оказаться отмеченным.