8 класс
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. В дроби ![]() замените звездочку одночленом так, чтобы дробь можно было сократить. Постарайтесь указать как можно больше различных решений.
замените звездочку одночленом так, чтобы дробь можно было сократить. Постарайтесь указать как можно больше различных решений.
Ответ: Приведем две бесконечные серии решений. 1) –2xn – 1, где n – любое натуральное число; 2) x3k – 2, где k – любое натуральное число.
Покажем, что в первом случае дробь можно сократить на (x – 1), а во втором случае – на (x2 + x + 1). Действительно, 1) При n = 1 ![]() =
= ![]() =
= ![]() ;
;
при
n = 2при
n = 3при
n ³ 4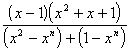 = –
= –2) При
k = 1при
k = 2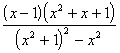 =
= при
k ³ 3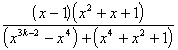 =
= 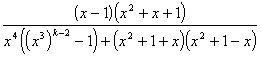 =
= 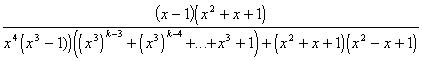 =
= Выполнять сокращение дроби в каждом случае не обязательно, достаточно указать многочлен, на который делится как числитель, так и знаменатель. В частности, в первом случае
x = 1 является корнем многочленов, стоящих в числителе и в знаменателе, поэтому дробь можно сократить на (x – 1). Во втором случае делимость числителя и знаменателя на (x2 + x + 1) можно показать, осуществив деление многочленов «в столбик».Отметим
также, что одночлен (–x2) решением не является, так как в этом случае дробь несократима.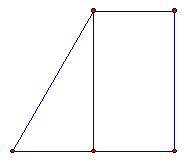
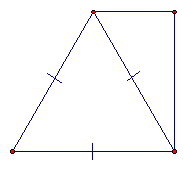
1.2. Существует ли четырехугольник, который можно одной прямой разбить на прямоугольный треугольник и прямоугольник, а другой прямой – на прямоугольный и равносторонний треугольники?
Ответ
: да, существует.Например, прямоугольная трапеция с углом 60° , в которой большая боковая сторона равна большему основанию (см. рис. 1 а, б).
1.3. Найдите наименьшее простое число p, большее двух, такое, что ![]() является точным квадратом.
является точным квадратом.
Ответ: p = 29.
Так как
Отметим, что задачу можно решить и последовательным перебором простых чисел, начиная с
p = 3.
Второй тур (15 минут; каждая задача – 7 баллов
).2.1. На рисунке изображен график функции у = kх + b. В той же системе координат постройте график функции у = bх + k. Поясните ответ.
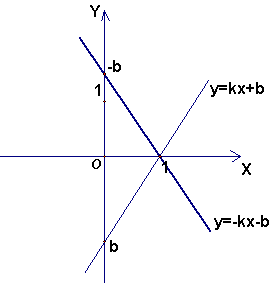
Ответ: см. рис. 2.
Так как точка (1; 0) принадлежит графику функции у = kх + b, то, подставив ее координаты в формулу, получим, что k + b = 0, то есть числа k и b – противоположные. Следовательно, bх + k = –kх – b = –(kx + b).
Таким образом, требуется построить график функции у = –
(kx + b). Этот график симметричен графику функции у = kх + b относительно оси абсцисс (см. рис. 2).2.2. В прямоугольном треугольнике АВС М – середина гипотенузы АВ, N – середина катета АС. Окружность, проходящая через точки М и N, касается катета ВС в точке K. В каком отношении точка K делит этот катет?
Ответ
: 1 : 3.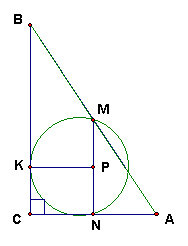
Из условия задачи следует, что М
N – средняя линия треугольника АВС, поэтому МN || ВС иВ четырехугольнике
CKPN есть три прямых угла, поэтому он является прямоугольником. Следовательно, CK = PN =2.3. Число А является суммой трех последовательных натуральных чисел. Число В также является суммой трех последовательных натуральных чисел. Может ли произведение чисел А и В оказаться равным 2007?
Ответ
: нет, не может.Из условия задачи следует, что A = (m – 1) + m + (m + 1) = 3m, где m – натуральное число, отличное от 1. Аналогично, B = 3n, где nÎ N, n ¹ 1. Пусть A× B = 2007, тогда 9mn = 2007 Û mn = 223. Последнее равенство выполняться не может, так как число 223 – простое.
Третий тур (20 минут; каждая задача – 8 баллов
).3.1. Из города в одном направлении выехало три автомобиля: второй – через 10 минут после первого, третий – через 20 минут после второго. Через 30 минут после своего выезда третий автомобиль догнал второй, а еще через 10 минут – первый. Через сколько минут после своего выезда из города второй автомобиль догнал первый?
Ответ
: через 200 минут.Первый способ («алгебраический»). Пусть v1, v2 и v3 – скорости первого, второго и третьего автомобилей соответственно (выраженные, например, в километрах в минуту). Используя скорости сближения автомобилей, составим систему уравнений и преобразуем ее: 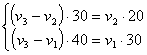 Û
Û
![]() Þ
Þ
![]() .
.
Пусть искомое время равно
t (минут), тогдаВторой способ
(«арифметический»). 1) Так как третий автомобиль выехал через 20 минут после второго, а догнал его еще через 30 минут, то за 30 минут он проезжает такое же расстояние, какое второй проезжает за 50 минут. Следовательно, за 120 минут он проезжает столько же, сколько второй за 200 минут.2) Так как третий автомобиль выехал через 30 минут после первого, а догнал его еще через 40 минут, то за 40 минут он проезжает такое же расстояние, какое первый проезжает за 70 минут. Следовательно, за 120 минут он проезжает столько же, сколько второй за 210 минут.
3) Второй автомобиль выехал через 10 минут после первого и за 200 минут проехал столько же, сколько первый за 210 минут. Значит, через 200 минут после выезда из города второй автомобиль догнал первый.
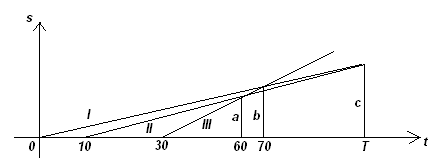
Третий способ («физико-геометрический»)
. Схематически изобразим графики движения автомобилей в одной системе координат в соответствии с условием задачи. Пусть T – время, прошедшее от начала движения до встречи первого и второго автомобилей, а, b и c соответственно – расстояния от города до точек попарных встреч автомобилей (см. рис. 4). Из подобия трех пар прямоугольных треугольников получим: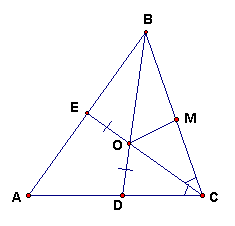
Почленно разделим второе уравнение на первое:
3.2. В треугольнике АВС точка D лежит на стороне АС, биссектриса СЕ пересекается с отрезком ВD в точке О, причем ЕО = DO è Ð EOD = 120° . Найдите угол ВАС.
Ответ
: 60° .Проведем биссектрису ОМ угла
BOC (М – точка ее пересечения со стороной ВС, см. рис. 5). Тогда Ð МОС =Так как Ð ВОС
= 120° , то Ð ОBС + Ð ОСB = 60° , тогда Ð АBС + Ð АСB = 120° , следовательно, Ð BAC = 60° .3.3. Перед боем у Василия Ивановича и Петьки было поровну патронов. Василий Иванович израсходовал в бою в 8 раз меньше патронов, чем Петька, а осталось у него патронов в 9 раз больше, чем у Петьки. Докажите, что исходное количество патронов у каждого делилось на 71.
Пусть Василий Иванович израсходовал x патронов, а у Петьки осталось y патронов. Тогда Петька израсходовал 8x патронов, а у Василия Ивановича осталось 9y патронов. Так как перед боем у обоих было поровну патронов, то x + 9y = 8x + y Û 7x = 8y.
Следовательно,
x делится на 8, то есть x = 8z, где z – натуральное число. Тогда y = 7z, а исходное количество патронов равно x + 9y = 8z + 63z = 71z, то есть делится на 71.
Четвертый тур (25 минут; каждая задача – 9 баллов
).4.1. Пусть ![]() – трехзначное число. Найдите все такие N, для которых N = a + b + c + ab + bc + ca + abc.
– трехзначное число. Найдите все такие N, для которых N = a + b + c + ab + bc + ca + abc.
Ответ
: 199; 299; 399; 499; 599; 699; 799; 899; 999.Преобразуем данное равенство, прибавив к обеим частям по единице
и группируя: N + 1 = a + b + c + ab + bc + ca + abc + 1 Û N + 1 = ab(с + 1) + a(с + 1) + b(с + 1) + (с + 1) = Û N + 1 = (с + 1)(ab + a + b + 1) Û N + 1 = (с + 1)(a(b + 1) + (b + 1)) Û N + 1 = (с + 1)(b + 1)(a + 1).Учитывая, что
N = 100a + 10b + c, где a, b и c – цифры (a ¹ 0), получим: (с + 1)(b + 1)(a + 1) = 100a + 10b + c + 1 Û a(b + 1)(c + 1) + (b + 1)(c + 1) – (c + 1) = 100a + 10b Û a(b + 1)(c + 1) + b(c + 1) = 100a + 10b.Так как
c + 1 £ 10, то b(c + 1) £ 10b. Так как (b + 1)(c + 1) £ 100, то a(b + 1)(c + 1) £ 100a. Таким образом, a(b + 1)(c + 1) + b(c + 1) £ 100a + 10b, причем равенство достигается т., и т. т., когда оно достигается в каждом из двух использованных неравенств, то есть при с = 9 и b = 9 (независимо от значения а).Следовательно,
N – любое трехзначное число, оканчивающееся на 99.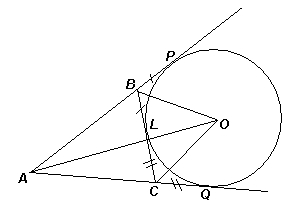
4.2. Дан квадрат АВСD со стороной 1. На стороне ВС взята точка М, а на стороне CD – точка K так, что периметр треугольника MCK равен 2. Найдите угол MAK.
Ответ
: 45° .Первый способ
. Воспользуемся следующим утверждением: если окружность касается стороны ВС и продолжений сторон АВ и АС треугольника АВС в точках Р и Q, то АР = AQ =Это следует из равенства отрезков касательных, проведенных к окружности из одной точки: ВР
= BL и CQ = CL (L – точка касания окружности со стороной ВС). В любом треугольнике существуют ровно три окружности, касающиеся стороны и продолжений двух других сторон. Такие окружности называются вневписанными. Их центры – точки пересечения биссектрис внутреннего угла треугольника и двух внешних углов.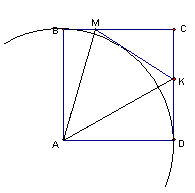
Рассмотрим данный квадрат, треугольник
MCK, описанный в условии, и его вневписанную окружность, касающуюся стороны МK (см. рис. 6б). Так как CB = CD =Так как точка А – центр вневписанной окружности треугольника
MCK, то она является точкой пересечения биссектрис внешних углов M и K этого треугольника.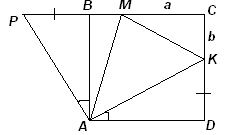
Так как Ð С
MK + Ð СKM = 90° , то Ð BMK + Ð DKM = 270° . Следовательно, Ð МАK = 180° – (Второй способ
. На продолжении стороны СВ данного квадрата отложим отрезок ВР, равный KD (см. рис. 6в).Тогда из равенства прямоугольных треугольников
ADK и ABP следует, что AD = AP и Ð KAD = Ð PAB. Следовательно, Ð PAK = Ð PAВ + Ð ВAK = = Ð KAD + Ð ВAK = 90° .Пусть СМ
= а, CK = b, тогда MK = 2 – (a + b). Кроме того, BM = 1 – a, BP = KD = 1 – b, поэтому, MP = BM + BP = 2 – (a + b). Таким образом, D AMK = D AMP (по трем сторонам), следовательно, Ð МАK = Ð МАP =Отметим, что этот способ решения практически использует поворот с центром А на угол
90° .4.3. От выпуклого n–угольника последовательными прямолинейными разрезами отрезали n треугольников. В результате получился 2007–угольник. Какие значения может принимать n?
Ответ
: все натуральные значения, начиная с n = 1004.
Отрезать треугольник от
n–угольника можно, проведя разрез одним из трёх способов:1) через внутренние точки двух соседних сторон (см. рис. 7а) – тогда количество сторон увеличится на 1;
2) через две вершины, расположенные через одну (см. рис. 7б), – тогда количество сторон уменьшится на 1;

3) через внутреннюю точку стороны и вершину, следующую за концом этой стороны (см. рис. 7в), – тогда количество сторон не изменится.

Таким образом, за
n разрезов можно увеличить или уменьшить количество сторон n–угольника не более, чем на n. Пусть количество сторон увеличилось или уменьшилось на m, тогда n ± m = 2007 Û m = ± (2007 – n). Следовательно, 2007 – n £ n, что равносильно 2n ³ 2007 и n – 2007 £ n, что выполняется при любом натуральном n. Таким образом, nПокажем, что любое найденное значение
n удовлетворяет условию задачи. Действительно, если 1004 £ n < 2007, то сделаем (2007 – n) разрезов первого типа и (2n – 2007) разрезов третьего типа, а если n ³ 2007, то сделаем (n – 2007) разрезов второго типа и 2007 разрезов третьего типа.В обоих случаях будет сделано
n разрезов и получен 2007–угольник.