Математическая регата 11 классов 6.12.2008

1.1. Пусть 0 < x < и 0 < y < . Докажите, что xcosx + ycosy <= ycosx + xcosy.

1.2. Из отрезков с длинами 1, 1, 1, , , составили тетраэдр. Какое наибольшее количество граней может оказаться прямоугольными треугольниками?

1.3. Пусть А – произведение всех простых чисел, не превосходящих 2008, B – произведение всех нечетных чисел, не превосходящих 2008. Найдите предпоследнюю цифру в десятичной записи числа АB.

Второй тур (15 минут; каждая задача — 7 баллов).

2.1. Существует ли многочлен Р(x) ненулевой степени с целыми коэффициентами такой, что = 2008?

2.2. Точка Е лежит на диагонали АС трапеции АВСD. Найдите отношение ее оснований ВС и AD, если площадь треугольника ADE в два раза больше площади треугольника АВЕ.

2.3. Можно ли расставить в вершинах правильного 45-угольника цифры 0, 1, ¼, 9 так, чтобы для любой пары различных цифр нашлась сторона, концы которой занумерованы этими цифрами?

Третий тур (20 минут; каждая задача — 8 баллов).

3.1. Известно, что а <= b <= c <= d <= 0 и a + b + c + d = 1. Найдите наименьшее значение выражения 7a² + 5b² + 3c² + d².

3.2. Внутри квадрата АВСD выбрана точка K такая, что угол KBC равен углу KDB = a. Найдите угол KAD.

3.3. Докажите, что среди любых 39 последовательных натуральных чисел обязательно найдется число, у которого сумма цифр делится на 11.

Четвертый тур (25 минут; каждая задача — 9 баллов).

4.1. При каких b найдутся такие a, что система уравнений 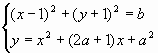имеет хотя бы одно решение?

4.2. В треугольнике ABC: I – центр вписанной окружности, D – середина AB. Найдите , если известно, что угол AID – прямой.

4.3. Имеется набор из двадцати гирь, массы которых выражаются целым числом граммов. Известно, что если из набора удалить любое количество гирь (в том числе и ноль), то оставшиеся гири нельзя будет разложить на две чашки весов так, чтобы они уравновесились. Докажите, что общая масса набора превосходит одну тонну.

Пятый тур (15 минут; каждая задача — 7 баллов).

5.1. Имеет ли уравнение = целые корни?

5.2. В правильной пирамиде РАВСD расстояние от вершины Р до основания АВСD равно половине ребра АВ. Какая из вершин, В или С, находится ближе к прямой РА?

5.3. На плоскости нарисованы красные и синие квадраты, причем множество точек, являющихся вершинами синих квадратов, совпадает со множеством точек, являющихся вершинами красных. Верно ли, что какие-то два квадрата обязательно совпадают?

Результаты регаты: