9 класс
Первый тур (10 минут; каждая задача – 6 баллов).
1.1.
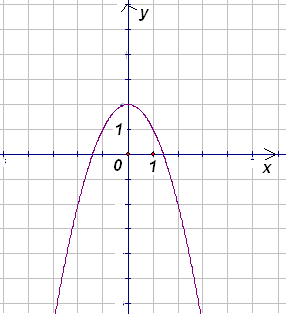
На координатной плоскости изображен график функции y = ax2 + c (см. рисунок). В каких точках график функции y = cx + a пересекает оси координат?Ответ: в точках (0,5; 0) и (0; –1).
Так как данный график пересекает ось y в точке (0; 2), то с = 2. Кроме того, он проходит через точку (1; 1), значит 1 = 2 + а, то есть а = –1.
Таким образом, новая функция задается уравнением y = 2x – 1. Ее график пересекает ось x в точке (0,5; 0), а ось y – в точке (0; –1).
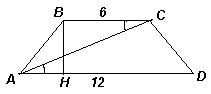
1.2. В равнобокой трапеции AВСD основания AD и ВС равны 12 и 6 соответственно, а высота равна 4. Сравните углы ВАС и САD.
Ответ: угол ВАС больше, чем угол CAD.
Первый способ. Так как AD || BC, то Ð
CAD = Ð
BCA (см. рис. 1а). Пусть BH – высота трапеции. Тогда AH = ![]() = 3; BH = 4, следовательно, из прямоугольного треугольника АВН: AB = 5.
= 3; BH = 4, следовательно, из прямоугольного треугольника АВН: AB = 5.
Таким образом, в треугольнике АBC BC > AB, значит, Ð BAC > Ð BCA (против большей стороны треугольника лежит больший угол). Следовательно, Ð BAC > Ð CAD.
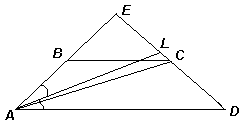
Второй способ. Пусть прямые АВ и CD пересекаются в точке Е (см. рис. 1б). Так как BC || AD и ![]() , то BC – средняя линия треугольника АЕD. Вычислив боковую сторону трапеции (аналогично первому способу решения), получим, что АЕ = 2АВ = 10.
, то BC – средняя линия треугольника АЕD. Вычислив боковую сторону трапеции (аналогично первому способу решения), получим, что АЕ = 2АВ = 10.
Проведем биссектрису AL треугольника АЕD. По свойству биссектрисы ![]() , значит, точка L лежит между точками С и Е. Следовательно, Ð
BAC > Ð
CAD.
, значит, точка L лежит между точками С и Е. Следовательно, Ð
BAC > Ð
CAD.
1.3. На доске записаны числа 1, 21, 22, 23, 24, 25. Разрешается стереть любые два числа и вместо них записать их разность – неотрицательное число. Может ли на доске в результате нескольких таких операций остаться только число 15?
Ответ: да, может.
Искомая последовательность операций видна из следующей записи:
15 = 32 – 16 – (8 – 4 – 2 – 1).
Отметим, что в результате указанных операций можно получить любое нечетное число от 1 до 31. Это можно доказать, например, методом математической индукции.
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Известно, что 5(а – 1) = b + a2. Сравните числа а и b.
Ответ: а > b.
Перепишем условие задачи в виде: b = –a2 + 5a – 5. Выясним знак разности а – b. Получим: а – b = a + a2 – 5a + 5 = (a – 2)2 + 1 > 0. Следовательно, а > b.
Если в системе координат (а; b) построить графики функций b = –a2 + 5a – 5 и b = a, то первый график располагается ниже, чем второй. Исходя из расположения графиков, можно получить ответ, но строгим доказательством это не является.
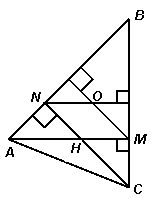
2.2. В остроугольном треугольнике АВС угол В равен 45° , АМ и CN – его высоты, О – центр описанной окружности, Н – ортоцентр (точка пересечения высот). Докажите, что ОNHМ – параллелограмм.
Первый способ. Проведем серединные перпендикуляры к сторонам АВ и ВС данного треугольника, которые пересекаются в точке О (см. рис. 2а). Так как в прямоугольном треугольнике BNC Ð NBC = 45°, то BN = NC, следовательно, точка N лежит на серединном перпендикуляре к стороне BC. Тогда NO || HM. Аналогично, рассмотрев прямоугольный равнобедренный треугольник АМВ, получим, что MO || HN.
Таким образом, ONHM – параллелограмм (по определению).
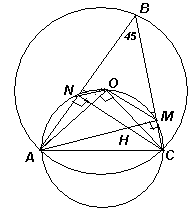
Второй способ. Рассмотрим окружность, описанную около треугольника АВС (см. рис. 2б). Так как этот треугольник – остроугольный, то ее центр O лежит внутри треугольника, причем треугольник АОС – равнобедренный и Ð AOC = 2Ð ABC = 90°. Кроме того, Ð ANC = Ð AMC = 90°, поэтому точки N, O и M лежат на окружности с диаметром AC.
Тогда Ð ONC = Ð OAC = 45°; Ð ONВ = Ð ВNC – Ð ONC = 45° и Ð МАВ = 90° – Ð АВМ = 45°. Из равенства углов ONВ и МАВ следует параллельность прямых NO и AM. Аналогично доказывается, что MO || CN.
Следовательно, ONHM – параллелограмм
2.3. Найдите наименьшее натуральное n, при котором число А = n3 + 12n2 + 15n + 180 делится на 23.
Ответ: n = 10.
Разложим данный многочлен на множители способом группировки: n3 + 12n2 + 15n + 180 = n2(n + 12) + 15(n + 12) = (n + 12)(n2 + 15). Число А делится на простое число 23, если в любом его разложении на натуральные множители присутствует число, делящееся на 23. Наименьшее значение n, при котором первый множитель делится на 23, равно 11, а для второго множителя такое n равно 10.
Возможен также непосредственный перебор всех натуральных значений n от 1 до 10, но он сопряжен с некоторыми вычислительными трудностями. Перебор можно упростить, заменив число 180 на меньшее число, имеющее такой же остаток при делении на 23, например, на –4.
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Пятеро друзей скинулись на покупку. Могло ли оказаться так, что любые два из них внесли менее одной трети общей стоимости?
Ответ: нет, не могло.
Пусть друзья внесли а, b, c, d и е рублей соответственно. Тогда общая сумма внесенных денег равна а + b + c + d + е = ![]() .
.
Предположим, что любые два друга внесли меньше, чем ![]() рублей, тогда выполняются неравенства: а + b <
рублей, тогда выполняются неравенства: а + b < ![]() , а + c <
, а + c < ![]() , ..., d + е <
, ..., d + е < ![]() (всего таких неравенств – десять). Складывая их почленно, получим, что 4(а + b + c + d + е) <
(всего таких неравенств – десять). Складывая их почленно, получим, что 4(а + b + c + d + е) < ![]() , то есть 0,4
, то есть 0,4![]() <
< ![]() Û
1,2
Û
1,2![]() <
< ![]() – противоречие, так как
– противоречие, так как ![]() > 0. Следовательно, указанная ситуация невозможна.
> 0. Следовательно, указанная ситуация невозможна.

3.2. Существует ли прямоугольный треугольник, в котором две медианы перпендикулярны?
Ответ: да, существует.
Пусть в треугольнике ABC: Ð С = 90°, CP и BK – медианы, M – их точка пересечения (см. рис. 3).
Первый способ. Обозначим: BС = a, AC = b, AB = c. Тогда CP = ![]() с; CM =
с; CM = ![]() СР =
СР = ![]() с; BK2 = а2 +
с; BK2 = а2 + ![]() b2; BM2 =
b2; BM2 = ![]() BK2 =
BK2 = ![]() a2 +
a2 + ![]() b2.
b2.
Отрезки CM и BM перпендикулярны тогда и только тогда, когда CM2 + BM2 = BC2, то есть ![]() с2 +
с2 + ![]() a2 +
a2 + ![]() b2 = а2. Учитывая, что с2 = a2 + b2, получим:
b2 = а2. Учитывая, что с2 = a2 + b2, получим: ![]() a2 =
a2 = ![]() b2, то есть b = a
b2, то есть b = a![]() .
.
Таким образом, в прямоугольном треугольнике с катетами CB = a и CA = a![]() . медианы CP и BK перпендикулярны.
. медианы CP и BK перпендикулярны.
Отметим, что медианы прямоугольного треугольника, проведенные к катетам, не могут быть перпендикулярны. Действительно, если AQ – еще одна медиана, то в четырехугольнике CKMQ углы MKC и MQC – острые, а угол KCQ – прямой, значит, Ð KMQ > 90° .
Второй способ. Пусть ![]() ,
, ![]() , тогда
, тогда ![]() ;
; ![]() . Два ненулевых вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю. Значит,
. Два ненулевых вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю. Значит, ![]() =
= ![]() =
= ![]() , так как
, так как ![]() (а и b – модули соответствующих векторов). Следовательно,
(а и b – модули соответствующих векторов). Следовательно, ![]() = 0 Û
= 0 Û
![]() = 0 Û
b = a
= 0 Û
b = a![]() .
.
Заметим, что можно было сразу привести пример требуемого прямоугольного треугольника, указав отношение его катетов или другую тригонометрическую функцию любого из его острых углов, и доказать, что для такого треугольника выполняется перпендикулярность двух медиан. Для этого, в частности, можно было использовать известный факт, что медианы CP и BK перпендикулярны тогда и только тогда, когда с2 + b2 = 5a2.
Возможны также аккуратные рассуждения, использующие понятие непрерывности.
3.3. Какое наибольшее суммарное количество белых и черных шашек можно расставить в клетках доски 8´ 8 так, чтобы выполнялось следующее условие: в каждой горизонтали и в каждой вертикали белых шашек должно быть в два раза больше, чем черных?
|
n |
¡ |
¡ |
¡ |
¡ |
n |
||
|
n |
n |
¡ |
¡ |
¡ |
¡ |
||
|
n |
n |
¡ |
¡ |
¡ |
¡ |
||
|
n |
n |
¡ |
¡ |
¡ |
¡ |
||
|
¡ |
n |
n |
¡ |
¡ |
¡ |
||
|
¡ |
¡ |
n |
n |
¡ |
¡ |
||
|
¡ |
¡ |
¡ |
n |
n |
¡ |
||
|
¡ |
¡ |
¡ |
¡ |
n |
n |
Ответ
: 48 шашек (32 белых и 16 черных).Заметим, что в любой горизонтали не может быть более двух черных шашек (иначе белых будет не менее шести, а в сумме – не менее девяти), значит, белых шашек – не более четырех. Следовательно, всего черных шашек – не более 16, а белых – не более 32.
Один из возможных примеров расстановки 48 шашек, удовлетворяющих условию, – см. рисунок.
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Для различных положительных чисел а и b выполняется равенство ![]() =
= ![]() . Докажите, что а и b – взаимно обратные числа.
. Докажите, что а и b – взаимно обратные числа.
Разобьем правую часть исходного равенства на два одинаковых слагаемых и преобразуем его: ![]() =
= ![]() Û
Û
![]() = 0 Û
= 0 Û
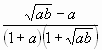 +
+ 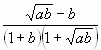 = 0 Û
= 0 Û
![]() –
– ![]() = 0 Û
= 0 Û
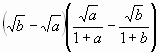 = 0.
= 0.
Первая скобка равна нулю, тогда и только тогда, когда а = b, что противоречит условию. Тогда, учитывая, что а > 0 и b > 0, получим: ![]() = 0 Û
= 0 Û
![]() = 0 Û
= 0 Û
![]() = 0. Последнее равенство верно тогда и только тогда, когда а = b или ab = 1, что и требовалось доказать.
= 0. Последнее равенство верно тогда и только тогда, когда а = b или ab = 1, что и требовалось доказать.
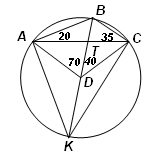
4.2. В выпуклом четырехугольнике ABCD: Ð ВАС = 20° , Ð ВСА = 35° , Ð ВDС = 40° , Ð ВDА = 70° . Найдите угол между диагоналями четырехугольника.
Ответ: 75°.
Докажем, что точка D – центр описанной окружности треугольника ABC. Это можно сделать различными способами.
Первый способ. Опишем окружность около треугольника ABC и продолжим отрезок BD до пересечения с этой окружностью в точке K (см. рис. 4а). Так как Ð ВKС = Ð ВАС = 20°, то Ð KCD = Ð ВDС – Ð DKС = 20° (угол ВDС – внешний для треугольника KDC), следовательно, DC = DK.
Аналогично, так как Ð ВKА = Ð ВСА = 35°, а Ð ВDА = 70° , то Ð KАD = 35°, то есть DK = DA. Таким образом, D – центр окружности, описанной около треугольника ACK, которая совпадает с окружностью, описанной около треугольника ABC.
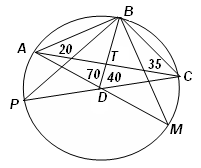
Второй способ. На луче AD отметим точку М так, что отрезок DM = DB (см. рис. 4б). Тогда Ð
DВM = Ð
BMD = ![]() Ð
ВDА = 35° = Ð
ВСА, следовательно, точки A, B, C и M лежат на одной окружности.
Ð
ВDА = 35° = Ð
ВСА, следовательно, точки A, B, C и M лежат на одной окружности.
Аналогично, отметив на луче CD точку Р так, что DP = DB, получим, что точки A, B, C и P лежат на одной окружности. Так как указанные окружности имеют три общие точки, то эти окружности совпадают, кроме того, точка D равноудалена от точек В, М и Р, поэтому она является центром полученной окружности.
Третий способ. Центр описанной окружности тупоугольного треугольника ABC лежит в той же полуплоскости относительно прямой АС, что и точка D (см. рис. 4 а, б). Он является пересечением двух ГМТ: из которых отрезок BC виден под углом a = 2Ð ВАС = 40° и из которых отрезок AB виден под углом b = 2Ð ВСА = 70°.
В указанной полуплоскости эти ГМТ являются дугами окружностей, которые имеют единственную общую точку. По условию, из точки D эти же отрезки видны под такими же углами, поэтому точка D совпадает с центром описанной окружности треугольника ABC.
Теперь ответим на вопрос задачи. Пусть T – точка пересечения диагоналей четырехугольника ABCD (см. рис. 4 а, б). Из равнобедренного треугольника ADB: Ð
DВA = ![]() = 55°; угол BTC – внешний для треугольника BTА, значит, Ð
ВTC = Ð
TАВ + Ð
АВТ = 75°.
= 55°; угол BTC – внешний для треугольника BTА, значит, Ð
ВTC = Ð
TАВ + Ð
АВТ = 75°.
4.3. Найдите все простые числа p, q и r, для которых выполняется равенство:
p + q = (p – q)r.
Ответ: p = 5, q = 3, r = 3.
Из условия задачи вытекает, что p + q делится на p – q, следовательно, (p + q) – (p – q) = 2q также делится на p – q. Если число q – простое, то делителями числа 2q могут являться только числа 1, 2, q и 2q.
Если p – q = 1, то левая часть исходного равенства больше правой. Если p – q = q, то p = 2q, то есть число р – не простое. Аналогично, если p – q = 2q, то p = 3q, то есть и в этом случае, р – не простое число. Значит р – q = 2. Тогда исходное равенство примет вид: (q + 2) + q = 2r Û q + 1 = 2r –1 Û q = 2r – 1 – 1. Далее можно рассуждать по-разному.
Первый способ. Если r = 2, то q = 1 – не простое число. Если r – нечетное число, то (r – 1) – четное, тогда 2r – 1 – 1 делится на 3. Действительно, если kÎ N, то 22k – 1 = 4k – 1 = (4 – 1)(4k – 1 + 4k – 2 + ... +1). Таким образом, q = 3. Тогда р = 5 и r = 3.
Доказывать, что 22k – 1 делится на 3 можно и другими способами, например, методом математической индукции.
Второй способ. Так как q = 2r – 1 – 1 = 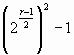 =
= 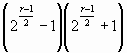 , то q может оказаться простым числом только в случае, когда
, то q может оказаться простым числом только в случае, когда ![]() . Значит,
. Значит, ![]() Û
r = 3. Тогда q = 3 и р = 5.
Û
r = 3. Тогда q = 3 и р = 5.
Пятый тур (15 минут; каждая задача – 7 баллов).
5.1. Найдите наибольшее натуральное n такое, что n200 < 5300.
Ответ: n = 11.
Перепишем данное неравенство в виде: ![]() . Тогда, учитывая, что n – натуральное число, достаточно найти наибольшее натуральное решение неравенства n2 < 125. Так как 112 < 125 < 122, то искомое значение равно 11.
. Тогда, учитывая, что n – натуральное число, достаточно найти наибольшее натуральное решение неравенства n2 < 125. Так как 112 < 125 < 122, то искомое значение равно 11.
5.2. В трапеции ABCD биссектриса тупого угла B пересекает основание AD в точке K – его середине, M – середина BC, AB = BC. Найдите отношение KM : BD.
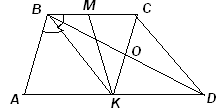
Ответ: KM : BD = 1 : 2.
Так как Ð ABK = Ð CBK = Ð BKA, то треугольник ABK – равнобедренный: AK = AB = BC. Тогда ABCK – параллелограмм (BC = AK, BC || AK), и так как AB = BC, то ABCK – ромб. Так как KD = AK = BC и KD || BC, то BCDK – также параллелограмм.
Пусть O – точка пересечения его диагоналей BD и CK, тогда BO = ![]() BD. Так как треугольник BCK – равнобедренный (BC = CK), то равны его медианы BO и KM, следовательно, KM =
BD. Так как треугольник BCK – равнобедренный (BC = CK), то равны его медианы BO и KM, следовательно, KM = ![]() BD.
BD.
5.3. Существует ли натуральное число, которое при делении на сумму своих цифр как в частном, так и в остатке дает число 2011?
Ответ: нет, не существует.
Предположим, что существует натуральное число n с суммой цифр s, которое удовлетворяет условию задачи. Тогда n = 2011s + 2011, откуда n – s = 2010s + 2011.
Из обоснования признака делимости на 3 следует, что натуральное число и его сумма цифр имеют одинаковые остатки при делении на 3, поэтому n – s делится на 3. Но число 2010s + 2011 на 3 не делится, так как 2010s кратно 3, а 2011 не кратно 3. Следовательно, равенство n – s = 2010s + 2011 выполняться не может, то есть числа n, удовлетворяющего условию задачи, не существует.