10 класс

Первый тур (10 минут; каждая задача – 6 баллов).

1.1. Среднее арифметическое десяти различных натуральных чисел равно 15. Найдите наибольшее значение наибольшего из этих чисел.

Ответ: 105.

Пример: = 15.

Оценка: из условия задачи следует, что сумма данных чисел равна 150. Для того, чтобы одно из слагаемых было наибольшим, необходимо, чтобы остальные девять слагаемых были как можно меньше. Так как все слагаемые должны быть различными, то сумма девяти наименьших из них не может быть меньше, чем 1 + 2 + ... + 9 = 45. Следовательно, наибольшее из данных чисел не может быть больше, чем 105.

1.2. Даны две пересекающиеся плоскости, в одной из которых лежит произвольный треугольник площади. Существует ли его параллельная проекция на вторую плоскость, имеющая ту же площадь?

Ответ: да, существует.

Рассмотрим любой из двугранных углов, образовавшихся при пересечении данных плоскостей, и проведем его биссектор (см. рис. 1). Если проектировать в направлении, перпендикулярном плоскости биссектора, то проекцией любой фигуры будет равная ей фигура (эти фигуры симметричны относительно плоскости биссектора).

Тем самым, условие задачи будет выполнено.

1.3. Дана таблица размером 8×8, изображающая шахматную доску. За каждый шаг разрешается поменять местами любые два столбца или любые две строки. Можно ли за несколько шагов сделать так, чтобы верхняя половина таблицы стала белой, а нижняя половина – черной?

Ответ: нет, нельзя.

Заметим, что обе разрешенные операции не изменяют количество черных и белых клеток в любой строке, следовательно, требуемую раскраску таблицы получить не удастся.

Второй тур (15 минут; каждая задача – 7 баллов).

2.1. Существует ли такой многочлен f(x) степени 6, что для любого x выполнено равенство f(sinx) + f(cosx) = 1?

Ответ: да, существует.

Например, f(x) = –2x⁶ + 3x. Действительно, f(sinx) + f(cosx) = –2sin⁶x + 3sin⁴x – 2cos⁶x + 3cos⁴x = –2(sin⁶x + cos⁶x) + 3(sin⁴x + cos⁴x) = –2(sin²x + cos²x)(sin⁴x – sin²xcos²x + cos⁴x) + 3((sin²x + cos²x)² – 2sin²xcos²x) = –2(1 – 3sin²xcos²x) + 3(1 – 2sin²xcos²x) = 1.

Подобрать такой пример сложно, а получить его можно, например, так: запишем основное тригонометрическое тождество, возведем обе его части в куб, а затем разобьем левую часть полученного равенства на такие две части, чтобы одну из другой можно было получить заменой sinx на cosx. Подробнее: (sin²x + cos²x)³ = 1 ⇔ sin⁶x + 3sin⁴xcos²x + 3sin²xcos⁴x + cos⁶x = 1 ⇔ sin⁶x + 3sin⁴x(1 – sin²x) + 3(1 – cos²x)cos⁴x + cos⁶x = 1 ⇔ (–2sin⁶x + 3sin⁴x) + (– 2cos⁶x + 3cos⁴x) = 1.

Можно получить и другой многочлен. Например, записать равенство sin³3x + cos³3x = 1, возвести обе его части в квадрат и использовать формулы синуса и косинуса тройного угла.

2.2. В квадрате ABCD на стороне ВС взята точка М, а на стороне CD – точка N так, что ∠MAN = 45°. Докажите, что центр окружности, описанной около треугольника AMN, принадлежит диагонали АС.

Первый способ. Проведем окружность c диаметром MN, описанную около треугольника СMN (см. рис. 2а). Пусть она пересекает диагональ АС в точке О, тогда докажем, что О – центр окружности, описанной около треугольника AMN.

Действительно, так как СО – биссектриса угла MCN, то OM = ON. Так как ∠MAN = ∠MON, то окружность с центром О, которая проходит через точки M и N, содержит также и точку А.

В этом способе решения использованы два факта: 1) угол между биссектрисами двух внешних углов треугольника равен 90° – a, где a – противолежащий внутренний угол; 2) следствие из теоремы о «трилистнике» («трезубце»): OI = OM = ON = OA.

2.3. В турнире по игре в «крестики-нолики», проведённом по системе «проиграл – выбыл», участвовали 18 школьников. Каждый день играли одну партию, участников которой выбирали жребием из ещё не выбывших школьников. Каждый из шестерых школьников утверждает, что сыграл ровно четыре партии. Не ошибается ли кто-то из них?

Ответ: ошибается.

Заметим, что всего в турнире было сыграно 17 партий, так как каждый проигравший выбывал. Каждый из шести школьников утверждал, что сыграл по 4 партии, значит, не менее трех из них он должен был выиграть. Так как в каждой партии возможен только один победитель, то в таком случае партий было не меньше, чем 6×3 = 18.

Полученное противоречие показывает, что кто-то из школьников ошибся.

Третий тур (20 минут; каждая задача – 8 баллов).

3.1. Число a – корень уравнения х¹¹ + х⁷ + х³ = 1. При каких натуральных значениях n выполняется равенство a⁴ + a³ = aⁿ + 1?

Ответ: при n = 15.

Так как функция f(x) = х¹¹ + х⁷ + х³ возрастает, то указанное число а – единственный корень уравнения f(x) = 1. Кроме того, f(0) = 0, а f(1) = 3, значит, 0 < a < 1.

Из условия задачи следует, что а¹¹ + а⁷ + а³ = 1. Умножив обе части этого равенства на а⁴, получим: а¹⁵ + а¹¹ + а⁷ = а⁴. Вычтем из этого равенства равенство а¹¹ + а⁷ + а³ = 1, тогда а¹⁵ – а³ = а⁴ – 1 ⇔ a⁴ + a³ = a¹⁵ + 1. Сравнив полученное равенство с равенством a⁴ + a³ = aⁿ + 1, получим, что aⁿ = a¹⁵. Так как 0 < a < 1, то n = 15.

Мы воспользовались тем, что левая часть данного уравнения представляет собой геометрическую прогрессию. Поэтому в решении использован тот же прием, что и при выводе формулы суммы n первых членов геометрической прогрессии.

3.2. В каком отношении делит площадь прямоугольной трапеции, описанной около окружности, биссектриса ее острого угла?

Ответ: в отношении 1 : 1.

Пусть ABCD – данная трапеция c меньшей боковой стороной АВ, тогда биссектриса ее острого угла D проходит через центр О окружности, вписанной в трапецию, и пересекает сторону АВ в точке Е (см. рис. 3 а, б).

Первый способ. Обозначим точки касания вписанной окружности со сторонами АВ, ВС, CD и DA через K, L, M и N соответственно (см. рис. 3а). Заметим, что ∠KOE = ∠ADE < 45° и BKOL – квадрат, поэтому точка Е лежит на отрезке BK.

Так как ∠СDE = ∠ADE = ∠KOE = ∠LOC = ∠MOC (равенство острых углов с соответственно параллельными или с соответственно перпендикулярными сторонами), то ΔOND = ΔOMD и ΔOKE = ΔOLC = ΔOMC (по катету и острому углу). Кроме того, равны квадраты AKON и BKOL.

Таким образом,S_ΔADE = S_ΔOND + S_AKON + S_ΔOKE = S_ΔOMD + S_BKOL + S_ΔOMC = S_ΔOMD + S_BEOL + S_ΔOLC + S_ΔOMC = S_CDEB, то есть биссектриса DE делит площадь данной трапеции пополам.

Второй способ. Пусть радиус вписанной окружности равен r, а ∠СDA = 2α (см. рис. 3а). Тогда S_ABCD = = = = , а S_ΔADE = = = = = = = . Таким образом, , то есть биссектриса DE делит площадь данной трапеции пополам.

Рассмотрим поворот с центром О на 90° по часовой стрелке. Так как AKON и BKOL – равные квадраты (см. рис. 3а), то образом точки А при таком повороте является точка В. Образом луча OF является луч ОЕ, а образом прямой DA – прямая АВ, поэтому точка F при этом повороте переходит в точку Е. Кроме того, образом прямой АВ является прямая ВС, поэтому точка Е переходит в точку С. Таким образом, четырехугольник ОЕВС является образом четырехугольника OFAE, следовательно, эти четырехугольники равны (и равновелики).

Из доказанного следует, что биссектриса DE делит площадь данной трапеции пополам.

3.3. Произведение четырех последовательных положительных нечетных чисел оканчивается на 9. Найдите две предпоследние цифры этого произведения.

Ответ: два нуля.

Среди данных четырех чисел не может быть числа, оканчивающегося на 5 (иначе произведение будет оканчиваться на 5), значит, эти числа оканчиваются на цифры 7, 9, 1 и 3 (именно в таком порядке). Тогда число, лежащее на числовой прямой между вторым и третьим числом, делится на 10, то есть имеет вид 10n (n – натуральное).

Следовательно, произведение данных чисел равно (10n – 3)(10n – 1)(10n + 1)(10n + 3) = (100n² – 9)(100n² – 1) = 10000n⁴ – 1000n² + 9. Заметим, что первые два слагаемых в полученной сумме кратны 1000, поэтому две предпоследние цифры этого числа – нули.

Четвертый тур (25 минут; каждая задача – 9 баллов).

4.1. Решите систему уравнений: .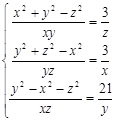

Ответ: ; ; ; .

Преобразуем: 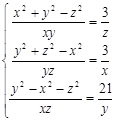⇔ ⇔ Вычтем из первого уравнения второе. Получим: ⇔ ⇔ ⇔ или .

Осталось рассмотреть два случая:

1) . Подставив значение выражения в третье уравнение исходной системы, получим неверное равенство: . Следовательно, этот случай невозможен.

2) . Тогда система, равносильная исходной, после упрощения примет вид: . Учитывая, что z ≠ 0, из первых двух уравнений получим, что y = ±3.

Тогда или ⇔ или или или .

4.2. Вокруг равнобедренного треугольника ABC (AB = AC) описана окружность. Касательная к ней в точке В пересекает луч АС в точке D, Е – середина стороны АВ, Н – основание перпендикуляра, опущенного из точки D на прямую АВ. Найдите длину ЕН, если AD = a.

Ответ: 0,5а.

Первый способ. Отметим середину отрезка AD – точку K (см. рис. 4). Тогда HK – медиана прямоугольного треугольника AHD, проведенная к гипотенузе, значит, HK = AD = 0,5a. Кроме того, KE – средняя линия треугольника ADB, то есть KE || DB.

Пусть ∠ВАС = α, тогда ∠KHA = α (так как KH = KA) и ∠DВС = α (угол между касательной и хордой). Кроме того, ∠СВА = 90° – 0,5α, поэтому ∠KEH = ∠DBH = 90° – 0,5α. Из треугольника KEH: ∠EKH = 180° – (∠KEH + ∠KHE) = 90° – 0,5α = ∠KEH, значит, этот треугольник – равнобедренный, то есть EH = KH = 0,5α.

Второй способ. Пусть ∠BAC = ∠DBC = α, тогда ∠ABC = 0,5α, ∠DBH = 90° - 0,5α (см.рис. 4). Из треугольника ADH: AH = AD cosα = acosα, DH = ADsinα = asinα. Из треугольника BDH: BH = DHctg∠DBH = asinαctg(90° - 0,5α) = 2asin0,5αcos0,5αtg0,5α = 2asin²0,5α.

Следовательно, BE = AB = (AH - BH) = a(cosα - 2sin²0,5&alpha4) = a(1 - 4sin²0,5α); EH = BE + BH = a(1 - 4sin²0,5α) + 2asin²0,5α =a.

4.3. Какое наибольшее число фишек можно расставить в клетках шахматной доски так, чтобы на любой вертикали, на любой горизонтали и на любой диагонали (не только на главных) было чётное число фишек?

Ответ: 48.

Заметим, что на шахматной доске – ровно 16 диагоналей, содержащих нечетное количество клеток (8 «белых» и 8 «черных»). Никакие две из таких диагоналей не имеют общих клеток, поэтому в каждой диагонали хотя бы одна клетка должна остаться пустой. Следовательно, на доске можно расставить не более, чем 64 – 16 = 48 фишек, удовлетворяющих условию.

Один из возможных примеров расстановки 48 фишек – см. рис. 5 (пустыми остаются две главные диагонали).

Пятый тур (15 минут; каждая задача – 7 баллов).

5.1. Найдите наименьшее значение функции f(x) = (a > 0, b > 0, c > 0).

Ответ: .

Рассмотрим отрезок DE длины b. Восставим перпендикуляры к этому отрезку в его концах: DА = a, EВ = c (точки А и В лежат в разных полуплоскостях относительно DE, см. рис. 6). Пусть точка С лежит на отрезке DE и DC = x, тогда ЕС = b – x. Из прямоугольных треугольников ACD и BCE получим: ; .

Так как АС + ВС ≥ AB, то наименьшее значение данной функции равно АВ = (оно достигается, если точка С лежит на отрезке АВ).

Это же решение можно оформить иначе, введя на плоскости декартову систему координат, в которой лучи DA и DE – положительные полуоси y и x соответственно. Тогда А(0; а), В(b; –c); C (x; 0).

При желании можно также найти значение аргумента, при котором достигается искомое значение функции. Так как треугольники ACD и BCE подобны, то ⇔ .

5.2. Сколько сторон может иметь выпуклый многоугольник, у которого сумма тупых углов равна 3000°? (Примеры приводить не надо.)

Ответ: 19 или 20.

Заметим, что выпуклый многоугольник не может иметь более трех не тупых углов (если это не прямоугольник). Действительно, если таких углов больше, чем три, то внешние углы, смежные с ними, – не острые, а это противоречит тому, что сумма внешних углов выпуклого многоугольника (взятых по одному при каждой вершине) равна 360°.

Таким образом, сумма углов данного многоугольника равна 3000° +°, где 0 £ £ 270. Пусть у него n сторон, тогда 180(n – 2) = 3000 +, то есть ⇔ . Учитывая, что n – натуральное число, получим: = 60; n = 19 или = 240; n = 20.

Девятнадцатиугольник, у которого один острый угол величиной 60° и восемнадцать тупых углов с заданной суммой, равно как и двадцатиугольник с тремя острыми углами, сумма которых 240°, и семнадцать тупых углов с заданной суммой, наверняка построить можно, но это построение весьма громоздко, поэтому от учащихся оно не требуется.

5.3. Петя записал на компьютере число 1. Каждую секунду компьютер прибавляет к числу на экране сумму его цифр. Может ли через какое-то время на экране появиться число 123456789?

Ответ: нет, не может.

Первый способ. Предположим, что указанное число может получиться, тогда рассмотрим число x, которое было на экране за секунду до этого. Обозначим сумму цифр числа x через S(x), тогда x + S(x) = 123456789. Заметим, что число 123456789 делится на 9 (так как сумма его цифр делится на 9), а числа x и S(x) имеют одинаковые остатки от деления на 9. Значит, числа x и S(x) также кратны девяти.

Рассуждая аналогично, получим, что и число, из которого получилось x, также должно делится на 9, и так далее. В итоге получим, что исходное число 1 делится на 9, а это неверно. Полученное противоречие показывает, что наше предположение не верно, и число 123456789 появиться на экране не может.

Второй способ. Исходное число имеет остаток 1 при делении на 3. Сумма цифр числа 123456789 равна 45, значит, оно делится на 3. Так как любое число и сумма его цифр дают одинаковые остатки при делении на 3, то при каждой операции остатки от деления на 3 будут удваиваться. Таким образом, последовательность получающихся остатков будет иметь вид: 1; 2; 1; 2; ... . Так как каждое следующий член последовательности зависит только от предыдущего, то она периодична (с периодом 2). Числа 0 в этой последовательности нет, поэтому число, кратное трем, получиться не может.