1.1. Найдите сумму цифр в десятичной записи числа .

Ответ: 8.

Преобразуем: 4^12× 5²¹ = 2^24× 5²¹ = 2^3× 2^21× 5²¹ = 2^3× 10²¹ = 8× 10²¹ = 80…0 (21 нуль). Сумма цифр полученного числа равна 8.

1.2. Диагональ BD параллелограмма ABCD образует углы по 45° со стороной BC и высотой, проведенной из вершины D к стороне АВ. Найдите угол АСD.

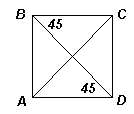
Ответ: 45° .

Из условия задачи следует, что указанная высота параллельна стороне ВС, следовательно, эта высота совпадает со стороной DA, значит, ABCD – прямоугольник (см. рис. 1). Так как ∠АВD = ∠CВD = 45° , то BD – биссектриса угла В этого прямоугольника, значит, ABCD – квадрат. Следовательно, СА – биссектриса угла С квадрата, то есть ∠АСD = 45° .

1.3. Может ли разность квадратов двух простых чисел быть квадратом натурального числа?

Ответ: да, может.

Например, 5² – 3² = 4² или 13² – 5² = 12².

2.1. Для чисел а, b и с выполняется равенство . Следует ли из него, что ?

Ответ: нет, не следует.

Например, при a = c = 1; b = 2 первое равенство выполняется, а второе – нет. Значит, второе равенство не является следствием первого.

2) Из равенства следует, что ⇔ ⇔ ⇔ b² = ac или а = с. Равенство при b ≠ 0 и с ≠ 0 примет вид b² = ac.

Значит, выбрав ненулевые значения переменных так, чтобы а = с и b² ≠ ac, мы получим ситуацию, при которой первое равенство выполняется, а второе – не выполняется.

 

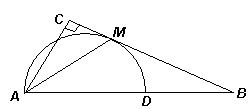
2.2. Полуокружность с диаметром AD касается катета BC прямоугольного треугольника ABC в точке М (см. рисунок). Докажите, что AM – биссектриса угла BAC.

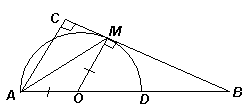
Проведем радиус ОМ данной полуокружности, тогда ОМ = ОА (см. рис. 2). Следовательно, ∠ ОАМ = ∠ ОМА. Кроме того, ОМ^ ВС, значит, ОМ || AC, поэтому ∠ САМ = ∠ ОМА. Таким образом, ∠ ОАМ = ∠ САМ, то есть AM – биссектриса угла BAC.

2.3. Найдутся ли такие три натуральных числа, что сумма любых двух из них – степень тройки?

Ответ: нет, не найдутся.

Пусть нашлись три числа, удовлетворяющие условию. Но среди любых трех чисел найдутся два числа одинаковой четности. Их сумма – четное число, а любая степень тройки – нечетное число.

Полученное противоречие показывает, что требуемых чисел не существует.

3.1. Три математика ехали в разных вагонах одного поезда. Когда поезд подъезжал к станции, математики насчитали на перроне 7, 12 и 15 скамеек. А когда поезд отъезжал, один из математиков насчитал скамеек в три раза больше, чем другой. А сколько скамеек насчитал третий?

Ответ: 7.

Из условия задачи следует, что каждый из математиков в своих подсчетах учел все скамейки на станции ровно по одному разу, то есть в итоге они насчитали равное количество скамеек. Тогда, если после отправления поезда третий математик насчитал n скамеек, то второй должен был насчитать (n + 3) скамейки, а первый – (n + 8) скамеек.

Таким образом, или или . Первые два уравнения не имеют натуральных корней, а решением третьего уравнения является n = 4. Следовательно, всего на станции – 19 скамеек, а математик, о котором спрашивается в задаче, – тот, кто при подъезде к станции насчитал 12 скамеек. Значит, при отъезде от станции он насчитал 7 скамеек.

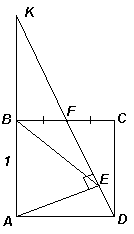
3.2. В квадрате АВСD со стороной 1 точка F – середина стороны ВС, Е – основание перпендикуляра, опущенного из вершины А на DF. Найдите длину ВЕ.

Ответ: 1.

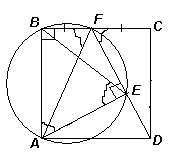
Первый способ. Продолжим отрезок DF до пересечения с прямой АВ в точке K (см. рис. 3а). Прямоугольные треугольники KBF и DCF равны (по катету и острому углу), значит, KB = DC. Таким образом, EB – медиана прямоугольного треугольника АЕK, проведенная к гипотенузе, поэтому ВЕ = AK = 1.

Второй способ. Так как ∠ АBF = ∠ AEF = 90° , то около четырехугольника АВFE можно описать окружность, значит, ∠ ВАF = ∠ СFD (см. рис. 3б).

Проведем отрезок AF, тогда из равенства треугольников АВF и DCF получим, что ∠ СFD = ∠ ВFА. В свою очередь, ∠ ВFА = ∠ ВЕА (вписанные углы, опирающиеся на одну дугу). Таким образом, ∠ ВАF = ∠ ВEА, поэтому треугольник АВЕ – равнобедренный: ВE = АВ = 1.

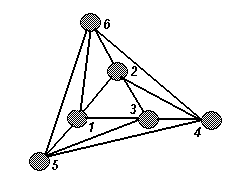
3.3. Можно ли расставить шесть фотографов на площади таким образом, чтобы каждый из них мог сфотографировать ровно четырёх других? (Фотографы А и В могут сфотографировать друг друга, если на отрезке АВ нет других фотографов.)

Ответ: да, можно.

Например, см. рис. 4.

4.1. На диске хранится 2013 файлов размером 1 Мб, 2 Мб, 3 Мб, ..., 2012 Мб, 2013 Мб. Можно ли их распределить по трем папкам так, чтобы в каждой папке было одинаковое количество файлов и все три папки имели один и тот же размер (в Мб)?

Ответ: да, можно.

Первый способ. Заметим, что x + (x + 5) = (x + 1) + (x + 4) = (x + 2) + (x + 3), поэтому 6 файлов, размерами которых в Мб являются шесть последовательных натуральных чисел, можно распределить по трем папкам требуемым образом.

Аналогично, из равенства y + (y + 5) + (y + 7) = (y + 1) + (y + 3) + (y + 8) = (y + 2) + (y + 4) + (y + 6) следует, что 9 файлов, размерами которых в Мб являются девять последовательных натуральных чисел, также можно распределить по трем папкам требуемым образом.

Уравнение 6n + 9m = 2013 ⇔ 2n + 3m = 671 имеет натуральные решения, например, m = 1; n = 334. Это означает, что разбивая числа от 1 до 2013 на одну “девятку” и 334 “шестерки” последовательных натуральных чисел (любым способом) и распределяя соответствующие файлы по трем папкам указанным выше образом, мы получим требуемое распределение.

Второй способ. Возьмём файлы парами и сначала разложим их в три папки следующим образом:

1) 1 + 2013, 4 + 2010, ...

2) 2 + 2012, 5 + 2009, ...

3) 3 + 2011, 6 + 2008, ...

В этих папках будет одинаковое количество файлов и папки будут иметь один и тот же размер. Так как число 2013 при делении на 6 дает остаток 3, то в конце этого процесса останутся три файла с размерами 2014 : 2 = 1007 (Мб), 1006 Мб и 1008 Мб.

Теперь поступим так: положим файл размером 1007 Мб в папку 3), а в папках 1) и 2) поменяем местами файлы размерами 1 Мб и 2 Мб и добавим в них файлы размерами 1006 Мб и 1008 Мб соответственно. Тем самым в каждую папку будет добавлено 1007 Мб и условие задачи будет выполнено.

Отметим, что в результате требуемого распределения каждая из трех папок будет иметь размер : 3 = 675697 (Мб).

4.2. На равных сторонах AB и BC треугольника ABC выбраны точки M и N соответственно так, что AC = CM и MN = NB. Высота треугольника, проведенная из вершины B, пересекает отрезок CM в точке H. Докажите, что NH – биссектриса угла MNC.

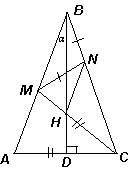
Пусть ∠ АВH = a (см. рис. 5). Так как высота BD данного треугольника является и биссектрисой, то ∠ АВC = 2a . Треугольник BNM – равнобедренный, поэтому ∠ ВMN = ∠ АВC = 2a . Треугольник АСМ – также равнобедренный, значит ∠ CMA = ∠ CAM = 90° – a .

Таким образом, ∠ CMN = 180° – ∠ ВMN – ∠ CMA = 180° – 2a – (90° – a ) = 90° – a . Следовательно, MC – биссектриса угла AMN. Так как BD – биссектриса внутреннего угла треугольника ВMN, а MC – биссектриса его внешнего угла, то точка Н их пересечения является центром вневписанной окружности этого треугольника. Следовательно, NH – биссектриса внешнего угла MNC треугольника ВMN.

4.3. Толя выложил в ряд 101 монету достоинством 1, 2 и 3 копейки. Оказалось, что между любыми двумя копеечными монетами лежит хотя бы одна монета, между любыми двумя двухкопеечными монетами лежат хотя бы две монеты, а между любыми двумя трехкопеечными монетами лежат хотя бы три монеты. Сколько трехкопеечных монет могло быть у Толи?

Ответ: 25 или 26.

Рассмотрим четыре монеты, лежащие подряд. Из условия задачи следует, что среди них не может быть более одной трехкопеечной монеты, более двух двухкопеечных и более двух копеечных монет.

Пусть нашлась такая четверка монет, среди которых вообще нет трехкопеечных, тогда в этой четверке копеечных и двухкопеечных монет должно быть ровно по две. Но это невозможно, так как между любыми двухкопеечными должны лежать две монеты, а копеечные монеты при этом лежать рядом не могут. Таким образом, среди любых четырех монет, лежащих подряд, есть ровно одна трехкопеечная монета.

Так как 101 = 4× 25 + 1, то трехкопеечных монет может оказаться либо 25, либо 26.

Примеры: 1) для 25 монет: 1 3 1 2 | 1 3 1 2 | … | 1 3 1 2 | 1 (25 групп вида 1312 и монета 1); 2) для 26 монет: 3 1 2 1 | 3 1 2 1 | … | 3 1 2 1 | 3 (25 групп вида 3121 и монета 3).