7 класс
Первый тур (10 минут; каждая задача – 6 баллов).
1.1.Два автобуса ехали навстречу друг другу с постоянными скоростями. Первый выехал из Москвы в 11 часов утра и прибыл в Ярославль в 16 часов, а второй выехал из Ярославля в 12 часов и прибыл в Москву в 17 часов. В котором часу они встретились?
Ответ: в 14 часов.
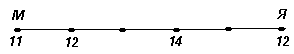
Решение. Так как каждый автобус ехал ровно 5 часов, то за час они проезжают одинаковые расстояния: 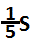 , гдеS– длина пути от Москвы до Ярославля. К тому времени, как выехал второй автобус, первый успел проехать
, гдеS– длина пути от Москвы до Ярославля. К тому времени, как выехал второй автобус, первый успел проехать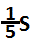 . После этого каждый автобус до встречи преодолел расстояние, равное
. После этого каждый автобус до встречи преодолел расстояние, равное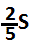 . Следовательно, автобусы встретились через 2 часа после выезда второго, то есть в 14 часов.
. Следовательно, автобусы встретились через 2 часа после выезда второго, то есть в 14 часов.
Это рассуждение можно проиллюстрировать (см. рис. 1). 1.2.В четырёхугольнике ABCD биссектрисы АЕ и СF углов A и C параллельны (см. рисунок). Докажите, что углы B и D равны.
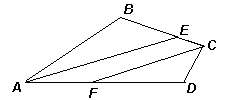
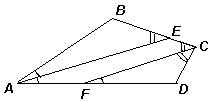 Решение. Из условия задачи и равенства соответственных углов при параллельных прямых следует, что ∠СFD = ∠EAD = ∠EAB и что ∠BEA = ∠BCF = ∠DCF (см. рис. 2). Тогда два угла треугольника АВЕ соответственно равны двум углам треугольника СDF. Следовательно, равны и третьи углы этих треугольников: ∠АВЕ = ∠СDF.
Решение. Из условия задачи и равенства соответственных углов при параллельных прямых следует, что ∠СFD = ∠EAD = ∠EAB и что ∠BEA = ∠BCF = ∠DCF (см. рис. 2). Тогда два угла треугольника АВЕ соответственно равны двум углам треугольника СDF. Следовательно, равны и третьи углы этих треугольников: ∠АВЕ = ∠СDF.
Можно также использовать свойства других углов при параллельных прямых и секущей.
1.3.Можно ли разрезать квадрат 5×5 на прямоугольники двух видов: 1×4 и 1×3 так, чтобы получилось 7 прямоугольников?Ответ: да, можно.
Решение. Например, см. рис. 3.
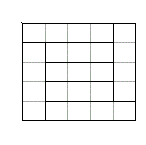
Отметим, что количество прямоугольников каждого вида определяется однозначно, а располагать их можно по-разному. Действительно,пусть x – количество прямоугольников 1×4, тогда прямоугольников 1×3 должно быть 7 – x.Уравнение 4x + 3(7 – x) = 25 имеет единственное решение: x = 4.
Второй тур (15 минут; каждая задача – 7 баллов).
2.1.Банк «Империал» при снятии денег со счета берет комиссию, состоящую из двух частей: фиксированной оплаты за проведение операции и еще оплаты, пропорциональной снятой сумме. Например, при снятии со счета 5000 рублей вкладчик заплатит 110 рублей, а при снятии 11000 рублей заплатит 230 рублей. Какую комиссию заплатит вкладчик, если он захочет снять со счета 8000 рублей?
Ответ: 170 рублей.
Решение. Пусть x рублей – фиксированная оплата, а k – коэффициент пропорциональности. Тогда в первом случае вкладчик заплатит x + 5000k рублей, а во втором случае – (x + 11000k) рублей. Следовательно, 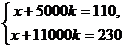 .
.
Решение этой системы: k= 0,02; x= 10. Значит, при снятии 8000 рублей вкладчик заплатит 10 + 8000·0,02 = 170 (р).
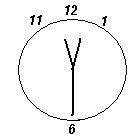
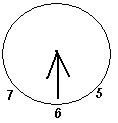
Ответ: 15° или 165°.
Решение. По прошествии часа минутная стрелка вернется в исходное положение, а часовая пройдет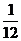 ччасть окружности, то есть повернется на угол, равный 30°. Равенство углов, указанное в условии, означает, что минутная стрелка является либо биссектрисой угла между двумя положениями часовой стрелки (см., например, рис. 4а), либо лучом, дополнительным к этой биссектрисе (см., например, рис. 4б). В первом случае a = 30° : 2 = 15°, а во втором случае a = (360° – 30°) : 2 = 165°.
ччасть окружности, то есть повернется на угол, равный 30°. Равенство углов, указанное в условии, означает, что минутная стрелка является либо биссектрисой угла между двумя положениями часовой стрелки (см., например, рис. 4а), либо лучом, дополнительным к этой биссектрисе (см., например, рис. 4б). В первом случае a = 30° : 2 = 15°, а во втором случае a = (360° – 30°) : 2 = 165°.
2.3.Известно, что остаток от деления некоторого простого числа на 60 равен составному числу. Какому?
Ответ: 49.
Решение. Так как 60 = 22·3·5, то остаток не может быть кратен числам 2, 3 или 5 (иначе исходное число обладало бы тем же свойством и не могло бы оказаться простым). Так как остаток меньше, чем 60, и является произведением хотя бы двух простых множителей, то он равен 7·7 = 49. Другие варианты невозможны так как уже следующее произведение двух простых чисел: 7·11 > 60.
Ситуация, описанная в условии, возможна. Например, 109 = 60·1 + 49, где 109 – простое число.
Третий тур (15 минут; каждая задача – 7 баллов).
3.1.Девять чисел таковы, что сумма любых четырех из них меньше суммы пяти остальных. Докажите, что все числа положительные.
Решение. Разобьем данные числа на две группы: пять самых маленьких и четыре самых больших. Обозначим сумму чисел первой группы через А, а сумму чисел второй – через В, тогда, по условию А>B. Пусть какое-то из данных чисел x≤ 0, тогда оно из первой группы. Перенеся его во вторую группу, заметим, что от этого сумма А не уменьшилась, а сумма В – не увеличилась. Таким образом, знак неравенства не изменился, а это противоречит условию задачи. Следовательно, все данные числа положительные.
Похожее рассуждение можно записать алгебраически. Упорядочим данные числа по возрастанию: а1≤а2≤...≤а8≤а9. По условию а1 + а2 + а3 + а4 + а5 > а6 + а7 + а8 + а9.Пусть а1 ≤ 0,тогда а2 + а3 + а4 + а5 > а6 + а7 + а8 + а9 + а1, что противоречит условию задачи. А так как остальные числа не меньше, чем а1, то они заведомо положительные.
3.2.На сторонах угла ABC отмечены точки М и K так, что углы BMC и BKA равны, BM = BK, AB = 15, BK = 8, CM = 9. Найдите периметр треугольника СOK, где O – точка пересечения прямых AK и СМ.Ответ: 16.
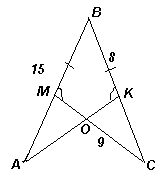
Решение. У треугольников ABK и CBM – общий угол В, поэтому из условия задачи следует, что эти треугольники равны (по стороне и прилежащим углам, см. рис. 5). Тогда ∠BCM = ∠BAK и CB = AB = 15, значит, CK = AM = 7.
Учитывая также, что ∠CKO = ∠AMO (они дополняют равные углы до развернутых), получим, что ΔCOK = ΔAOM (по стороне и прилежащим углам). Следовательно, OK = OM. Таким образом, PΔCOK = CK + CO + OK = CK + CO + OM = CK + CM = 16.
3.3.В некоторой школе в каждом из 20 классов выбрали совет из 5 учеников. Петя оказался единственным мальчиком, избранным в совет класса вместе с четырьмя девочками. Он заметил, что еще в 15 классах девочек выбрали больше, чем мальчиков, хотя в целом по школе мальчиков и девочек выбрано поровну. Сколько мальчиков и сколько девочек в советах четырех оставшихся классов (в сумме)?
Ответ: 19 мальчиков и одна девочка.
Решение. Всего в советы было выбрано 5·20 = 100 человек. Девочек – половина, то есть 50. Если в классе было выбрано больше девочек, чем мальчиков, то девочек выбрано не менее трех. Значит, в 15 классах было выбрано не менее, чем 45 девочек. Еще 4 девочки было выбрано в Петином классе. Так как Петя – единственный мальчик, оказавшийся в совете вместе с четырьмя девочками, то больше ни в одном из классов не могли быть выбраны 4 девочки. Значит, в 16 классах выбрано ровно 49 девочек. Следовательно, в оставшихся четырех классах выбрали 19 мальчиков и одну девочку.
Четвертый тур (20 минут; каждая задача – 8 баллов).
4.1.На листе бумаги были построены система координат (выделена жирно) и графики трех функций:y=ax + b,y=bx+cиy=cx+ a. После этого стерли обозначения и направления осей, а сам лист как-то повернули (см. рисунок). Укажите на рисунке ось абсцисс и ее направление.Ответ обоснуйте.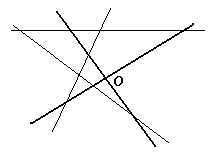
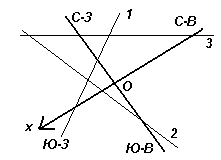
Ответ: см. рис. 6.
Решение.Первый способ. Так как графики попарно пересекаются, то среди чисел а, b и снет одинаковых. Кроме того, коэффициенты в уравнениях переставлены «по циклу», значит, без ограничения общности можно считать, что a < b < c.
Найдем абсциссы точек попарного пересечения графиков и определим их знаки: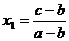 < 0,
< 0,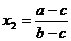 > 0,
> 0,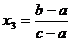 > 0. Выберем полуплоскость, ограниченную одной из осей, в которой располагаются ровно две точки пересечения графиков с положительными абсциссами. Из четырех полуплоскостей она определяется однозначно. Эта полуплоскость ограничена осью ординат и именно в ней лежит положительная полуось абсцисс.
> 0. Выберем полуплоскость, ограниченную одной из осей, в которой располагаются ровно две точки пересечения графиков с положительными абсциссами. Из четырех полуплоскостей она определяется однозначно. Эта полуплоскость ограничена осью ординат и именно в ней лежит положительная полуось абсцисс.
Второй способ. Пронумеруем графики функций, например, так: (1)y = ax + b, (2)y = bx + c, (3)y = cx + a(см. рис. 6). Допустим, что направление на северо-запад является положительным направлением оси ординат. Тогда точки пересечения графиков с этой осью имеют координаты (0; b), (0; c) и (0; а) соответственно, причем a > b > 0 > c. Точки пересечения графиков с другой осью имеют координаты (–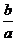 ; 0), (–
; 0), (–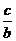 ; 0), (–
; 0), (–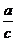 ; 0), где –
; 0), где –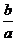 < 0, –
< 0, –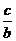 > 0, –
> 0, –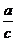 > 0. Отсюда следует, что направление на юго-запад – это положительное направление оси абсцисс, но это противоречит тому, что положительное направление оси абсцисс должно совмещаться с положительным направлением оси ординат поворотом вокруг начала координат против часовой стрелки.
> 0. Отсюда следует, что направление на юго-запад – это положительное направление оси абсцисс, но это противоречит тому, что положительное направление оси абсцисс должно совмещаться с положительным направлением оси ординат поворотом вокруг начала координат против часовой стрелки.
Если же предположить, что положительное направление оси ординат – на юго-восток, то a < b < 0 < c, поэтому знаки рассмотренных абсцисс не изменятся и противоречия не будет. Тем самым ось абсцисс будет направлена на юго-запад.
Два остальных случая возможного направления оси ординат (северо-восток и юго-запад) рассматриваются аналогично и приводят к противоречиям.
4.2.На гипотенузе AB прямоугольного треугольника ABC выбрана такая точка D, что BD = BC, а на катете BC – такая точка E, что DE = BE. Докажите, что AD + CE = DE.
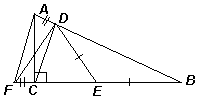 Решение. На продолжении катета ВС за точку С отложим отрезок CF, равный DA (см. рис. 7). Тогда ВА = BF, значит, ∠ВАF = ∠ВFА. Следовательно, равны треугольники DАF и СFА (по двум сторонам и углу между ними), поэтому DF = CA. Тогда равны и треугольники BDF и АСВ (по трем сторонам), значит, ∠BDF = ∠АСВ = 90°. Тогда, из равенства DE = BE следует, что DE – медиана прямоугольного треугольника BDF, проведенная к гипотенузе, то есть DE = BE = FЕ = CF + CE = AD + CE, что и требовалось.
Решение. На продолжении катета ВС за точку С отложим отрезок CF, равный DA (см. рис. 7). Тогда ВА = BF, значит, ∠ВАF = ∠ВFА. Следовательно, равны треугольники DАF и СFА (по двум сторонам и углу между ними), поэтому DF = CA. Тогда равны и треугольники BDF и АСВ (по трем сторонам), значит, ∠BDF = ∠АСВ = 90°. Тогда, из равенства DE = BE следует, что DE – медиана прямоугольного треугольника BDF, проведенная к гипотенузе, то есть DE = BE = FЕ = CF + CE = AD + CE, что и требовалось.
4.3.Верно ли, что изменив одну цифру в десятичной записи любого натурального числа, можно получить простое число?
Ответ: нет, неверно.
Существует много различных контрпримеров. Проще всего рассматривать числа, оканчивающиеся на ноль, для чего удобно использовать понятие факториала натурального числа. (Напомним, чтоn! = 1·2·...·(n – 1)·n.)Приведем три различных контрпримера с соответствующими пояснениями.
Решение. 1) Рассмотрим число 10!. Оно делится на 10, поэтому если изменить любую цифру, кроме последней, то делимость на 10 сохранится. Если последнюю цифру заменить на любую из цифр от 2 до 9, то полученное число будет равно 10! +k(k– последняя цифра). Тогда оно будет делиться наk, так как в рассматриваемое произведение входят все цифры. А если последнюю цифру заменить на 1, то получится число 10! + 1 = 3628801, которое делится на 11 (сумма его цифр, стоящих на нечетных местах, равна сумме цифр, стоящих на четных местах). Таким образом, и в этом случае число не будет простым.
2) Рассмотрим число (10!)3. Изменение любой цифры, кроме последней, а также замена последней цифры на любую цифру от 2 до 9 не дает простого числа по соображениям, изложенным выше. А если последнюю цифру заменить на 1, то получится число (10!)3+ 1, которое можно разложить на множители по формуле суммы кубов: (10!)3+ 1 = (10! + 1)((10!)2– 10! + 1). Значит, и в этом случае число не будет простым.
3) Рассмотрим число 19! + 10. Бесполезность изменения любой его цифры, кроме последней, уже объяснена выше, а замена последней цифры на 1, 2, ..., 9 приведет к тому, что полученные числа будут делиться на 11, 12, ..., 19 соответственно, то есть не будут простыми.