11 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Решите в целых числах неравенство: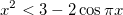 
1.2. В остроугольном треугольнике АВС через центр I вписанной окружности и вершину А провели прямую, пересекающую описанную окружность в точке Р. Найдите IP, если ∠ВАС = α а радиус окружности, описанной около ABC, равен R.
1.3. Существует ли натуральное число, меньшее ста, которое можно представить в виде суммы двух квадратов различных натуральных чисел двумя различными способами?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Могут ли три различных числа вида 2n + 1, где n – натуральное, быть последовательными членами геометрической прогрессии?
2.2. В треугольнике АВС проведена биссектриса АL. О, O1 и O2 – центры описанных окружностей треугольников АВС, АВL и ACL соответственно. Докажите, что ОO1 = ОO2.
2.3. В футбольном турнире в один круг приняли участие 5 команд. В силу погодных условий турнир не был завершен. По результатам проведенных матчей все команды набрали различное количество очков, при этом каждая команда набрала хотя бы очко. Какое наименьшее количество игр могло состояться? (Победа – 3 очка, ничья– 1, поражение – 0.)
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Сумма положительных чисел x, y и z равна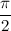 
.
Докажите, что соsx + cosy + cosz > sinx + siny + sinz.
3.2. Дан куб АBCDA’B’C’D’ c ребром 1. На его ребрах АВ, ВС, C’D’ и D’A’ отмечены точки K, L, M и N соответственно так, что KLMN – квадрат. Найдите его площадь.
3.3. Жили-были двадцать шпионов. Каждый из них написал донос на десять своих коллег. Докажите, что не менее, чем десять пар шпионов донесли друг на друга.
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Дан многочлен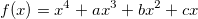 
. Известно, что каждое из уравнений f(x) = 1 и f(x) = 2 имеет четыре корня. Докажите, что если для корней первого уравнения
выполняется равенство x1 + x2 = x3 + x4, то и для корней второго уравнения выполняется аналогичное равенство.
4.2. В треугольнике АВС проведены медиана АМ, биссектриса AL и высота AH. Найдите радиус окружности, описанной около треугольника АВС, если AL = t, AH = h и L – середина отрезка MH.
4.3. Назовем натуральное число убывающим, если каждая цифра в его десятичной записи, кроме первой, меньше или равна предыдущей. Существует ли такое натуральное n, что число 16n – убывающее?
Пятый тур (15 минут; каждая задача – 7 баллов).
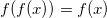, если 
.
положили боком на плоскость и покатили так, что его вершина осталась неподвижна.
Сколько оборотов сделает его основание до момента, когда конус вернется в исходное положение?