10 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Составьте четыре различных четырёхзначных числа, образующих арифметическую прогрессию, используя в каждом числе только цифры 0, 1, 2 и 5, взятые по одному разу.
1.2. Существует ли многогранник, в котором для любых двух вершин найдутся еще две так, чтобы они образовывали квадрат?
1.3. Вася сделал домино, в котором на каждой доминошке – от нуля до семи точек в каждой её половине, причём, как и в обычном домино, присутствуют все варианты и никакие два не повторяются. Сколько доминошек в Васином наборе?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Найдите количество точек плоскости, удовлетворяющих условию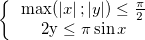 
и имеющих целочисленные координаты.
2.2. Внутри квадрата АВСD расположен квадрат KLMN (в каждом квадрате вершины указаны в одном и том же порядке – по часовой стрелке). Докажите, что середины отрезков AK, BL, CM и DN также являются вершинами квадрата.
2.3. Трехзначное число разделили на его сумму цифр. Какой наибольший остаток мог при этом получиться?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Решите уравнение: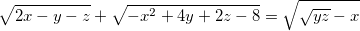 
3.2. На катетах прямоугольного треугольника ABC вне его построены квадраты ACKL и BCMN. Пусть CE – высота треугольника, опущенная на гипотенузу AB. Докажите, что угол LEM – прямой.
3.3. Можно ли покрасить в два цвета боковые рёбра и диагонали основания девятиугольной пирамиды так, чтобы ни один из образовавшихся окрашенных треугольников не был одноцветным? (Рассматриваются только треугольники, вершины которых совпадают с вершинами пирамиды.)
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Решите уравнение: х2 + {х}х + [х] = 0, где [х] и {х} – целая и дробная части числа х соответственно.
4.2. В выпуклом четырехугольнике ABCD точки Е и F – середины сторон ВС и CD соответственно. Найдите наибольшее возможное значение площади треугольника АВD, если площади треугольников ABE, CEF, AEF и AFD образуют в некотором порядке четверку последовательных натуральных чисел.
4.3. Пусть а, b и с – натуральные числа, которые попарно взаимно просты. Какие значения может принимать выражение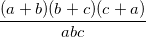 
, если известно, что это число – целое?
Пятый тур (15 минут; каждая задача – 7 баллов).
