10 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Сравните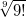 
и 
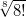. (Напомним, что n! = 1·2·...·n.)
1.2. Каждая сторона треугольника меньше, чем 1. Может ли радиус окружности, описанной около него, быть больше, чем 2019?
1.3. Сколько существует трехзначных чисел, у которых произведение цифр меньше трех?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Решите систему уравнений: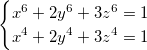 
.
2.2. В угол с вершиной М вписана окружность, которая касается его сторон в точках А и В. АС – диаметр окружности. Прямая, проходящая через точку В параллельно МА, пересекает АС в точке D. В каком отношении прямая СМ делит отрезок BD?
2.3. Шесть участников математического боя сидят за круглым столом. Для улучшения результата они начинают пересаживаться. За одну пересадку меняются местами двое соседей. За какое наименьшее количество пересадок каждый участник сможет посидеть на каждом месте?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Известно, что 5sinβ = sin(2α + β). Найдите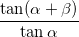 
.
3.2. В прямоугольном параллелепипеде ABCDA’B’C’D’ AB = 3, AD = 4. На ребре DD’ выбрана точка М так, что сечение параллелепипеда плоскостью АС’M является четырехугольником наименьшего периметра. В каком отношении точка М делит ребро DD’?
3.3. Про натуральные числа а и b известно, что дробь 
несократима, а дробь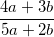 
сократима. На какие натуральные числа она сокращается?
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Для положительных x, y и z докажите неравенство: 4xyz(x + y + z) ≤ (y + z)2(x + z)2
4.2. В правильном треугольнике АВС проведена прямая, параллельная АС и пересекающая стороны АВ и ВС в точках М и N соответственно. Найдите углы треугольника CDE, где D – точка пересечения медиан треугольника ВМN, E – середина отрезка AN.
4.3. В таблице размером 5×5 как-то расставлены числа от 1 до 25. Разрешается менять местами соседние числа в одной строке, если правое больше левого и соседние числа в одном столбце, если нижнее больше верхнего. Можно ли за несколько таких операций получить таблицу, отличающуюся от исходной только тем, что числа в закрашенных клетках (см. рисунок) поменялись местами?
Пятый тур (15 минут; каждая задача – 7 баллов).
