9 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. Существуют ли два целых числа, разность квадратов которых равна 2018?
1.2. Стороны и одна из диагоналей одного четырехугольника соответственно равны сторонам и диагонали другого. Обязательно ли эти четырехугольники равны?
1.3. На бесконечной шахматной доске стоят две фигуры: ладья и ферзь, из которых ни одна не бьет другую. Какое количество клеток может находиться под боем обеих фигур?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. Петя отправился пешком из лагеря в поселок. В 12.00, когда Петя был в а км от лагеря, его нагнал велосипедист, посадил и подвез, высадив в а км от поселка. После этого Петя пришел в поселок в 14.00. Сколько времени потребуется Пете на обратный путь пешком из поселка в лагерь, если известно, что на велосипеде его везли со скоростью вдвое большей, чем он ходит пешком?
2.2. Касательная к описанной окружности треугольника АВС, проведенная в точке В, пересекает прямую АС в точке Р. Окружность с центром Р и радиусом РВ пересекает сторону АС в точке Q. Докажите, что BQ – биссектриса треугольника АВС.
2.3. Найдите все такие натуральные m и n, что 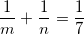 .
.
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Найдите наибольшее значение суммы 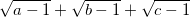 , если a + b + c = 6.
, если a + b + c = 6.
3.2. В треугольнике АВС проведена медиана AD, DP и DQ – биссектрисы треугольников ABD и ACD соответственно, E – точка пересечения AD и PQ. Найдите PQ, если DE = 2.
3.3. Таблицу размером 3×3 надо заполнить числами –1, 0 и 1 так, чтобы суммы чисел в строках были одинаковыми. Сколькими способами это можно сделать? (Способы считаются различными, если различаются полученные таблицы. Все числа использовать не обязательно.)
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Решите уравнение: 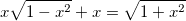
4.2. Три стороны и диагонали одного четырехугольника соответственно равны трем сторонам и диагоналям другого. Обязательно ли эти четырехугольники равны?
4.3. В шахматном турнире по круговой системе (каждый играет с каждым ровно один раз, победа – 1 очко, ничья – 0,5 очка, поражение – 0) каждый из шахматистов, избежавших трех последних мест, половину своих очков набрал во встречах с тремя участниками, занявшими последние три места. Найдите наибольшее возможное количество участников турнира.
Пятый тур (15 минут; каждая задача – 7 баллов).
5.1. Составьте уравнение какого-нибудь приведённого квадратного трёхчлена y = x2 + px + q, график которого пересекает оси координат в вершинах треугольника площади 15.
5.2. Биссектриса угла А треугольника АВС пересекает его описанную окружность в точке D. Серединные перпендикуляры к сторонам АВ и АС пересекают AD в точках М и N соответственно. Докажите, что AM = DN.
5.3. Является ли простым число 16016003?
Результаты регаты:
| Команда | 1 тур | 2 тур | 3 тур | 4 тур | 5 тур | Сумма | Диплом | ||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |||
| ?Летово А | 6 | 0 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 0 | 9 | 9 | 7 | 0 | 7 | 89 | I |
| 1 7 1 (5 4) А | 3 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 3 | 0 | 9 | 3 | 7 | 0 | 7 | 81 | II |
| Летово Б | 6 | 6 | 1 | 7 | 7 | 7 | 8 | 0 | 8 | 9 | 0 | 7 | 7 | 7 | 80 | II | |
| 1 7 9 | 6 | 0 | 6 | 7 | 7 | 7 | 8 | 8 | 7 | 0 | 0 | 9 | 7 | 0 | 7 | 79 | II |
| 2 А | 6 | 0 | 6 | 7 | 7 | 7 | 8 | 8 | 0 | 9 | 9 | 3 | 7 | 0 | 1 | 78 | II |
| 4 4 4 А | 0 | 6 | 6 | 7 | 7 | 7 | 8 | 8 | 8 | 0 | 0 | 0 | 7 | 7 | 0 | 71 | III |
| 1 5 6 8 А | 3 | 6 | 6 | 7 | 7 | 2 | 1 | 6 | 8 | 9 | 0 | 9 | 7 | 0 | 0 | 71 | III |
| ЛНИП А Королёв | 6 | 6 | 6 | 7 | 0 | 0 | 8 | 8 | 8 | 9 | 0 | 5 | 7 | 0 | 0 | 70 | III |
| 2 0 0 7 Б | 6 | 6 | 6 | 7 | 7 | 7 | 1 | 8 | 5 | 0 | 0 | 7 | 0 | 7 | 67 | III | |
| ФТШ С.-Петербург | 6 | 6 | 6 | 7 | 7 | 7 | 1 | 8 | 8 | 0 | 0 | 3 | 0 | 7 | 0 | 66 | III |
| 2 Б | 6 | 0 | 6 | 0 | 7 | 7 | 1 | 8 | 8 | 0 | 9 | 0 | 7 | 6 | 0 | 65 | III |
| 5 А Долгопрудный | 6 | 4 | 6 | 7 | 7 | 4 | 4 | 8 | 8 | 0 | 0 | 9 | 0 | 0 | 0 | 63 | III |
| 3 0 Санкт-Петербург | 6 | 0 | 6 | 7 | 0 | 7 | 8 | 8 | 5 | 0 | 0 | 9 | 7 | 0 | 0 | 63 | III |
| 1 5 1 4 А | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 7 | 5 | 0 | 0 | 0 | 0 | 0 | 0 | 59 | ПП |
| 1 5 4 3 А | 6 | 6 | 6 | 7 | 0 | 6 | 8 | 8 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 55 | ПП |
| Летово В | 6 | 6 | 6 | 7 | 7 | 1 | 8 | 7 | 0 | 0 | 0 | 0 | 0 | 7 | 55 | ПП | |
| 2 0 0 7 А | 5 | 6 | 6 | 7 | 0 | 7 | 1 | 8 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 46 | |
| 1 5 6 8 Б | 6 | 0 | 6 | 7 | 0 | 6 | 2 | 1 | 5 | 4 | 0 | 0 | 0 | 0 | 7 | 44 | |
| 2 0 0 7 Г | 6 | 0 | 0 | 7 | 7 | 0 | 1 | 8 | 8 | 0 | 0 | 0 | 0 | 7 | 0 | 44 | |
| 1 5 1 8 | 6 | 6 | 6 | 7 | 0 | 1 | 1 | 8 | 1 | 0 | 0 | 0 | 0 | 0 | 7 | 43 | |
| 2 0 0 7 Д | 2 | 0 | 6 | 0 | 7 | 0 | 0 | 8 | 6 | 0 | 0 | 0 | 0 | 7 | 7 | 43 | |
| Курчатовская | 3 | 0 | 6 | 7 | 0 | 6 | 0 | 8 | 4 | 0 | 0 | 0 | 0 | 0 | 7 | 41 | |
| 1 5 3 4 Б | 5 | 0 | 0 | 7 | 7 | 0 | 8 | 8 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 38 | |
| ЛНИП Б Королёв | 6 | 0 | 6 | 7 | 0 | 0 | 6 | 8 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 36 | |
| Черноголовка | 0 | 0 | 6 | 7 | 2 | 7 | 0 | 6 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 36 | |
| 5 Б Долгопрудный | 6 | 0 | 0 | 0 | 0 | 7 | 1 | 1 | 1 | 0 | 0 | 5 | 7 | 0 | 7 | 35 | |
| 1 5 6 8 В | 5 | 6 | 6 | 7 | 0 | 0 | 1 | 2 | 8 | 0 | 0 | -1 | 0 | 0 | 34 | ||
| 4 4 4 Б | 3 | 0 | 6 | 7 | 0 | 0 | 0 | 1 | 8 | 0 | 0 | 0 | 0 | 7 | 0 | 32 | |
| 1 5 1 4 Б | 6 | 0 | 0 | 7 | 5 | 2 | 0 | 8 | 1 | 0 | 0 | 0 | 0 | 0 | 3 | 32 | |
| ЛНИП В Королёв | 3 | 0 | 6 | 7 | 0 | 0 | 1 | 2 | 3 | 0 | 0 | 9 | 0 | 0 | 0 | 31 | |
| 1 5 1 1 | 3 | 0 | 6 | 7 | 0 | 0 | 0 | 8 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 28 | |
| 2 1 0 1 Б | 3 | 0 | 6 | 7 | 7 | 0 | 0 | 1 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 27 | |
| 1 7 1 (5 4) Б | 3 | 6 | 1 | 0 | 7 | 0 | 0 | 8 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 26 | |
| 1 5 6 8 Г | 6 | 0 | 0 | 7 | 0 | 0 | 0 | 8 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 25 | |
| Лицей ВШЭ | 4 | 0 | 6 | 1 | 0 | 0 | 0 | 2 | 7 | 0 | 0 | 4 | 0 | 0 | 24 | ||
| 1 7 1 (5 4) В | 3 | 0 | 0 | 7 | 0 | 0 | 1 | 8 | 1 | 0 | 0 | 0 | 0 | 0 | 3 | 23 | |
| 2 0 0 7 В | 1 | 0 | 0 | 0 | 7 | 0 | 1 | 8 | 1 | 1 | 0 | 4 | 0 | 0 | 0 | 23 | |
| 2 В | 4 | 0 | 6 | 0 | 7 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 20 | ||
| 2 1 8 Б | 6 | 0 | 0 | 7 | 0 | 0 | 1 | 2 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 20 | |
| 1 7 1 (5 4) Г | 3 | 0 | 0 | 7 | 0 | 0 | 8 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 19 | ||
| 1 5 3 7 А | 3 | 0 | 0 | 7 | 0 | 0 | 1 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 19 | |
| Покровский кв. А | 6 | 0 | 1 | 7 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | 0 | 0 | 19 | ||
| 1 5 3 7 Б | 3 | 0 | 6 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 7 | 18 | ||
| 1 5 3 4 А | 3 | 0 | 6 | 0 | 0 | 1 | 1 | 2 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 17 | |
| 1 5 4 3 Б | 3 | 6 | 0 | 7 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 17 | ||||
| Мытищи | 3 | 0 | 6 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 17 | |
| 9 1 А | 0 | 0 | 6 | 7 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 16 | |
| 6 4 1 А | 6 | 0 | 0 | 7 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 14 | |||
| Электросталь Б | 3 | 0 | 6 | 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 14 | |
| Электросталь В | 0 | 0 | 6 | 1 | 0 | 2 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12 | |
| 2 1 8 А | 4 | 0 | 6 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | |||
| М М М Ф | 0 | 0 | 1 | 0 | 2 | 0 | 1 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | |
| 1 5 8 1 | 0 | 0 | 1 | 7 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | ||
| Электросталь А | 0 | 0 | 0 | 7 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 9 | |
| Дмитров | 0 | 0 | 6 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8 | |
| Покровский кв. В | 4 | 0 | 0 | 0 | 0 | 0 | 2 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 8 | |
| Покровский кв. Б | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | |
| 2 1 0 1 А | 3 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 6 | ||||
| 6 4 1 Б | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||