10 класс.
Первый тур (10 минут; каждая задача – 6 баллов).
1.1. На координатной плоскости изобразите множество точек, удовлетворяющих условию 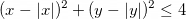
1.2. Площадь треугольника равна 16. Найдите угол между его медианами, длины которых 4 и 6.
1.3. Можно ли раскрасить клетки квадрата размером 6×6 в два цвета так, чтобы клеток одного цвета было больше, чем клеток другого, а в каждом прямоугольнике размером 1×4 было поровну клеток каждого цвета?
Второй тур (15 минут; каждая задача – 7 баллов).
2.1. При делении x2 + 4x – b на x – a получается остаток 2. Найдите наименьшее возможное значение b (а и b – действительные числа).
2.2. Основанием пирамиды с вершиной Р является четырёхугольник ABCD, у которого сумма углов А и D в пять раз меньше суммы углов B и C. Найдите угол между плоскостями граней PAB и PCD, если они обе перпендикулярны основанию.
2.3. По кругу лежат 10 монет орлами вверх. Разрешается одновременно перевернуть либо 4 монеты, лежащие подряд, либо 4 монеты, лежащие по две с обеих сторон от какой-то монеты. Можно ли в результате таких операций положить все монеты орлами вниз?
Третий тур (20 минут; каждая задача – 8 баллов).
3.1. Имеет ли ненулевые рациональные решения уравнение x3 + x2y + y3 = 0?
3.2. Выпуклый n-угольник разрезан на квадраты и правильные треугольники. Докажите, что n≤12.
3.3. Рассматриваются всевозможные пятизначные числа, в десятичной записи которых цифры убывают. Каких из них больше: с суммой цифр 22 или с суммой цифр 23?
Четвертый тур (25 минут; каждая задача – 9 баллов).
4.1. Существует ли такая бесконечная последовательность квадратов натуральных чисел, что для любого натурального n сумма первых n ее членов также является квадратом натурального числа?
4.2. На сторонах АВ и ВС треугольника АВС отмечены произвольные точки М и K соответственно, О – середина отрезка MK. Докажите, что АО + СО > АМ + CK.
4.3. На каркасе единичного куба находятся восемь муравьев. Докажите, что найдутся два муравья, расстояние между которыми не больше, чем 1.
Пятый тур (15 минут; каждая задача – 7 баллов).
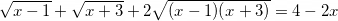 .
.