1. Один из пяти мальчиков разбил стекло. При разбирательстве у директора Андрей сказал: "Это не я, не Боря и не Вася". Боря: "Это не я, не Вася и не Гриша". Вася: "Это не я, не Гриша и не Дима". Гриша: "Это не я, не Дима и не Андрей". Дима: "Это не я, не Андрей и не Боря". Сколько мальчиков сказали неправду? (И. Рубанов)
2. У двух хулиганов есть учебник, в котором 300 страниц, занумерованных по порядку числами от 1 до 300 (всего 150 листов). Они играют, по очереди вырывая из учебника по одному листу. Цель того, кто вырывает лист первым, - получить число 100 в виде суммы нечетных номеров некоторых вырванных им страниц. Цель второго игрока - получить число 100 в виде суммы четных номеров некоторых вырванных им страниц. Побеждает тот, кто первым достигнет своей цели. Кто из хулиганов выиграет при правильной игре обоих? (С. Волченков)
3. В каждый из трех сосудов налили по целому числу литров воды. После этого из каждого сосуда отлили по целому числу литров воды. При этом оказалось, что из первого сосуда отлили 10% содержавшейся в нем воды, из второго сосуда - 15% содержавшейся в нем воды, из третьего сосуда - 20% содержавшейся в нем воды, а общее количество воды во всех сосудах уменьшилось на 18%. Какой наименьший объем воды мог содержаться в третьем сосуде? (По мотивам задачи с омских олимпиад)
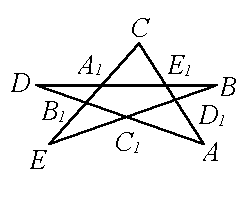
4. В пятиконечной звезде (см. рис.)
/DAC+/EA1B=/EBD+/CB1A=/ECA+/DC1B=/ADB+/ED1C =/CEB+/DE1A=144o.
Докажите, что /DAC=/EBD=/ECA=/ADB=/CEB.
(Р. Исмаилов)

5. На белом листе клетчатой бумаги нарисовали квадрат размером 12*12. Две клетки считаются соседними, если у них есть общая сторона. Саша закрашивает по одной клетке, вписывая в каждую закрашенную клетку число ранее закрашенных ее соседей. Чему будет равна сумма всех чисел, когда будут закрашены все клетки? (А. Шаповалов)
6. Как разрезать произвольный прямоугольник на две части, из которых можно сложить шестиугольник с равными сторонами? (Жюри)
1. Ваня и Федя живут в поселках, между которыми по прямому шоссе 30 км, а их дядя - на том же шоссе ровно посередине между ними. Дядя пригласил племянников в гости. У него есть мотороллер, скорость которого 20 км/ч. Для экономии времени все стартуют одновременно: ребята выходят пешком, а дядя выезжает на мотороллере, по очереди подбирает племянников на дороге и подвозит к себе домой. За какое наименьшее время все могут добраться до дома дяди, если Ваня ходит со скоростью 4 км/ч, а Федя - 5 км/ч? (А. Шаповалов)
2. У двух хулиганов есть учебник, в котором 300 страниц, занумерованных по порядку числами от 1 до 300 (всего 150 листов). Они играют, по очереди вырывая из учебника по одному листу. Цель того, кто вырывает лист первым, - получить число 100 в виде суммы нечетных номеров некоторых вырванных им страниц. Цель второго игрока - получить число 100 в виде суммы четных номеров некоторых вырванных им страниц. Побеждает тот, кто первым достигнет своей цели. Кто из хулиганов выиграет при правильной игре обоих? (С. Волченков)
3. Можно ли расставить в таблице 4*6 различные натуральные числа, не превосходящие 30, так, чтобы каждая пара чисел в клетках с общей стороной имела общий делитель, больший единицы? (А. Шаповалов)
4. В параллелограмме АВСD стороны АВ = 4, ВС = 7. Биссектрисы АK и ВМ углов параллелограмма пересекаются в точке О (точки K и M принадлежат сторонам ВС и АD соответственно). Найдите отношение площадей SОКСDM и SОАВ. (Нижегородские олимпиады)
5. На белом листе клетчатой бумаги нарисовали квадрат размером 12*12. Две клетки считаются соседними, если у них есть общая сторона или общая вершина. Саша закрашивает по одной клетке, вписывая в каждую закрашенную клетку число ранее закрашенных ее соседей. Чему будет равна сумма записанных чисел, когда все клетки будут закрашены (перечислите все возможности)? (А. Шаповалов)
6. В городе Глупове 200000 домов и каждый из них имеет свой собственный номер. Оказалось, что из-за плохого почерка почтальоны иногда путают номера. Тогда мэр распорядился присвоить домам такие номера, чтобы любые два номера отличались, по крайней мере, в двух разрядах, и наибольший используемый номер был как можно короче. Сколько цифр будет в записи этого номера? (С. Волченков)
1. Графики функций y=ax+a и y=bx+b пересекаются в единственной точке M. Докажите, что график функции y=cx+d проходит через точку M тогда и только тогда, когда c=d. (Д. Кузнецов)
2. В теннисном турнире "на вылет" (после первого поражения участник выбывает из турнира) для победы в игре надо выиграть у соперника три сета. После турнира один из его участников утверждал, что он выиграл 17 сетов и проиграл 14 сетов. Докажите, что он говорил неправду. (А. Храбров)
3. На плоскости даны два треугольника одинаковой площади. За один ход разрешается, оставляя на месте две вершины треугольника, сместить третью его вершину так, чтобы площадь треугольника не изменилась. Докажите, что за несколько таких операций можно из первого данного треугольника получить второй. (С. Волченков)
4. Из квадрата n*n по клеточкам вырезали n "доминошек" (прямоугольников 1*2), покрывающих все клетки главной диагонали. В результате квадрат распался на две фигуры - Ф1 и Ф2. Докажите, что эти фигуры можно разрезать на доминошки тогда и только тогда, когда в них поровну клеток. (Д. Карпов)
5. С натуральным числом, написанным на доске, разрешается проделать такую операцию: умножить его на выражение (p-1)2/p, где p - его простой делитель, и записать результат вместо исходного числа. Докажите, что, какое бы исходное число мы ни взяли и как бы мы ни проделывали описанные операции, на доске рано или поздно появится число 1. (А. Шаповалов)
6. Точка K - середина стороны ВС квадрата ABCD. На отрезке AK взята такая точка E, что СЕ = ВС. Найдите угол АЕD. (Д. Кузнецов)
1. Петя умножает число 1998 на правильную дробь так, чтобы результат оказался снова натуральным числом. С результатом он проделывает то же самое, и т.д. Какое наибольшее количество умножений он может проделать? (С. Волченков)
2. В теннисном турнире "на вылет" (после первого поражения участник выбывает из турнира) для победы в игре надо выиграть у соперника три сета. После турнира один из его участников утверждал, что он выиграл 17 сетов и проиграл 14 сетов. Докажите, что он говорил неправду. (А. Храбров)
3. Можно ли записать натуральное число и его квадрат, использовав каждую из десяти цифр 0, 1, ..., 9 ровно один раз? (С. Токарев)
4. Картонный треугольник разрезали по прямой на две части, одну из получившихся частей опять разрезали на две, и так далее. После восьми разрезов оказалось, что одна из получившихся частей - десятиугольник. Какими могут быть остальные части (укажите все возможные варианты).
5. Два игрока по очереди красят непокрашенные стороны 43-угольника таким образом, чтобы никакие две соседние стороны не были покрашены в один цвет. Проигрывает тот, кто последним ввел в игру новый цвет. Кто из игроков может обеспечить себе победу?
6. Из квадрата 12*12 по клеточкам вырезали 12 "доминошек" (прямоугольников 1*2), покрывающих все клетки главной диагонали. В результате квадрат распался на две фигуры ("верхнюю" и "нижнюю"), состоящие из 60 клеток каждая. Докажите, что эти фигуры можно разрезать на доминошки. (Д. Карпов)