
Условия задач
1. Найдите все тройки натуральных чисел, таких, что сумма чисел каждой тройки равна 1996, а сумма любых двух из них кратна третьему.
2. Можно ли разбить квадрат на треугольники так, чтобы каждый треугольник граничил (по отрезку) не менее чем с четырьмя другими?
3. Трое ребят играли в слова. Каждый составил по 10 слов. Если слово есть у всех, оно вычеркивается, если ровно у двоих - оба получают по одному очку, за остальные свои слова каждый получает по три очка. В итоге все трое набрали разное количество очков, меньше всех - 19 очков - набрал Кузя. По сколько очков набрали остальные игроки?
4. Если (b/(a(a+b))) + (c/(b(b+c)))+ (a/(c(c+a))) - целое число, то (a/(b(a+b))) + (b/(c(b+c)))+ (a/(c(c+a))) - целое число. Доказать.
5. В равнобедренной трапеции ABCD диагонали пересекаются в точке E. Через концы боковой стороны AB и точку E проведена окружность с центром O. Докажите, что OE | CD.
6. Можно ли так расставить шахматных коней на бесконечной клетчатой доске, чтобы любые две соседние клетки находились под боем различного числа коней? (Соседними называются клетки, имеющие одну или две общих вершины.)
7. Числа a и b таковы, что ab<0, число с - произвольно. Докажите, что a2+b2+c2 >2(ab+ac+bc) .
8. На доске выписаны все целые числа от 1 до 14, каждое - по одному разу. Двое играющих по очереди стирают по одному числу до тех пор, пока не останется ровно два числа. Если их сумма - точный квадрат, то выигрывает второй, иначе - первый. Кто выигрывает при правильной игре?
9. Внутри прямого угла Х взята точка Р. Рассмотрим всевозможные прямоугольные треугольники АРВ, у которых концы гипотенузы А и В лежат на сторонах угла Х. Какую фигуру образуют на плоскости середины отрезков AB ?
10. Можно ли из бесконечной клетчатой плоскости удалить такие два непересекающихся "луча" ("лучом" называются клетки одной строки или одного столбца, идущие подряд, начиная с некоторой клетки плоскости), чтобы, начав с некоторой неудаленной клетки, обойти всю оставшуюся плоскость? Разрешается переходить из любой клетки плоскости на любую соседнюю по горизонтали или вертикали неудаленную клетку, которая не была пройдена ранее.
1. Компьютер печатает значения выражения n2-13n+47 при всех n = 1, 2, ..., 10000. Какое наибольшее количество простых чисел он может напечатать подряд?
2. На сторонах AB, BC, CA треугольника ABC взяты точки K, L, M соответственно так, что AK:KB=BL:LC=CM:MA=1:2. Докажите, что точки пересечения медиан треугольников ABC и KLM совпадают.
3. Семиклассник разрезал бумажный квадрат на прямоугольники периметра 7 см, а восьмиклассник - точно такой же квадрат на прямоугольники периметра 8 см. Может ли у восьмиклассника получиться больше прямоугольников?
4. На белой доске размером 4*n двое по очереди красят по одной клетке, причем никакие две закрашенные клетки не должны граничить между собой по вертикали, горизонтали или диагонали и никакую клетку нельзя красить второй раз. Проигрывает тот, кто не может сделать очередной ход без нарушения правил. Кто выигрывает при правильной игре: тот, кто делает первый ход, или его партнер?
5. На рисунке справа изображен план города Туманного. Из-за
постоянных туманов видимость в городе составляет половину стороны квартала.
По принятым в городе правилам с каждого перекрестка можно ехать только по
улицам, идущим на схеме вверх или вправо. Какое наименьшее число постов ГАИ
надо расставить на перекрестках, чтобы по их отчетам можно было точно
восстановить маршрут автомобиля, проехавшего из левого нижнего угла схемы в
правый верхний и не нарушавшего правил?

6. С конечной последовательностью нулей и единиц разрешается производить следующую операцию: заменять 01 на 10...0 (число нулей на каждом шаге произвольно). Может ли для некоторой начальной последовательности процесс замен продолжаться бесконечно?
7. В фирме "Рога и копыта" работают 1111 сотрудников. По распоряжению мэра Черноморска каждый сотрудник должен в течение года отработать 7 дней подряд на благоустройстве городской территории. Докажите, что в течение этого года найдется семь дней (не обязательно идущих подряд), когда благоустройством занималось нечетное число работников фирмы.
8. Петя написал наименьшее натуральное число вида aa...a, которое кратно 1996. Чему равно а ?
9. Выпуклый семиугольник вписан в окружность единичного радиуса. Докажите, что сумма длин всех его сторон и диагоналей меньше 33.
10. Разложите многочлен x8+98x4y4+y8 в произведение двух многочленов с целыми коэффициентами.
МАТЕМАТИЧЕСКИЙ БОЙ N 3. 21.02.1996. ВЫСШАЯ ЛИГА
1. Угол при вершине A равнобедренного треугольника ABC равен 100o. На продолжении боковой стороны AB за точку B взята такая точка D, что AD=BC. Найдите величину угла ADC.
2. Пусть а, b и с - положительные числа, а2+b2+c2 = 1. Докажите, что b(a+c) < 21/2/2.
3. В классе 28 учеников, которые сидят по двое за партами. Каждый день учитель пересаживает учеников так, чтобы все образовавшиеся пары были новыми (раньше рядом не сидели). Может ли он делать это в течение 27 дней?
4. Два игрока по очереди красят клетки доски 3*3. Вначале все клетки белые. Первый игрок красит клетки в красный, а второй - в синий цвет. За один ход каждый может закрасить не более трех клеток, из которых не более одной небелой. Первый игрок хочет получить красный квадрат 2*2. Может ли второй ему помешать?
5. В равнобедренном треугольнике ABC (AB=BC) проведена биссектриса AD. При каких значениях угла A на прямой AC существует такая точка E, что BD=DE=EC?
6. Докажите, что при любом натуральном n>4 можно разбить все целые числа от 1 до n на две группы так, чтобы сумма всех чисел одной группы равнялась произведению всех чисел другой?
7. Поверхность кубика 3*3*3 разлинована на единичные квадратики. Какое наибольшее число квадратиков можно закрасить так, чтобы среди них не было двух, имеющих общую сторону?
8. Найдите все такие пары положительных рациональных чисел a и b, что оба числа a+b+(1/(ab)) и ab+(1/a)+(1/b) - целые.
9. На доске выписаны числа 1, 2, :, 1000000. На каждом этапе одновременно стираются все числа, имеющие среди нестертых чисел ровно один делитель (например, на первом этапе стирается только число 1). Какие числа будут стерты на последнем этапе?
10. Шахматная фигура "лебедь" может ходить на только клетки, расположенные по отношению к ее клетке так, как показано на рисунке справа. Эта фигура, начав с одной из угловых клеток доски, обошла ее, побывав на каждой клетке ровно по одному разу. На какой из двух диагоналей доски могла быть расположена исходная клетка?
1. Можно ли так расставить шахматных коней на бесконечной клетчатой доске, чтобы любые две различные клетки в любом квадрате 3*3 находились под боем разного числа коней?
2. Четыре персонажа басни Крылова и коза-баянистка задумали сыграть квинтет. Все пятеро уселись в кружок, однако музыка не пошла. Тогда они стали пересаживаться. За одну пересадку меняются местами двое соседей. Герои не успокоятся, пока каждый не посидит на каждом месте. Какое наименьшее число пересадок им понадобится?
3. Двое играют в следующую игру. Вначале у каждого из них имеется по 100 однокопеечных, по 80 двухкопеечных, по 60 трехкопеечных и по 40 пятикопеечных монет. Игрок, чья очередь делать ход, выбирает одну из своих монет и передает ее сопернику. Если соперник может разменять эту монету на более мелкие, он обязан сделать это, после чего сам делает очередной ход. Если же соперник не может разменять эту монету, он все равно оставляет ее себе, но очередность хода при этом не изменяется. Начинающий игрок выигрывает, если после очередного хода у него не останется ни одной монеты. Сможет ли второй игрок ему помешать?
4. Найдите все такие тройки простых чисел p, q, r, для которых p+q+r+pq+qr+pr+pqr = 19961995.
5. В четырехугольнике ABCD углы A и C - прямые, а угол ADB в два раза больше угла BDC. Точка K такова, что точка C - середина отрезка BK, а O - точка пересечения диагоналей четырехугольника ABCD. Найти величину угла KOD.
6. В выпуклом пятиугольнике площади S соединены середины соседних сторон. Докажите, что площадь получившегося пятиугольника больше S/2.
7. Известно, что три из шести чисел a, b, c, d, e, f равны 1, а остальные три равны 0. Разрешается написать список из четырех вопросов типа: "Чему равна сумма таких-то чисел?" (список может содержать любой набор вопросов, вопрос может содержать любой набор неповторяющихся слагаемых). Можно ли составить этот список так, чтобы, получив ответы на все входящие в него вопосы, однозначно определить все числа?
8. С конечной последовательностью нулей и единиц разрешается производить следующие операции: заменять 01 на 100 или на 110. Может ли для некоторой начальной последовательности процесс замен продолжаться бесконечно?
9. Докажите, что для любых неотрицательных x и y справедливо неравенство 3x2y+2y2x+8x+3y > 14xy.
10. Каждая клетка доски 10*10 покрашена в черный или белый цвет. За один ход перекрашиваются в противоположный цвет все черные клетки, имеющие 0, 1, 4, 5, 6, 7 или 8 черных соседей, а также все белые клетки, у которых ровно три черных соседа. Верно ли, что для каждого расположения клеток существует предшествующее ему, то есть такое, из которого его можно получить за один ход?
1. Найдите все тройки натуральных чисел, таких, что сумма чисел каждой тройки равна 1996, а сумма любых двух из них кратна третьему.
2. Можно ли разбить квадрат на треугольники так, чтобы каждый треугольник граничил (по отрезку) не менее чем с четырьмя другими?
3. Трое ребят играли в слова. Каждый составил по 10 слов. Если слово есть у всех, оно вычеркивается, если ровно у двоих - оба получают по одному очку, за остальные свои слова каждый получает по три очка. В итоге все трое набрали разное количество очков, меньше всех - 19 очков - набрал Кузя. По сколько очков набрали остальные игроки?
4. Катеты AB и AC равнобедренного прямоугольного треугольника ABC равны 1. Окружность, вписанная в угол BAC, делит гипотенузу AC на 3 равные части. Найдите радиус окружности.
5. Числа a и b таковы, что ab<0, число с - произвольно. Докажите, что a2+b2+c2 > 2(ab+ac+bc) .
6. В равнобедренной трапеции ABCD диагонали пересекаются в точке E. Через концы боковой стороны AB и точку E проведена окружность с центром O. Докажите, что OE | CD
7. Можно ли так расставить шахматных коней на бесконечной клетчатой доске, чтобы любые две соседние клетки находились под боем различного числа коней? (Соседними называются клетки, имеющие одну или две общих вершины.)
8. Из пункта A в пункт B выехал с постоянной скоростью велосипедист. Одновременно с ним из пункта B в пункт A вышли с постоянными скоростями два пешехода, причем скорость первого больше скорости второго пешехода в полтора раза. Велосипедист встретился с первым пешеходом через 5 часов, а со вторым - еще через 50 минут. Найдите отношения скоростей велосипедиста и пешеходов.
9. На доске выписаны все целые числа от 1 до 14, каждое - по одному разу. Двое играющих по очереди стирают по одному числу до тех пор, пока не останется ровно два числа. Если их сумма - точный квадрат, то выигрывает второй, иначе - первый. Кто выигрывает при правильной игре?
10. Можно ли из бесконечной клетчатой плоскости удалить такие два непересекающихся "луча" ("лучом" называются клетки одной строки или одного столбца, идущие подряд, начиная с некоторой клетки плоскости), чтобы, начав с некоторой неудаленной клетки, обойти всю оставшуюся плоскость? Разрешается переходить из любой клетки плоскости на любую соседнюю по горизонтали или вертикали неудаленную клетку, которая не была пройдена ранее.
1. Семиклассник разрезал бумажный квадрат на прямоугольники периметра 7 см, а восьмиклассник - точно такой же квадрат на прямоугольники периметра 8 см. Может ли у восьмиклассника получиться больше прямоугольников?
2. На белой доске размером 4*n двое по очереди красят по одной клетке, причем никакие две закрашенные клетки не должны граничить между собой по вертикали, горизонтали или диагонали и никакую клетку нельзя красить второй раз. Проигрывает тот, кто не может сделать очередной ход без нарушения правил. Кто выигрывает при правильной игре: тот, кто делает первый ход, или его партнер?
3. С конечной последовательностью нулей и единиц разрешается производить следующую операцию: заменять 01 на 10...0 (число нулей на каждом шаге произвольно). Может ли для некоторой начальной последовательности процесс замен продолжаться бесконечно?
4. Можно ли так покрасить конечное число клеток бесконечного клетчатого листа, чтобы каждая покрашенная клетка имела ровно 5 покрашенных соседей?
5. По окружности в произвольном порядке расставлены цифры от 1 до 9 (каждая - ровно один раз). Начиная с любой цифры, по часовой стрелке прочитываем трехзначное число. Чему может равняться сумма этих девяти чисел?
6. Вначале на доске написаны числа 1, 9, 9, 6, и только они. Разрешается выбрать из написанных на доске чисел три произвольных числа a, b и c и дописать на доску три числа a(b+c), b(c+a) и c(a+b) (числа с доски не стираются). Можно ли через несколько таких операций получить на доске число 1996?
7. На стороне ОА угла АОВ взяты точки А1, А2 и А3 так, что А1А2=2А2А3. На стороне ОВ того же угла взяты точки В1, В2 и В3 так, что В1В2=2В2В3. Пусть С1, С2, С3 - середины отрезков А1В1, А2В2, А3В3 соответственно. Докажите, что С1С2=2С2С3.
8. Петя написал наименьшее натуральное число вида aa...a, которое кратно 1996. Чему равно а ?
9. Сколько раз в течение суток часовая и минутная стрелки правильно идущих часов образуют угол в 30 градусов?
10. Докажите, что любой треугольник можно разрезать ровно на пять равнобедренных треугольников.
1. На плоскости нарисовано 1997 прямых. Докажите, что на ней можно так нарисовать оси координат, что произведение угловых коэффициентов данных прямых в этой системе координат будет положительным. В равнобедренном треугольнике ABC углы B и C равны по 72o. Проведена биссектриса BD. Докажите, что на прямой BC найдется такая точка E, что AD=DE=EC.
2. Числа a и b больше 1. Докажите, что a+b+(1/(ab)) < (1/a)+(1/b)+ab .
3. На доске выписаны числа 1, 2, ..., 1000. На каждом этапе одновременно стираются все числа, имеющие среди нестертых чисел ровно один делитель (например, на первом этапе стирается только число 1). Какие числа будут стерты на последнем этапе?
4. Докажите, что произвольный выпуклый многоугольник можно разбить на конечное число вписанных четырехугольников.
5. Два игрока по очереди красят клетки доски 3*3. Вначале все клетки белые. Первый игрок красит клетки в красный, а второй - в синий цвет. За один ход каждый может закрасить не более трех клеток, из которых не более одной небелой. Первый игрок хочет получить красный квадрат 2*2. Может ли второй ему помешать?
6. На кружок пришло 58 школьников. Оказалось, что из любых 10 из них хотя бы трое учатся в одном классе. Докажите, что хотя бы 15 школьников учатся в одном классе.
7. На доске написаны 3 числа (сначала это были числа 5, 11, 17). Разрешается написать на доске сумму двух из них минус третье, после чего стереть то число|, которое вычиталось. Через некоторое время на доске оказались три числа, наименьшее из которых равно 1997. Какие были два остальных?
8. Докажите, что произвольное натуральное число можно представить в виде суммы нескольких слагаемых вида 2n-1, так, чтобы, если вычеркнуть наименьшее слагаемое, то все оставшиеся будут различными.
9. На занятие кружка пришло 58 учеников. Оказалось, что среди любых 10 из них найдутся хотя бы трое одноклассников. Докажите, что хотя бы 15 из этих учеников - одноклассники.
10. Углы при вершинах B и C треугольника ABC равны 70o, BD - биссектриса угла B. Существует ли на прямой BC такая точка E, что AD=DE=EC ?
1. Можно ли так расставить шахматных коней на бесконечной клетчатой доске, чтобы любые две различные клетки в любом квадрате 3*3 находились под боем разного числа коней?
2. Шесть шахматистов сыграли каждый с каждым по одному разу. Мог ли каждый из них набрать столько же очков белыми, сколько черными? (Новая задача, С.И.Токарев, Иваново)
3. Двое играют в следующую игру. Вначале у каждого из них имеется по 100 однокопеечных, по 80 двухкопеечных, по 60 трехкопеечных и по 40 пятикопеечных монет. Игрок, чья очередь делать ход, выбирает одну из своих монет и передает ее сопернику. Если соперник может разменять эту монету на более мелкие, он обязан сделать это, после чего сам делает очередной ход. Если же соперник не может разменять эту монету, он все равно оставляет ее себе, но очередность хода при этом не изменяется. Начинающий игрок выигрывает, если после очередного хода у него не останется ни одной монеты. Сможет ли второй игрок ему помешать?
4. Найдите все такие тройки простых чисел p, q, r, для которых p+q+r+pq+qr+pr+pqr = 19961995.
5. Даны четыре утверждения:
"2x + y + z - простое число",
"x + 2y + z - простое число",
"x + y + 2z - простое число",
"x, y и z - натуральные числа".
Докажите, что по крайней мере одно из этих утверждений неверно.
6. В выпуклом шестиугольнике площади S соединены середины соседних сторон. Докажите, что площадь получившегося шестиугольника больше S/2.
7. Известно, что три из шести чисел a, b, c, d, e, f равны 1, а остальные три равны 0. Разрешается написать список из четырех вопросов типа: "Чему равна сумма таких-то чисел?" (список может содержать любой набор вопросов, вопрос может содержать любой набор неповторяющихся слагаемых). Можно ли составить этот список так, чтобы, получив ответы на все входящие в него вопосы, однозначно определить все числа?
8. С конечной последовательностью нулей и единиц разрешается производить следующие операции: заменять 01 на 100 или на 110. Может ли для некоторой начальной последовательности процесс замен продолжаться бесконечно?
9. Два кота украли цепочку (незамкнутую) из 100 свиных и 200 говяжьих сосисок. Найдите наименьшее количество разрезов, которое достаточно сделать для произвольного расположения сосисок, чтобы можно было поделить сосиски между котами поровну - по 50 свиных и по 100 говяжьих.
10. Каждая клетка таблицы 100*100 , кроме некоторых двух, расположенных в одной строке, покрашена в один из 100 цветов, при этом в каждой строке и в каждом столбце нет двух клеток одного цвета. Всегда ли удастся покрасить оставшиеся две клетки в какие-то из этих 100 цветов, чтобы указанное свойство сохранилось?
1. Найдите все тройки натуральных чисел, таких, что сумма чисел каждой тройки равна 1996, а сумма любых двух из них кратна третьему.
2. Можно ли с помощью песочных часов на 69 минут и 91 минуту отмерить ровно 1996 минут подряд (песок сыпется равномерно, вначале в каждых часах одна из половинок должна быть пустой)?
3. Трое ребят играли в слова. Каждый составил по 10 слов. Если слово есть у всех, оно вычеркивается, если ровно у двоих - оба получают по одному очку, за остальные свои слова каждый получает по три очка. В итоге все трое набрали разное количество очков, меньше всех - 19 очков - набрал Кузя. По сколько очков набрали остальные игроки?
4. Катеты AB и AC равнобедренного прямоугольного треугольника ABC равны 1. Окружность, вписанная в угол BAC, делит гипотенузу AC на 3 равные части. Найдите радиус окружности.
5. Можно ли выложить бесконечный лист клетчатой бумаги
неперекрывающимися фигурками вида (фигурки можно поворачивать)?
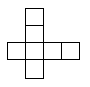
6. Какое наименьшее число участников может быть в математическом кружке, если известно, что девочки в нем составляют меньше 44%, но больше 43% ?
7. Можно ли так расставить шахматных коней на бесконечной клетчатой доске, чтобы любые две соседние клетки находились под боем различного числа коней? (Соседними называются клетки, имеющие одну или две общих вершины.)
8. Из пункта A в пункт B выехал с постоянной скоростью велосипедист. Одновременно с ним из пункта B в пункт A вышли с постоянными скоростями два пешехода, причем скорость первого больше скорости второго пешехода в полтора раза. Велосипедист встретился с первым пешеходом через 5 часов, а со вторым - еще через 50 минут. Найдите отношения скоростей велосипедиста и пешеходов.
9. На доске выписаны все целые числа от 1 до 14, каждое - по одному разу. Двое играющих по очереди стирают по одному числу до тех пор, пока не останется ровно два числа. Если их сумма - точный квадрат, то выигрывает второй, иначе - первый. Кто выигрывает при правильной игре?
10. Можно ли из бесконечной клетчатой плоскости удалить такие два непересекающихся "луча" ("лучом" называются клетки одной строки или одного столбца, идущие подряд, начиная с некоторой клетки плоскости), чтобы, начав с некоторой неудаленной клетки, обойти всю оставшуюся плоскость? Разрешается переходить из любой клетки плоскости на любую соседнюю по горизонтали или вертикали неудаленную клетку, которая не была пройдена ранее.
1. Семиклассник разрезал бумажный квадрат на прямоугольники периметра 7 см, а восьмиклассник - точно такой же квадрат на прямоугольники периметра 8 см. Может ли у восьмиклассника получиться больше прямоугольников?
2. На белой доске размером 4*n двое по очереди красят по одной клетке, причем никакие две закрашенные клетки не должны граничить между собой по вертикали или горизонтали и никакую клетку нельзя красить второй раз. Проигрывает тот, кто не может сделать очередной ход без нарушения правил. Кто выигрывает при правильной игре: тот, кто делает первый ход, или его партнер?
3. С конечной последовательностью нулей и единиц разрешается производить следующую операцию: заменять 01 на 10...0 (число нулей на каждом шаге произвольно). Может ли для некоторой начальной последовательности процесс замен продолжаться бесконечно?
4. При каких натуральных значениях n можно так покрасить конечное число клеток бесконечного клетчатого листа, чтобы каждая покрашенная клетка имела ровно n покрашенных соседей?
5. По окружности произвольным образом расставлены все натуральные числа от 1 до 100 (каждое из них встречается ровно один раз). Докажите, что среди них найдутся шесть расположенных подряд чисел, среди которых не более одного делится нацело на 3.
6. Вначале на доске написаны числа 1, 9, 9, 6, и только они. Разрешается выбрать из написанных на доске чисел три произвольных числа a, b и c и дописать на доску три числа a(b+c), b(c+a) и c(a+b) (числа с доски не стираются). Можно ли через несколько таких операций получить на доске число 1996?
7. Какое наибольшее число слонов можно добавить к шести ладьям, чтобы все эти фигуры можно было расставить на шахматной доске так, чтобы они не били друг друга?
8. На сторонах AB, BC и CA треугольника ABC отмечены соответственно точки A1, B1 и C1 такие: что AA1=2A1B, BB1=B1C, CC1=C1A. Восстановите треугольник ABC, зная только точки A1, B1 и C1.
9. В печатном станке сломалась цифра "3", поэтому в типографии решили нумеровать страницы, используя только числа без "3": 1, 2, 4, ..., 28, 29, 40, 41, 42 и т.д. Какой номер будет иметь 1996-я (в обычной нумерации) страница?
10. Укажите хотя бы один момент времени, отличный от 6:00 и 18:00, когда часовая и минутная стрелки правильно идущих часов направлены в противоположные стороны.
1. Два игрока по очереди красят клетки доски 3*3. Вначале все клетки белые. Первый игрок красит клетки в красный, а второй - в синий цвет. За один ход каждый может закрасить не более трех клеток, из которых не более одной небелой. Первый игрок хочет получить красный квадрат 2*2. Может ли второй ему помешать?
2. Докажите, что произвольный выпуклый многоугольник можно разбить на конечное число четырехугольников, у каждого из которых сумма противоположных углов равна 180o.
3. На автобусной остановке стояли несколько школьников. На первом автобусе уехал каждый десятый из них, на втором - каждый седьмой из оставшихся, а на третьем - каждый пятый из оставшихся, после чего на остановке осталось 111 школьников. Сколько школьников было вначале на остановке?
4. На доске написаны 3 числа (сначала это были числа 5, 11, 17). Разрешается написать на доске сумму двух из них минус третье, после чего стереть то число, которое вычиталось. Через некоторое время на доске оказались три числа, наименьшее из которых равно 1997. Какие были два остальных?
5. На доске выписаны числа 1, 2, ..., 1000. На каждом этапе одновременно стираются все числа, имеющие среди нестертых чисел ровно один делитель (например, на первом этапе стирается только число 1). Какие числа будут стерты на последнем этапе?
6. Новая фигура "заяц" может ходить на одну клетку вверх по любой диагонали или на клетку вниз по вертикали. За какое наименьшее число ходов заяц сможет обойти все поля доски 7*7 и вернуться на исходное поле?
7. Каждая точка плоскости окрашена в один из двух цветов. Докажите, что на этой плоскости найдутся три одноцветные точки, являющиеся вершинами прямоугольного треугольника с гипотенузой 2 см и острым углом 30o.
8. Во время предвыборной кампании каждый из кандидатов на пост президента выступал со своей программой. Среди обещаний, данных кандидатами, было вего пять различных. Оказалось, что наборы обещаний у разных кандидатов различны, однако у любых двух кандидатов совпало по крайней мере по одному обещанию. Какое наибольшее число кандидатов могло участвовать в этой предвыборной кампании?
9. На занятие кружка пришло 58 учеников. Оказалось, что среди любых 10 из них найдутся хотя бы трое одноклассников. Докажите, что хотя бы 15 из этих учеников - одноклассники.
10. Углы при вершинах B и C треугольника ABC равны 72o, BD - биссектриса угла B. Существует ли на прямой BC такая точка E, что AD=DE=EC?
1. Можно ли так расставить шахматных коней на бесконечной клетчатой доске, чтобы любые две различные клетки в любом квадрате 3*3 находились под боем разного числа коней?
2. Шесть шахматистов сыграли каждый с каждым по одному разу. Мог ли каждый из них набрать столько же очков белыми, сколько черными? (Новая задача, С.И.Токарев, Иваново)
3. Двое играют в следующую игру. Вначале у каждого из них имеется по 100 однокопеечных, по 80 двухкопеечных, по 60 трехкопеечных и по 40 пятикопеечных монет. Игрок, чья очередь делать ход, выбирает одну из своих монет и передает ее сопернику. Если соперник может разменять эту монету на более мелкие, он обязан сделать это, после чего сам делает очередной ход. Если же соперник не может разменять эту монету, он все равно оставляет ее себе, но очередность хода при этом не изменяется. Начинающий игрок выигрывает, если после очередного хода у него не останется ни одной монеты. Сможет ли второй игрок ему помешать?
4. Найдите все такие тройки простых чисел p, q, r, для которых p+q+r+pq+qr+pr+pqr=19961995.
5. Даны четыре утверждения:
"2x + y + z - простое число",
"x + 2y + z - простое число",
"x + y + 2z - простое число",
"x, y и z - натуральные числа".
Докажите, что по крайней мере одно из этих утверждений неверно.
6. В выпуклом шестиугольнике площади S соединены середины соседних сторон. Докажите, что площадь получившегося шестиугольника больше S/2.
7. Известно, что три из шести чисел a, b, c, d, e, f равны 1, а остальные три равны 0. Разрешается написать список из четырех вопросов типа: "Чему равна сумма таких-то чисел?" (список может содержать любой набор вопросов, вопрос может содержать любой набор неповторяющихся слагаемых). Можно ли составить этот список так, чтобы, получив ответы на все входящие в него вопосы, однозначно определить все числа?
8. С конечной последовательностью нулей и единиц разрешается производить следующие операции: заменять 01 на 100 или на 110. Может ли для некоторой начальной последовательности процесс замен продолжаться бесконечно?
9. Два кота украли цепочку (незамкнутую) из 100 свиных и 200 говяжьих сосисок. Найдите наименьшее количество разрезов, которое достаточно сделать для произвольного расположения сосисок, чтобы можно было поделить сосиски между котами поровну - по 50 свиных и по 100 говяжьих.
10. Каждая клетка таблицы 100*100, кроме некоторых двух, расположенных в одной строке, покрашена в один из 100 цветов, при этом в каждой строке и в каждом столбце нет двух клеток одного цвета. Всегда ли удастся покрасить оставшиеся две клетки в какие-то из этих 100 цветов, чтобы указанное свойство сохранилось?