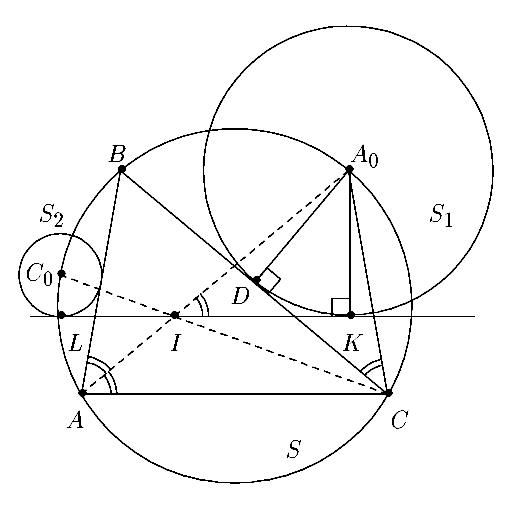
Заключительный этап
1998/99 учебный год
Задачи пятого (финального) этапа XXV Российской олимпиады школьников по математике. Задания подготовлены Методическим Советом Российской математической олимпиады школьников.
Скачать zip-архив этой страницы в месте с рисунками (vmo25h.zip, 65751b)
V тур подготовили:
Н. Агаханов, М. Антонов, А. Белов, С. Берлов, А. Голованов, А. Грабежной,
В. Дольников, С. Злобин, М. Евдокимов, И. Изместьев, Р. Карасёв, Д. Карпов,
П. Кожевников, О. Подлипский, И. Рубанов, Р. Садыков,
В. Сендеров, А. Скопенков, М. Сонкин, Д. Терёшин,
С. Токарев, С. Тухвебер, Г. Челноков.
9.1.(С. Волченков) В числе A цифры идут в возрастающем порядке (слева направо). Чему равна сумма цифр числа 9*A ?
9.2.(Д. Карпов) В стране несколько городов, некоторые пары городов соединены беспосадочными рейсами одной из N авиакомпаний, причем из каждого города есть по одному рейсу каждой из авиакомпаний. Известно, что из любого города можно долететь до любого другого (возможно, с пересадками). Из-за финансового кризиса был закрыт N-1 рейс, но ни в одной из авиакомпаний не закрыли более одного рейса. Докажите, что по-прежнему из любого города можно долететь до любого другого.
9.3.(М. Сонкин) Треугольник ABC вписан в окружность S . Пусть A0 - середина дуги BC окружности S , не содержащей A ; C0 - середина дуги AB , не содержащей C . Окружность S1 с центром A0 касается BC , окружность S2 с центром C0 касается AB . Докажите, что центр I вписанной в треугольник ABC окружности лежит на одной из общих внешних касательных к окружностям S1 и S2 .
9.4.(С. Берлов) Числа от 1 до 1000000 покрашены в два цвета - черный и белый. За ход разрешается выбрать любое число от 1 до 1000000 и перекрасить его и все числа, не взаимно простые с ним, в противоположный цвет. Вначале все числа были черными. Можно ли за несколько ходов добиться того, что все числа станут белыми?
10.1.(Ф. Бахарев) На столе стоят три пустых банки из-под меда. Винни-Пух, Кролик и Пятачок по очереди кладут по одному ореху в одну из банок. Их порядковые номера до начала игры определяются жребием. При этом Винни может добавлять орех только в первую или вторую банку, Кролик - только во вторую или третью, а Пятачок - в первую или третью. Тот, после чьего хода в какой-нибудь банке оказалось ровно 1999 орехов, проигрывает. Докажите, что Винни-Пух и Пятачок могут, договорившись, играть так, чтобы Кролик проиграл.
10.2.(С. Волченков) Найдите все бесконечные ограниченные последовательности натуральных чисел a1, a2, a3, ..., для всех членов которых, начиная с третьего, выполнено an=(an-1+an-2)/(НОД(an-1,an-2)).
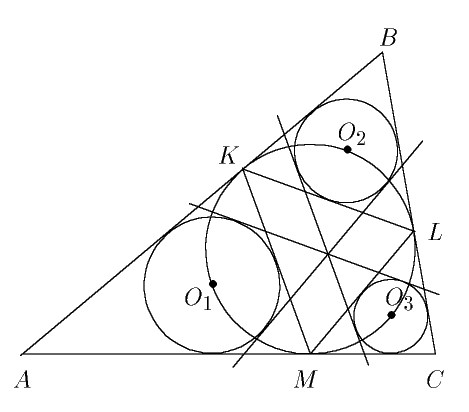
10.3.(М. Сонкин) Пусть окружность, вписанная в треугольник ABC, касается его сторон AB, BC и AC в точках K, L и M соответственно. К окружностям, вписанным в треугольники BKL, CLM и AKM, проведены попарно общие внешние касательные, отличные от сторон треугольника ABC. Докажите, что эти касательные пересекаются в одной точке.
10.4.(С. Токарев) В квадрате n*n клеток бесконечной шахматной доски расположены n2 фишек, по одной фишке в каждой клетке. Ходом называется перепрыгивание любой фишкой через соседнюю по стороне фишку, непосредственно за которой следует свободная клетка. При этом фишка, через которую перепрыгнули, с доски снимается. Докажите, что позиция, в которой дальнейшие ходы невозможны, возникнет не ранее, чем через [n2/3] ходов.
11.1.(О. Подлипский) Существуют ли 19 попарно различных натуральных чисел с одинаковой суммой цифр таких, что их сумма равна 1999?
11.2.(С. Берлов) Во всех рациональных точках вещественной прямой расставлены целые числа. Докажите, что найдётся такой отрезок, что сумма чисел на его концах не превосходит удвоенного числа в его середине.
11.3.(М. Сонкин) Окружность, вписанная в четырёхугольник ABCD, касается его сторон DA, AB, BC, CD в точках K, L, M, N соответственно. Пусть S1, S2, S3, S4 - соответственно окружности, вписанные в треугольники AKL, BLM, CMN, DNK. К окружностям S1 и S2, S2 и S3, S3 и S4, S4 и S1 проведены общие внешние касательные, отличные от сторон четырёхугольника ABCD. Докажите, что четырёхугольник, образованный этими четырьмя касательными - ромб.
11.4.(С. Токарев) В квадрате n*n клеток бесконечной шахматной доски расположены n2 фишек, по одной фишке в каждой клетке. Ходом называется перепрыгивание любой фишкой через фишку, непосредственно за которой следует свободная клетка. При этом фишка, через которую перепрыгнули, с доски снимается. Докажите, что позиция, в которой дальнейшие ходы невозможны, возникнет не ранее, чем через [n2/3] ходов.
9.1. Ответ. 9. Заметим, что 9A=10A-A . При вычитании этих чисел столбиком ни в одном разряде, кроме младшего, не приходится занимать единицу из следующего разряда. Таким образом, сумма цифр разности равна разности суммы цифр чисел 10A и A (которые равны) плюс 9.
9.2. Рассмотрим некоторый путь, соединяющий некоторые два города, возможно включающий в себя некоторые закрытые после кризиса рейсы. Покажем, что в этом пути любой закрытый рейс можно заменить последовательностью незакрытых. Пронумеруем авиакомпании числами от 1 до N. В одной из авиакомпаний сохранились все рейсы: предположим, что в первой. Тогда в любой другой авиакомпании закрыли по одному рейсу. Рассмотрим только рейсы первой и второй авиакомпаний: из каждого города выходит по одному рейсу этих авиакомпаний. Следовательно, все города разбиваются на циклы. В одном из этих циклов закрыли один рейс. Очевидно, можно пролететь остальными рейсами этого цикла, следовательно, мы можем "обойти" любой закрытый рейс. Отметим, что мы при этом не используем рейсы других авиакомпаний, следовательно, аналогично можно обойтись без остальных закрытых рейсов.
9.3. Из точки I проведём касательную IK к окружности S1 так, чтобы луч IK пересекал меньшую дугу A0C (см. рис. ). Аналогичным образом проведём касательную IL к окружности S2 .
Биссектриса AI угла BAC делит дугу BC на 2 равных дуги. Поэтому точки A, I, A0 лежат на одной прямой. Аналогично, на одной прямой лежат точки C, I и C0.
Из равенств
/ICA0 = /C0CA0 = (1/2) дуга C0BA0 = (1/2)(дуга C0B + дуга BA0) ,
/A0IC = (1/2)(дуга AC0 + дуга A0C)= (1/2)(дуга C0B + дуга BA0)
следует, что /A0IC= /ICA0 и A0I= A0C .Далее, пусть D - середина отрезка BC , тогда S1 касается BC в точке D .
В прямоугольных треугольнике A0KI и треугольнике
A0DC катеты A0K и
A0D равны и
A0I=A0C по доказанному выше.
Следовательно, треугольник A0KI = треугольнику
A0DC. Отсюда
/A0IK=/A0CD=
/A0CB. Но
/A0CB=/A0AB ,
(теорема о вписанном угле) и
/A0AB=/A0AC .
Значит,
/A0IK=/A0AC ,
следовательно прямая IK параллельна AC. Аналогично,
IL||AC, следовательно L, I,
K лежат на одной прямой, параллельной AC.
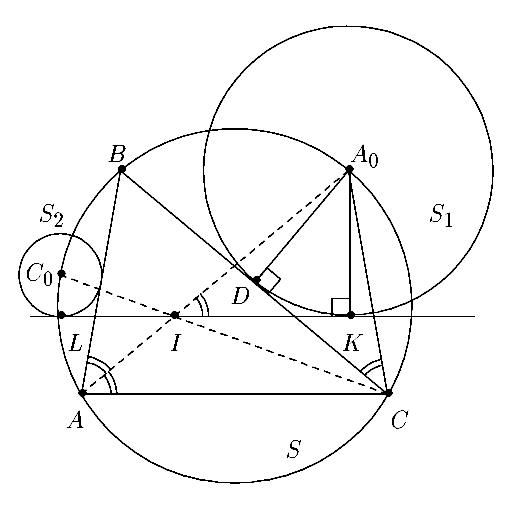
9.4. Ответ. Можно.
Лемма. Пусть дан набор простых чисел p1,... ,pn . Тогда можно за несколько перекрашиваний добиться того, что поменяют цвет те и только те числа, которые делятся на все простые числа набора.
Доказательство. (по формуле включения-исключения): для каждого непустого поднабора чисел перекрасим числа, не взаимно простые с произведением всех чисел этого поднабора. Число, делящееся на все числа набора, перекрашивалось при каждом таком перекрашивании, всего перекрашиваний было 2n-1, следовательно, числа, делящиеся на все числа набора перекрашены. Пусть некоторое число k не делится хотя бы на одно из чисел набора, например, на p1. Тогда оно не перекрашивалось, когда мы перекрашивали числа, не взаимно простые с p1. Остальные непустые поднаборы чисел можно разбить на пары следующим образом: поднабору, не содержащему p1, в пару ставится поднабор, полученный из него добавлением p1. При этом число k перекрашивается или при обоих перекрашиваниях пары, или ни при одном. Поэтому число k не будет перекрашено.
Лемма доказана.
Первое решение. Для каждого набора простых чисел, произведение которых не больше 1000000 , перекрасим числа, делящиеся на все эти простые числа. По лемме такая операция возможна. Докажем, что любое число k при этом будет перекрашено. Пусть k имеет m различных простых делителей, тогда оно перекрашивалось при 2l-1 операции, то есть нечетное число раз.
Второе решение. Назовем два числа эквивалентными, если у них совпадают наборы простых делителей. Заметим, что при наших операциях классы эквивалентности перекрашиваются целиком. Будем говорить, что один класс больше другого, если если все простые делители второго класса являются делителями первого. Из леммы следует, что мы можем перекрасить любой класс, перекрасив вместе с ним только большие классы.
Сначала перекрасим минимальные классы (класс называется минимальным, если он не больше никакого другого класса). Исключим их из рассмотрения. Среди оставшихся некоторые классы станут после такого исключения минимальными. При необходимости перекрасим их и тоже исключим. И так далее.
Поскольку классов конечное число, процесс закончится.
10.1. Пусть Винни и Пятачок вначале кладут свои орехи во вторую и третью банки, несмотря на ходы Кролика, до тех пор, пока в одной из банок не станет 1998 орехов. После этого тот, кто должен класть орехи в эту банку (пусть, например, это Винни) начинает класть их в I. При этом он уже положил во II банку не менее 999 орехов, значит, в III орехов тоже не менее 999 (туда их клал Пятачок). После этого Пятачок продолжает класть в III банку орехи, пока там не станет 1998 - это произойдёт не более, чем через 500 ходов, так как в III банку также приходится класть орехи Кролику, чтобы не проиграть. После этого Пятачок также может класть орехи в I банку, так как там не более 500 орехов, положенных Винни, а Кролик вынужден будет положить орех во II или III, где их уже по 1998.
10.2. Ответ. a1=a2=...=2 . Пусть для каких-то двух членов последовательности ak и ak+1 их НОД равен 1. Тогда НОД(ak, ak+1)= НОД(ak+ak+1, ak+1)= НОД(ak+2, ak+1) , т. е. для всех последующих членов последовательности НОД тоже будет равен 1. При этом, начиная с k-го члена, последовательность превращается в последовательность an= an-1+an-2 , которая неограниченно возрастает.
Итак, НОД всегда должен быть не меньше 2. Если какие-то члены последовательности ak и ak+1 не равны друг другу, то
ak+2 < max(ak, ak+1) и ak+1 не равно ak+2 .
Аналогично, ak+3 < max(ak+1, ak+2) < max(ak, ak+1) .
Мы получили, что максимальное число в парах идущих подряд членов последовательности монотонно убывает, т. е. когда-то станет равным 1, и тогда НОД у каких-то членов тоже станет равен 1, что не должно случиться.
Итак, все члены последовательности должны равняться друг другу и их НОД=2 , т. е. an=2 .
10.3.
Пусть K, L, M - точки касания вписанной окружности, со
сторонами AB, BC, AC соответственно,
O1, O2, O3 -
центры малых окружностей (см. рис. ), так как
/KO1M=90o+(/A/2), а
/KLM=90o-(/A/2), то
/KO1M+/KLM=180o,
и O1 лежит на вписанной в треугольник ABC окружности.
Аналогично O2 и O3 лежат на этой
окружности и являются серединами дуг KL и LM. Используя
результат задачи 9.3 заключаем, что построенные касательные проходят через
центр окружности, вписанной в треугольник KLM, что и требовалось
доказать.
10.4. Будем различать два типа ходов - внутренние и внешние, в зависимости от того, куда ставится фишка, делающая ход: внутрь исходного квадрата n*n клеток, или вне его.
Пусть получена позиция, где дальнейшие ходы невозможны, причём сделано k внутренних ходов и l внешних.
Ясно, что никакие две фишки не находятся в соседних клетках, а в исходном квадрате n*n не менее, чем [n2/2] клеток пусты. Так как каждый внутренний ход увеличивал количество пустых клеток не более, чем на 1, а каждый внешний - не более, чем на 2, то имеем неравенство
k+2l > [n2/2] . (1)
Предположив теперь, что n чётно, разобьём исходный квадрат на n2/4 четырёхклеточных квадратиков и заметим, что на каждый квадратик пришлось не менее двух ходов, в которых участвовали (делали ход или снимались с доски) фишки, стоявшие в клетках этого квадратика. Поскольку в каждом внутреннем ходе участвовали фишки не более, чем двух квадратиков, а в каждом внешнем - не более, чем одного, то
2k+l > 2n2/4 . (2)
Из неравенств (1) и (2) получаем k+l > n2/3 > [n2/3], т. е. утверждение задачи в этом случае верно.
Легко видеть, что оно верно также при n=1 и при n=3 .
В случае n=2m+1 , где m>1 , в "кресте", образованном третьей сверху горизонталью и третьей слева вертикалью, выделим 2m "доминошек", а остальную часть исходного квадрата разобьём на m2 четырёхклеточных квадратиков. В каждом внутреннем ходе участвовать могли фишки, принадлежащие не более, чем двум из m2+2m рассматриваемых фигур, а в каждом внешнем - не более, чем одной. Имеем неравенство
2k+l > 2m2+2m , (3)
поскольку фишки каждого из квадратиков участвовали не менее, чем в двух ходах, а фишки каждой "доминошки" - по крайней мере в одном.Из (1) и (3) следует, что 3(k+l)>4m2+4m= n2-1 . Если здесь n2=0 (mod 3) , то, очевидно, 3(k+l)>n2 и k+l>n2/3=[n2/3] , в противном случае n2=1(mod 3) и k+l>(n2-1)/3= [n2/3] . Тем самым утверждение задачи полностью доказано.
11.1. Ответ. Нет. Пусть сумма цифр каждого из чисел равна S=9k+n , n=0, 1, ..., 8 . Тогда все эти числа имеют остаток n при делении на 9, и имеет место сравнение 19n=18n+n = 1999 (mod 9) , откуда n = 1 (mod 9) , т. е n=1 .
1) Пусть k=0 , т. е. S=1 . Рассмотрим 5 наименьших натуральных чисел с суммой цифр, равной 1. Это числа 1, 10, 100, 1000 и 10000. Но даже их сумма больше 1999.
2) Пусть k=1 , т. е. S=10 . Рассмотрим 19 наименьших натуральных чисел чисел с суммой цифр, равной 10. Это числа 19, 28, 37, 46, 55, 64, 73, 82, 91, 109, 118, 127, 136, 145, 154, 163, 172, 181, 190. Их сумма равна 1990<1999 . Следующее натуральное число с суммой цифр, равной 10, есть 208, что по крайней мере на 18 больше любого из первых 19 чисел, и значит, сумма будет не менее 1990+18=2008>1999 .
3) Пусть k>2 , т. е. S>19 . Но наименьшее число с суммой цифр не меньше 19 есть 199, а сумма любых 19 таких чисел будет заведомо больше 1999.
Таким образом, мы получили, что 19 чисел, удовлетворяющих условию, не существует.
11.2.
Предположим противное, т. е. существует такая расстановка целых чисел, что
для любого отрезка AB с серединой C выполняется неравенство
c<(a+b)/2 , где a, b, c -
соответственно числа, стоящие в точках A, B и C .
Пусть A, B, C, An,
Bn, n=1, 2, ... - соответственно точки
-1, 1, 0, -1/2n, 1/2n числовой прямой,
a, b, c, an,
bn - целые числа, записанные в этих точках.
Тогда, по предположению,
c<(a+b)/2 ,
a1<(a+c)/2 ,
a2<(a1+c)/2 и т.д.
Отсюда следует, что
max(a, c)>max(a1, a2),
так как a1<(a+c)/2<
(max(a, c)+max(a, c))/2=max(a, c) ,
a2<(a1+c)/2<(max(a, c)+c)/2<max(a, c) .
Аналогично,
max(a1, a2)>max(a3, a4)>max(a5, a6)>... и
max(b, c)>max(b1,b2)>max(b3, b4)>... .
Таким образом, a2m < max(a, c)-m,
b2m < max(b, c)-m и, значит,
при некотором m будет выполнено неравенство
a2m+b2m < 2c .
Противоречие, так как число c записано в середине отрезка
A2mB2m .
11.3. Введём обозначения (см. рис. ). Как было показано в решении задачи 9.3, RQ||KM||EF , RE||LN||QF . Значит, образовавшийся четырёхугольник - параллелограмм. Используя то, что касательные к окружности, проведённые из одной точки, равны и AB+CD=AD+BC , получаем RQ+EF=RE+QF , так как (RQ+EF)-(RE+QF)= (a12+a34)- (a23+a41) , где aij - длина общей внешней касательной к окружностям Si и Sj .
Значит, RQFE - ромб.

11.4. См. решение задачи 10.4.
9.5.(М. Антонов)
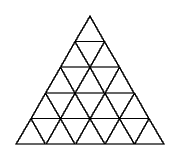
Правильный треугольник разбит на правильные треугольники со стороной 1 линиями,
параллельными его сторонам и делящими каждую сторону на n частей (на
рисунке n=5 ).
Какое наибольшее число отрезков длины 1 с концами в вершинах этих треугольников можно отметить так, чтобы не нашлось треугольника, все стороны которого состоят из отмеченных отрезков?
9.6.(А. Храбров) Докажите, что при любом натуральном n справедливо неравенство
| n2 | |
| S | {k1/2} < (n2 - 1)/2 |
| k=1 |
9.7.(С. Берлов) Окружность, проходящая через вершины A и B треугольника ABC, пересекает сторону BC в точке D. Окружность, проходящая через вершины B и C, пересекает сторону AB в точке E и первую окружность вторично в точке F. Оказалось, что точки A, E, D, C лежат на окружности с центром O. Докажите, что угол BFO - прямой.
9.8.(Д. Карпов) В микросхеме 2000 контактов, первоначально любые два контакта соединены отдельным проводом. Хулиганы Вася и Петя по очереди перерезают провода, причем Вася (он начинает) за ход режет один провод, а Петя - либо один, либо три провода. Хулиган, отрезающий последний провод от какого-либо контакта, проигрывает. Кто из них выигрывает при правильной игре?
10.5.(А. Голованов) Сумма цифр в десятичной записи натурального числа n равна 100, а сумма цифр числа 44n равна 800. Чему равна сумма цифр числа 3n?
10.6.(С. Берлов) В треугольнике ABC окружность, проходящая через вершины A и B, касается прямой BC, а окружность, проходящая через вершины B и C, касается прямой AB и пересекает первую окружность в точке K, K != B. Пусть O - центр описанной окружности треугольника ABC. Докажите, что угол BKO - прямой.
10.7.(С. Злобин) Для некоторых положительных чисел x и y выполняется неравенство x2+y3> x3+y4. Докажите, что x3+y3<2 .
10.8.(В. Дольников) В некоторой группе из 12 человек среди каждых 9 найдутся 5 попарно знакомых. Докажите, что в этой группе найдутся 6 попарно знакомых.
11.5.(С. Берлов) Четыре натуральных числа таковы, что квадрат суммы любых двух из них делится на произведение двух оставшихся. Докажите, что по крайней мере три из этих чисел равны между собой.
11.6.(В. Дольников) Докажите, что три выпуклых многоугольника на плоскости нельзя пересечь одной прямой тогда и только тогда, когда каждый многоугольник можно отделить от двух других прямой (т. е. существует прямая такая, что этот многоугольник и два остальных лежат по её разные стороны).
11.7.(Д. Терёшин) Через вершину A тетраэдра ABCD проведена плоскость, касательная к описанной около него сфере. Докажите, что линии пересечения этой плоскости с плоскостями граней ABC, ACD и ABD образуют шесть равных углов тогда и только тогда, когда AB*CD=AC*BD=AD*BC .
11.8.(Д.Карпов) В микросхеме 2000 контактов, первоначально любые два контакта соединены отдельным проводом. Хулиганы Вася и Петя по очереди перерезают провода, причем Вася (он начинает) за ход режет один провод, а Петя - либо два, либо три провода. Хулиган, отрезающий последний провод от какого-либо контакта, проигрывает. Кто из них выигрывает при правильной игре?
9.5. Ответ. n(n+1) . Общее количество отрезков длины 1 равно 3*n(n+1)/2 . Все отрезки, параллельные двум сторонам большого треугольника, не образуют треугольников, так как любой треугольник состоит из отрезков, параллельных всем трём сторонам. Следовательно, (2/3)(3*n(n+1)/2)=n(n+1) отрезков длины 1 отметить можно.
Докажем, что большее количество отрезков отметить нельзя.
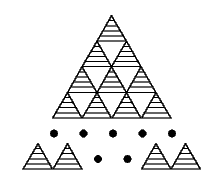
Заштрихуем треугольники со стороной 1, как показано на рис. Треугольники содержат все отрезки длины 1, причём каждый отрезок принадлежит ровно одному треугольнику. Для того, чтобы не образовался ни один из заштрихованных треугольников, в каждом из них можно отметить не более двух отрезков. Значит, количество выделенных отрезков не превышает 2/3 от их общего числа.
9.6. При n=1 неравенство обращается в равенство 0=0 . При n>1 докажем, что сумма дробных частей на каждом промежутке между двумя последовательными квадратами удовлетворяет неравенству
| m2+2m | |
| S | {k1/2} < (2m+1)/2 |
| k=m2 |
Нетрудно проверить (например, возведением в квадрат), что
(m2+a)1/2+(m2+2m-a)1/2 < 2m+1 при 0 < a < m .
Следовательно,{(m2+a)1/2}+{(m2+2m-a)1/2} < 1. (2)
Просуммировав эти неравенства при a=0, 1, ..., m-1 и неравенство {(m2+m)1/2}<1/2 (получаемое делением на 2 обеих частей (2) при a=m ), приходим к неравенству (1).Суммируя неравенство (1) по всем m от 1 до n-1 , получаем:
| n2-1 | |
| S | {k1/2} < (n2-1)/2 . |
| k=12 |
Остаётся заметить, что {(n2)1/2}=0 .
9.7.
Заметим, что /BCF=180o-/BEF=/AEF ,
аналогично /EAF=/FDC , значит треугольник AEF
подобен треугольнику DCF . Пусть K и L - середины
отрезков AE и CD соответственно. Тогда
/AKF=/FLB как углы между медианой и основанием в
подобных треугольниках, поэтому точки B, K, F, L
лежат на одной окружности. Но, так как серединные перпендикуляры к отрезкам
AE и CD пересекаются в точке O, то точки K и
L лежат на окружности с диаметром BO . Но тогда и точка
F лежит на этой окружности, и /BFO - прямой.

9.8. Докажем, что выигрывает Петя. Мысленно разобьем контакты на четыре одинаковых группы A, B, C и D. В каждой группе пронумеруем контакты числами от 1 до 500. Петя будет отвечать на любой ход Васи так, чтобы для каждого номера k от контактов Ak, Bk, Ck и Dk отходило поровну проводов. До начала игры это условие, очевидно, выполняется. Именно благодаря этому условию у Пети всегда будет возможность ответить на ход Васи.
Теперь подробнее опишем Петину стратегию. Если Вася перерезает провод между контактами одной группы, например, провод AiAj, то Петя перережет провода BjBj, CiCj и DjDj. Если Вася перерезает провод между проводами из разных групп и с разными номерами, например, провод AiBj, то Петя в ответ перережет провода AjBi, CiDj и CjDi. Если же Вася перерезал провод между контактами из разных групп с одинаковыми номерами, например, провод AkBk, то Петя перережет провод CkDk. Заметим, что из описанной стратегии Пети следует, что провода, которые он собирается резать, не будут отрезаны до его хода.
Такие ходы Петя может сделать, так как из возможности отрезать один провод от некоторого контакта следует возможность отрезать по одному проводу от контактов с таким же номером. Отметим, что каждый раз после хода Пети от контактов Ak, Bk, Ck и Dk отходит поровну проводов. Значит, Петя всегда сможет сделать ход, и, так как количество проводов конечно, проиграет Вася.
10.5. Заметим, что 44n есть сумма 4 экземпляров числа n и 4 экземпляров числа 10n. Если складывать эти числа поразрядно, то в каждом разряде окажется сумма учетверённой цифры из этого же разряда числа n и учетверённой цифры из следующего разряда. Если при этом не происходит никаких переносов, то каждая цифра числа n складывается 8 раз, и сумма цифр во всех разрядах оказывается равной 800. При переносах же сумма цифр, очевидно, уменьшается (так как из одного разряда вычитается 10, а к другому прибавляется только 1). Поэтому в ситуации условия задачи переносов не происходит. Это означает, в частности, что любая цифра числа n не превосходит 2. Тогда при умножении n на 3 просто умножается на 3 каждая его цифра, а, значит, и сумма цифр. Поэтому сумма цифр числа 3n равна 300.
10.6. Задача является частным случаем задачи 9.7, когда точки E и D совпадают с точкой B.
10.7. Вначале докажем, что
x+y2 > x2+y3. (1)
Допустим противное: x+y2<x2+y3, тогда, складывая это неравенство с неравенством x3+y4<x2+y3, получим (x+x3)+(y2+y4)<2x2+2y3, что противоречит неравенствамx+x3>2x2 и y2+y4>2y3.
Из (1) получаемx+y2>x2+y3>x3+y4 , откуда 2x+2y2>x2+y3+x3+y4 .
Замечая, что (1+x2)+(1+y4)>2x+2y2>x2+y3+x3+y4 , получаем неравенство 2+x2+y4>x2+y3+x4+y4 , равносильное требуемому.10.8. Возьмём граф на 12 вершинах, которые соответствуют людям, две его вершины соединены, если люди незнакомы.
Если в этом графе нет циклов нечётной длины, то его можно разбить на две части, в каждой из которых вершины не будут соединены, и поэтому найдутся 6 попарно знакомых.
Предположим теперь, что в графе есть циклы нечётной длины. Рассмотрим нечётный цикл минимальной длины. Пусть его длина равна:
а) 3. Тогда если среди 9 человек, не входящих в этот цикл, есть два незнакомых, то среди оставшихся 7 человек из каждых 4 найдутся три знакомых. Таким образом в подграфе на 7 вершинах каждые два ребра имеют общую вершину. Третье ребро обязано проходить через эту вершину. Иначе среди 4 человек не найдутся трёх знакомых. Поэтому все рёбра имеют общую вершину, и удаляя эту вершину, мы получаем 6 попарно знакомых.
б) 5. Тогда, как и выше, среди оставшихся 7 из каждых 4 найдутся 3 знакомых и среди этих 7 найдутся 6 знакомых.
в) 7. Тогда среди 5 человек, не входящих в этот цикл, все попарно знакомы.
Если есть человек из цикла, знакомый со всеми этими 5, то всё доказано. В
противном случае, каждый из цикла не знаком с кем-то из оставшихся. Так как
7>5, то найдётся человек A из оставшихся, не знакомый с двумя из
цикла B, C . Из того, что мы взяли цикл минимальной длины,
следует, что эти два незнакомых из цикла должны быть знакомы через одного
D. Но тогда D знаком со всеми из пяти оставшихся, потому что
удаляя из цикла D и заменяя на A, мы получаем снова цикл длины 7,
а в дополнении к циклу длины 7 все попарно знакомы.
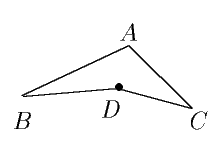
г) Цикла длины 9 не может быть по условию задачи.
д) Цикл длины 11. Тогда, как и выше при рассмотрении циклов длины 7, мы видим, что оставшийся человек может быть незнаком максимум с двумя из цикла. Но тогда в цикле легко найти 5 человек, знакомых между собой и с оставшимся. (Например, взяв идущих через одного по циклу и не знакомых с оставшимся.)
11.5. Набор натуральных чисел, удовлетворяющий условию задачи, условимся называть хорошим.
Пусть существует хороший набор. Ясно, что если (a,b,c,d) - хороший набор, то и (a/k, b/k, c/k, d/k) - тоже хороший набор, где k=НОД(a,b,c,d). Поэтому в дальнейшем считаем, что
НОД(a,b,c,d)=1 (1)
Пусть одно из данных чисел, например a, имеет нечётный простой делитель p. Тогда суммы b+c, c+d, b+d и, следовательно, сами числа b, c и d делятся на p (ибо, например, 2d=(b+d)+(c+d)-(b+c) ), что противоречит условию (1). Значит, числа a, b, c, d - степени двойки. Упорядочив данные числа в порядке возрастания, получим a=2m, b=2n, c=2r, d=2s, где 0=m < n < r < s, r > 1 (иначе m=n=r=0 , значит, a=b=c ).
Тогда число (a+c)2=(1+2r)2 - нечётно и не может делиться на чётное число bd .
11.6. Пусть каждый из многоугольников A, B, C можно отделить от двух других. Докажем, что их нельзя пересечь одной прямой. Предположим противное: X, Y, Z - соответственно точки многоугольников A, B, C, лежащие на одной прямой. Тогда одна из точек, например Y, лежит на прямой между X и Z. Следовательно, B нельзя отделить от A и C, так как в противном случае точку Y, лежащую между двумя другими X и Z, нужно отделить от этих точек одной прямой, что невозможно.
В обратную сторону утверждение можно доказать двумя способами.
1) Рассмотрим треугольники с вершинами XcA,
YcB, ZcC. Пусть из всех таких
треугольников наименьшую высоту имеет треугольник
X0Y0Z0 и эта высота
проведена из вершины Y0. Тогда прямая, перпендикулярная
высоте и проходящая через середину высоты, не пересекает многоугольники
B, A и C, так как, в противном случае, существовал бы
треугольник с меньшей высотой, выходящей из Y0.
2) Рассмотрим две внешние касательные к многоугольникам A и C. Тогда они не могут пересекать B. Если мы сдвинем немного ту, которая лежит ближе к B, в направлении к многоугольнику B, то получим прямую, отделяющую B от A и C.
11.7. Проведём плоскость, параллельную касательной плоскости, пересекающую рёбра AB, AC и AD в точках B1, C1 и D1 соответственно. В плоскости ABC получим конфигурацию, изображённую на рис. Заметим, что /ABC=/CAM (по теореме об угле между касательной и хордой), а /CAM=/AC1B1 (как накрест лежащие при параллельных и секущей), т. е. /ABC=/AC1B1. Следовательно, треугольник AB1C1 подобен треугольнику ACB. Откуда
B1C1/BC= AB1/AC= AC1/AB.
Аналогично,
C1D1/CD = AC1/AD=AD1/AC и
B1D1/BD = AD1/AB = AB1/AD .
Из этих равенств вытекает, что
C1D1/AB*CD=AD1/AB*AC= B1D1/AC*BD=AB1/AD*AC= B1C1/AD*BC
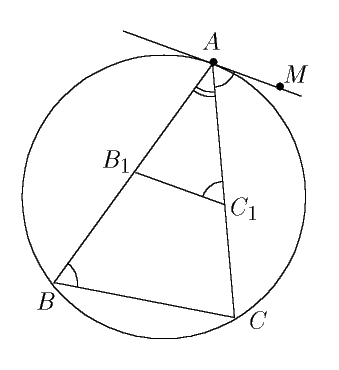
Значит, треугольник A1B1C1 равносторонний тогда и только тогда, когда AB*CD=AC*BD=AD*BC.
Осталось заметить, что углы, образуемые указанными в условии линиями пересечения, соответственно равны углам треугольника A1B1C1 .
11.8. Докажем, что выигрывает Петя. Разобьем контакты на четыре одинаковых группы A, B, C и D. В каждой группе пронумеруем контакты числами от 1 до 500. Мысленно покрасим в черный цвет провода между контактами с разными номерами, и в белый цвет - между контактами с одинаковыми номерами.
Петя будет отвечать на любой ход Васи так, чтобы для каждого номера k от контактов Ak, Bk, Ck и Dk отходило поровну черных проводов, и если у одного из контактов больше нет белых проводов, то их не было бы и у других контактов с таким же номером. До начала игры это условие, очевидно, выполняется. Именно благодаря этому условию у Пети всегда будет возможность ответить на ход Васи.
Теперь подробнее опишем Петину стратегию. Сначала рассмотрим случай, когда Вася режет черный провод. Если Вася перерезает провод между контактами одной группы, например, провод AiAj, то Петя перережет провода BjBj, CiCj и DjDj. Если Вася перерезает провод между проводами из разных групп и с разными номерами, например, провод AiBj, то Петя в ответ перережет провода AjBi, CiDj и CjDi. Такие ходы Петя может сделать, так как из возможности отрезать один провод от некоторого контакта следует возможность отрезать по одному проводу от вершин с таким же номером.
Остается рассмотреть случай, когда Вася перерезал белый провод, то есть, провод между контактами из разных групп, но с одинаковыми номерами. Рассмотрим четыре контакта Ak, Bk, Ck и Dk. Первоначально любые два из них соединены проводом. После того, как Вася перерезал первый из этих проводов, например, провод AkBk, Петя перережет два провода так, чтобы между этих контактов осталось три провода, имеющие один общий конец (например, Петя может перерезать провода BkCk и СkAk, после чего останутся провода AkDk, BkDk и CkDk, что подтверждает возможность такого хода). Если же Вася когда-нибудь перережет один из этих трех проводов, то от одного из контактов Ak, Bk или Ck он отрежет последний провод к контактам с этим же номером k, следовательно, от этого контакта будет отходить провод к контакту с другим номером. Значит, и от трех других контактов с номером k будут отходить провода к контактам с другим номером, следовательно, Петя может перерезать два оставшихся провода между контактами с номером k, что он и сделает.
Отметим, что каждый раз после хода Пети описанное выше условие выполняется. Следовательно, Петя всегда сможет сделать ход, и, так как количество проводов конечно, проиграет Вася.
Общее количество участников по 9 классу - 65 человек.
| баллы | номера задач | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0 | 6 | 37 | 47 | 61 | 2 | 18 | 49 | 38 |
| 1 | 2 | 3 | 4 | 1 | 9 | 14 | 1 | 1 |
| 2 | 0 | 1 | 1 | 0 | 2 | 3 | 1 | 0 |
| 3 | 2 | 1 | 0 | 2 | 1 | 7 | 2 | 3 |
| 4 | 0 | 0 | 1 | 0 | 0 | 4 | 0 | 1 |
| 5 | 2 | 0 | 0 | 0 | 4 | 2 | 1 | 1 |
| 6 | 10 | 2 | 1 | 0 | 3 | 2 | 1 | 1 |
| 7 | 43 | 21 | 11 | 1 | 44 | 15 | 10 | 20 |
Общее количество участников по 10 классу - 51 человек.
| баллы | номера задач | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0 | 1 | 7 | 30 | 45 | 4 | 8 | 37 | 48 |
| 1 | 1 | 1 | 10 | 0 | 0 | 2 | 2 | 2 |
| 2 | 2 | 10 | 0 | 1 | 1 | 0 | 0 | 0 |
| 3 | 4 | 5 | 0 | 0 | 2 | 0 | 0 | 1 |
| 4 | 0 | 3 | 1 | 2 | 0 | 0 | 0 | 0 |
| 5 | 1 | 3 | 0 | 0 | 0 | 0 | 2 | 0 |
| 6 | 2 | 1 | 1 | 1 | 1 | 5 | 1 | 0 |
| 7 | 40 | 21 | 9 | 2 | 43 | 36 | 9 | 0 |
Общее количество участников по 11 классу - 49 человек.
| баллы | номера задач | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 0 | 1 | 2 | 29 | 41 | 17 | 0 | 41 | 33 |
| 1 | 3 | 3 | 3 | 2 | 1 | 1 | 1 | 6 |
| 2 | 1 | 0 | 4 | 3 | 0 | 3 | 0 | 2 |
| 3 | 1 | 4 | 4 | 0 | 2 | 1 | 0 | 0 |
| 4 | 0 | 2 | 1 | 0 | 0 | 5 | 2 | 0 |
| 5 | 3 | 2 | 0 | 1 | 1 | 11 | 0 | 0 |
| 6 | 4 | 6 | 3 | 0 | 1 | 3 | 0 | 0 |
| 7 | 36 | 30 | 5 | 2 | 27 | 25 | 5 | 8 |