Рис. 1.
1. (5 баллов; со второй попытки - 2 балла)
На рисунке 1 даны четыре двусторонних этикетки: А, В, C и D. У каждой этикетки
одна из сторон имеет либо черный, либо белый цвет, а на другой стороне указан
либо четный, либо нечетный номер. Вам надо проверить справедливость утверждения:
"Все этикетки с черной стороной имеют нечетные номера". Какие из этикеток для
этого необходимо перевернуть?

Рис. 1.
2. (5 баллов; со второй попытки - 2 балла)
На рисунке 2 изображена лицевая сторона кирпичной стены, толщиной 20 см.
Какое количество кирпичей, имеющих размеры 5*10*20 см использовано для
постройки стены?
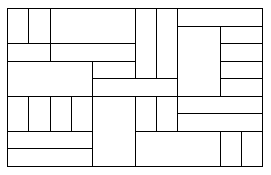
Рис. 2.
3. (5 баллов; со второй попытки - 2 балла)
На карточках записаны цифры: 1; 0; 2. Из этих карточек составлены числа и
записано неверное равенство (см. рис. 3). Покажите, как, переместив только одну
карточку, сделать равенство верным.

Рис. 3.
4. (3 + 5 баллов; со второй попытки - 1 + 3 балла)
В запись выражения
-1,5 - 1,5*0*1,2 - 1,2
вставьте только одни скобки так, чтобы
значение полученного выражения стало:
а) положительным;
б) наименьшим из возможных.
5. (15 баллов; со второй попытки - 7 баллов; с третьей попытки - 3 балла) Математик, получив гонорар за книгу, сказал: "Какое необычное четырехзначное число! Если его разделить на 10, то остаток будет 9, если его разделить на 9, то остаток будет 8, и так далее. В конце концов, когда мы разделим это число на 2, остаток будет равен 1". Каков же был размер его гонорара, если известно, что он не превышал трех тысяч?
6. (10 баллов; со второй попытки - 5 баллов)
На рисунке 4 расположите в кружках все цифры от 1 до 9 так, чтобы для каждого
отрезка, имеющего кружки на концах и посередине, сумма чисел, записанных в этих
трех кружках, равнялась 18.
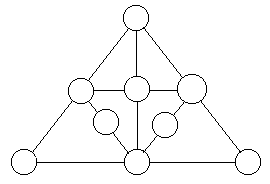
Рис. 4.
7. (10 баллов; со второй попытки - 5 баллов)
Пятачок вышел из своего дома и идет в гости к Пуху через дубовую рощу, собирая
по дороге все желуди (рис. 5). Числа на рисунке обозначают количество желудей,
которое лежит под каждым дубом. Покажите, как шел Пятачок, если известно, что
он собрал ровно 1000 желудей.
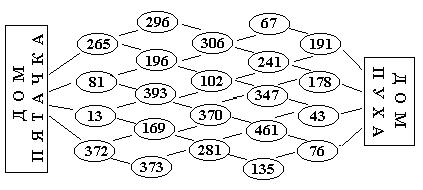
Рис. 5.
8. (15 баллов; со второй попытки - 7 баллов; с третьей попытки - 3 балла)
Кузнечик скачет по клеткам прямоугольника (рис. 6). Число, записанное в клетке,
показывает на сколько клеток он может прыгнуть за один раз по вертикали или
горизонтали. Кузнечик может начать движение с любой из клеток, отмеченных в
левом верхнем углу, и прыгать с одной пронумерованной клетки на другую, не
пересекая собственный путь. Найдите кратчайший (по длине) путь кузнечика до
правого нижнего угла, если первый прыжок был по вертикали.
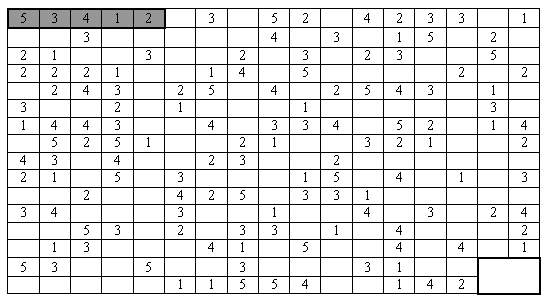
Рис. 6.
9. (10 баллов; со второй попытки - 2 балла)
Переставьте карточки, разложенные в форме квадрата (рис. 7), так, чтобы суммы
записанных на них чисел в каждой горизонтали, каждой вертикали и каждой большой
диагонали стали одинаковыми. Если вы правильно это сделаете, то сможете
прочитать народную мудрость.
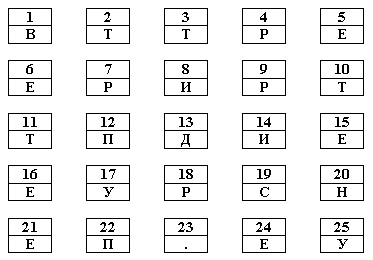
Рис. 7.
10. (10 баллов; со второй попытки - 5 баллов)
Разгадайте кросснамбер (рис. 8):
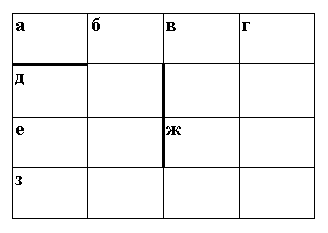
Рис. 8.
По горизонтали:
а) значение произведения 11 и некоторого трехзначного числа;
д) число, которое при делении на 3 дает в остатке 0;
е) число, кратное пяти;
з) год заполнения данного кросснамбера.
По вертикали:
а) число, квадратом которого является число ж) по горизонтали;
б) число, сумма цифр которого делится на 9;
в) число, 3/5 которого равны 2148;
г) число, у которого каждая следующая цифра на единицу меньше предыдущей;
д) куб однозначного числа.
11. (10 + 15 баллов; со второй попытки - 5 + 7 баллов) Японский кроссворд (рис. 9 и 10).
Клетки квадрата закрашены некоторым образом. Числа указывают, сколько подряд
идущих клеток закрашено в данной вертикали или горизонтали. Например, над
некоторым столбцом надписаны числа 6 4 1. Это означает, что в столбце
закрашено три группы клеток, причем первая содержит шесть, вторая - четыре, и
третья - одну закрашенную клетку. Друг от друга группы отделяются одной или
несколькими незакрашенными клетками. Строки читаются слева направо, а столбцы -
сверху вниз. Восстановите рисунок в таблице.
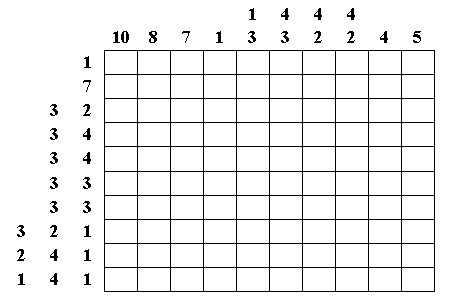
Рис. 9.
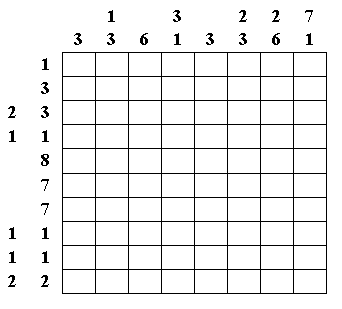
Рис. 10.
12. (5 баллов)
В прямоугольнике, разбитом на квадраты, вырезан центральный квадрат (рис. 11).
Найдите все способы разрезания данной фигуры по линиям сетки на две равные
части. Способ разрезания считается отличным от предыдущего, если он приводят к
получению новой фигуры.
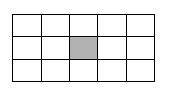
Рис. 11.
13. (4 + 6 + 8 баллов; со второй попытки - 2 + 3 + 4 балла)
Вырежьте из бумаги три одинаковых прямоугольника (рис. 12) и
а) склейте кольцо, предварительно повернув один конец на 180o;
б) склейте кольцо, предварительно повернув один конец дважды на 180o;
в) склейте кольцо, предварительно повернув один конец трижды на 180o.
Муха начинает ползти от места склейки и заканчивает свой путь там же, причем все время она ползет на равном расстоянии от краев кольца.
Для каждого случая а) - в) определите длину пути мухи.
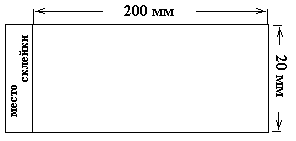
Рис. 12.
14. (10 + 10 баллов; со второй попытки - 5 + 5 баллов)
Из каждого данного вам флексагона, имеющего на лицевой стороне единицы,
получите, сгибая и разворачивая его, флексагон, у которого на лицевой стороне
будут только а) тройки; б) четверки.
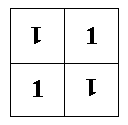
15. (15 баллов; со второй попытки - 7 балла) Из данной вам развертки получите флексагон, у которого на лицевой стороне написаны все единицы, а на оборотной - все двойки (рис.13). Модель развертки можно изготовить самостоятельно, увеличив ее размеры до нужных.
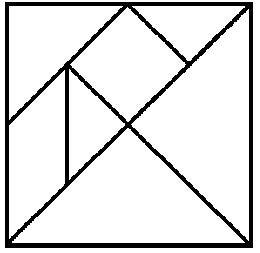
16. (по 5 баллов за каждую фигуру; со второй попытки - 2 балла) Танграмы. Полностью используя данный набор фигур, последовательно сложите фигуры, изображенные на рисунках А - Д. Накладывать фигуры или оставлять между ними пустые места нельзя, но можно их переворачивать.
 |  |  |  | 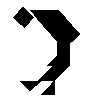 |
| А | Б | В | Г | Д |
Наборы фигур для разрезания.