Задания
Первый тур (10 минут; каждая задача - 6 баллов).
1.1. Задайте формулой какую-либо функцию f(х), которая определена при всех х, кроме тех, которые принадлежат промежутку [1; 2).
1.2. В треугольнике АВС точка А1 принадлежит отрезку ВС, а точка С1 - отрезку АВ. Может ли точка пересечения отрезков АА1 и СС1 быть серединой каждого из них?
1.3. Решите уравнение в целых числах: 1 + р + р2 + р3 = 3n.
Второй тур (15 минут; каждая задача - 7 баллов).
2.1. При всех значениях а решите уравнение: (a-|x|)1/2 + (x2-a2)1/2 = -a .
2.2. В треугольнике АВС: /А > /В > /С. К какой из вершин треугольника ближе всего расположен центр вписанной в него окружности?
2.3. На окружности расположены 1999 белых и одна красная точка. Рассмотрим все выпуклые многоугольники с вершинами в этих точках. Каких многоугольников больше: тех, у которых есть красная вершина или тех, у которых её нет?
Третий тур (15 минут; каждая задача - 7 баллов).
3.1. Найдите значение выражения (1+x+xy)-1 + (1+y+yz)-1 + (1+z+zx)-1, если известно, что хyz = 1.
3.2. Даны два лоскута материи, имеющие форму квадратов (их размеры - различны). Как их нужно раскроить, чтобы из всех получившихся кусков можно было сшить скатерть, также имеющую форму квадрата?
3.3. Найдите все такие двузначные числа x, для каждого из
которых истинны ровно три из следующих шести утверждений:
1) x делится на 3;
2) x делится на 5;
3) x делится на 9;
4) x делится на 15;
5) x делится на 25;
6) x делится на 45.
Четвертый тур (20 минут; каждая задача - 8 баллов).
4.1. При каких значениях а сумма четвёртых степеней корней уравнения х2 - х + а = 0 принимает наименьшее значение?
4.2. В прямоугольном треугольнике АВС с гипотенузой АВ, имеющей длину с, проведена высота СН. К - середина ВС. Найдите радиус окружности, проходящей через точки С, Н и К.
4.3. Каждый зритель, пришедший на спектакль "Королевский жираф", принес с собой либо одну дохлую кошку, либо два кочана гнилой капусты, либо три тухлых яйца. Стоявший у входа Гекльберри Финн подсчитал, что кошек было 64 штуки. После спектакля оба артиста - король и герцог - были с ног до головы закиданы припасами, причем на долю каждого досталось поровну предметов (а промахов жители Арканзаса не делают). Правда, король принял на себя лишь пятую часть всех яиц и седьмую часть капусты, но все дохлые кошки полетели именно в него. Сколько зрителей пришло на представление?
Пятый тур (25 минут; каждая задача - 9 баллов).
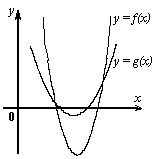
5.1. Даны графики двух квадратичных функций:
f(x) = a1x2 + b1x + c1 и
g(x) = a2x2 + b2x + c2,
имеющие одинаковые направления "ветвей". Абсциссы их точек пересечения
положительны, оси симметрии могут не совпадать (см. рис.). Сравните
соответствующие коэффициенты трехчленов.
5.2. М - внутренняя точка равностороннего треугольника АВС. Существует ли треугольник, стороны которого равны отрезкам МА, МВ и МС, а вершины лежат на сторонах данного равностороннего треугольника?
5.3. Представьте единицу в виде суммы квадратов пяти попарно различных положительных рациональных чисел.