Задания
Первый тур (10 минут; каждая задача - 6 баллов).
1.1. При каких значениях m уравнения mx-1000=1001 и 1001x=m-1000x имеют общий корень?
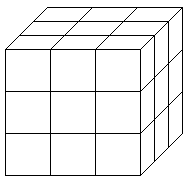
1.2. Куб сложен из 27 одинаковых кубиков (см. рис.). Сравните
площадь поверхности этого куба и площадь поверхности фигуры, которая
получится, если из него вынуть все "угловые" кубики.
1.3. Назовем натуральное число "замечательным", если оно самое маленькое среди натуральных чисел с такой же, как у него, суммой цифр. Чему равна сумма цифр две тысячи первого замечательного числа?
Второй тур (15 минут; каждая задача - 7 баллов).
2.1. Докажите, что (1/2)-(1/3)+(1/4)-(1/5)+...+(1/98)-(1/99)+(1/100)>1/5 .
2.2. Через вершины А и С треугольника АВС проведены прямые, перпендикулярные биссектрисе угла АВС. Они пересекают прямые СВ и ВА в точках К и М соответственно. Найдите длину АВ, если ВМ = 8 см, KC = 1 см и АВ > ВС.
2.3. В клетках шахматной доски записаны в произвольном порядке натуральные числа от 1 до 64 (в каждой клетке записано ровно одно число и каждое число записано ровно один раз). Может ли в ходе шахматной партии сложиться ситуация, когда сумма чисел, записанных в клетках, занятых фигурами, ровно вдвое меньше суммы чисел, записанных в клетках, свободных от фигур?
Третий тур (20 минут; каждая задача - 8 баллов).
3.1. Вася задумал три различные цифры, отличные от нуля. Петя записал все возможные двузначные числа, в десятичной записи которых использовались только эти цифры. Сумма записанных чисел равна 231. Найдите цифры, задуманные Васей.
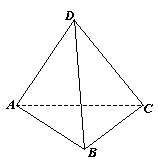
3.2. Дана пирамида АВСD (см. рис.). Известно, что
/ADB = /DBC;
/ABD = /BDC;
/BAD = /ABC.
Найдите площадь поверхности пирамиды (сумму площадей четырех треугольников), если площадь треугольника АВС равна 10 см2.
3.3. На острове проживают 1234 жителя, каждый из которых либо рыцарь (который всегда говорит правду) либо лжец (который всегда лжет). Однажды, все жители острова разбились на пары, и каждый про своего соседа по паре сказал: "Он - рыцарь!", либо "Он - лжец!". Могло ли в итоге оказаться, что тех и других фраз произнесено поровну?
Четвертый тур (25 минут; каждая задача - 9 баллов).
4.1. Расположите в порядке возрастания числа: 2222; 2222; 2222; 2222; 2222; 2222; 2222. Ответ обоснуйте.
4.2. Отрезки АС и BD пересекаются в точке О. Периметр треугольника АВС равен периметру треугольника АВD, а периметр треугольника ACD равен периметру треугольника BCD. Найдите длину АО, если ВО = 10 см.
4.3. Какое наибольшее количество прямоугольников 4*1 можно разместить в квадрате 6*6 (не нарушая границ клеток)?