Математическая регата 8 классов 12.05.2001
Задания | Результаты | План мероприятий Турнира Архимеда на 2000/2001 уч. г.
Задания
Первый тур (10 минут; каждая задача - 6 баллов).
1.1. Решите неравенство:
|x + 2000| < |x - 2001|.
1.2. Существует ли выпуклый четырехугольник, у которого сумма длин
диагоналей не меньше, чем сумма длин всех сторон?
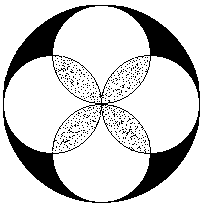
1.3. Через центр окружности проведены еще четыре окружности,
касающиеся данной (см. рис.). Сравните площади фигур, выделенных на рисунке
черным и серым цветом соответственно.
Второй тур (15 минут; каждая задача - 7 баллов).
2.1. Решите систему уравнений:
| { | 1-x1x2=0 |
| 1-x2x3=0 |
| ... |
| 1-x2000x2001=0 |
| 1-x2001x1=0 |
2.2. В остроугольном треугольнике ABC угол B равен
60o, AM и CN - его высоты, а Q - середина
стороны AC. Докажите, что треугольник MNQ - равносторонний.
2.3. Найдите все натуральные m и n, для которых
выполняется равенство:
m! +12 = n2.
Третий тур (20 минут; каждая задача - 8 баллов).
3.1. Укажите все пары (x; y), для которых
выполняется равенство:
(x4 + 1)(y4 + 1) = 4x2y2.
3.2 К окружности с диаметром АС проведена касательная
ВС. Отрезок АВ пересекает окружность в точке D. Через
точку D проведена еще одна касательная к окружности, пересекающая
отрезок ВС в точке K. В каком отношении точка K разделила
отрезок ВС?
3.3 Трое рабочих копают яму. Они работают по очереди, причем каждый
из них работает столько времени, сколько нужно двум другим, чтобы вырыть
половину ямы. Работая таким образом, они выкопали яму. Во сколько раз быстрее
трое рабочих выкопают такую же яму, если будут работать одновременно?
Четвертый тур (25 минут; каждая задача - 9 баллов).
4.1. Найдите все значения а, для которых выражения
а+151/2 и (1/а)-151/2
принимают целые значения.
4.2. Расстояние между серединами диагоналей трапеции равно 5 см,
а ее боковые стороны имеют длины 6 см и 8 см. Найдите расстояние между
серединами оснований.
4.3. Рассмотрим все моменты времени, когда часовая и минутная
стрелки часов лежат на одной прямой, образуя развернутый угол. Найдутся ли
среди таких прямых две взаимно перпендикулярные?
Результаты
Команда
школы | I | II | III | IV | Сумма
баллов | Место |
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| 2А | 6 | 6 | 1 | 7 | 2 | 2 | 8 | 8 | 0 | 0 | 1 | 9 | 50 | 6 |
| 2Б | 6 | 6 | 5 | 3 | 2 | 2 | 8 | 8 | 0 | 9 | 9 | 0 | 58 | 2 |
| 2В | 6 | 6 | 1 | 7 | 7 | 7 | 2 | 8 | 7 | 9 | 9 | 0 | 69 | 1 |
| 5 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 23-24 |
| 7А | 6 | 6 | 0 | 2 | 2 | 0 | 0 | 5 | 0 | 0 | 9 | 0 | 30 | 13 |
| 7Б | 0 | 6 | 1 | 7 | 0 | 2 | 1 | 0 | 0 | 3 | 4 | 1 | 25 | 15 |
| 109А | 6 | 0 | 0 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 10 | 20-21 |
| 109Б | 0 | 0 | 1 | 0 | 0 | 1 | 8 | 0 | 0 | 0 | 0 | 0 | 10 | 20-21 |
| 174 | 6 | 6 | 1 | 0 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 21 | 16 |
| 218 | 0 | 6 | 0 | 5 | 0 | 3 | 8 | 0 | 0 | 3 | 0 | 7 | 32 | 11 |
| 747 | 0 | 0 | 5 | 2 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 8 | 22 |
| 1018А | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 25-26 |
| 1018Б | 6 | 0 | 6 | 7 | 0 | 3 | 8 | 8 | 0 | 0 | 0 | 0 | 38 | 9 |
| 1064 | 0 | 0 | 6 | 5 | 2 | 1 | 8 | 0 | 0 | 9 | 0 | 0 | 31 | 12 |
| 1101А | 0 | 0 | 5 | 0 | 0 | 0 | 8 | 1 | 0 | 0 | 0 | 0 | 14 | 18-19 |
| 1101Б | 0 | 6 | 0 | 0 | 0 | 0 | 8 | 0 | 0 | 0 | 0 | 0 | 14 | 18-19 |
| 1106 | 0 | 6 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 23-24 |
| 1189А | 6 | 6 | 0 | 7 | 2 | 0 | 8 | 8 | 0 | 3 | 1 | 0 | 41 | 7 |
| 1189Б | 0 | 6 | 1 | 3 | 1 | 4 | 8 | 8 | 0 | 0 | 0 | 8 | 39 | 8 |
| 1514А | 6 | 6 | 0 | 7 | 0 | 2 | 8 | 8 | 0 | 9 | 3 | 6 | 55 | 3 |
| 1514Б | 6 | 6 | 5 | 7 | 7 | 7 | 6 | 8 | 0 | 0 | 0 | 0 | 52 | 5 |
| 1543А | 6 | 5 | 6 | 7 | 7 | 2 | 5 | 8 | 0 | 0 | 0 | 7 | 53 | 4 |
| 1543Б | 6 | 3 | 0 | 3 | 7 | 1 | 8 | 8 | 0 | 0 | 0 | 0 | 36 | 10 |
| Протвино | 6 | 6 | 1 | 3 | 2 | 7 | 1 | 3 | 0 | 0 | 0 | 0 | 29 | 14 |
| Смоленск | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 25-26 |
| Ступино | 6 | 6 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 15 | 17 |
