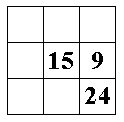
1. Магический квадрат. В клетках квадрата 3*3 были записаны натуральные числа, так, что суммы чисел в каждой строке, в каждом столбце и на каждой диагонали были одинаковыми. Некоторые числа стерли (см. рис.1). Восстановите квадрат.
2. Странное уравнение. Пусть запись a@b
обозначает наибольшее из чисел: 2a или a+b.
Решите уравнение: x@1999 = 2001@x.
3. Начертите отрезок. Как с помощью прямоугольной плитки размером 7*9 см начертить на листе бумаги отрезок, длина которого - 1 см?
4. Рыбацкий рассказ. Николай сказал: "Я поймал рыб столько же, сколько мой сын". Петр сказал: "Я поймал рыб втрое больше, чем мой сын". Известно, что никого, кроме них, на рыбалке не было, а всего поймано 49 рыб. Могут ли оба высказывания быть правдивыми? Ответ объясните.
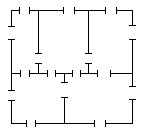
5. Царь Горох объявил, что хочет выдать замуж дочь - Василису Прекрасную. Собрались на царский двор принцы да королевичи. И сказал им царь: "Есть у меня охотничий домик (см. рис. 2), в нем пять комнат. Кто сможет обойти весь домик, пройдя через каждую дверь ровно один раз, тот и получит царевну в жены!" Можно ли выполнить условие Царя Гороха? Ответ объясните.
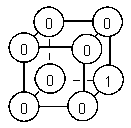
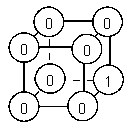
6. Числа в вершинах. В каждой вершине куба записано число.
За один шаг разрешается к каждому из двух чисел, находящихся на концах
одного (любого) ребра, прибавить по единице. Можно ли за несколько таких
шагов добиться того, чтобы все восемь чисел стали между собой равны если
вначале они были поставлены как:
а) на рис. 3?
б) на рис. 4?
 |  |  |  |
| рис. 1 | рис. 2 | рис. 3 | рис. 4 |