Математическая регата 7 классов 16.03.2002

Первый тур (10 минут; каждая задача - 6 баллов)

1.1. Число 5 возвели в степень 2002. Как вы думаете, в получившемся числе больше, чем 2002 цифры или меньше? Ответ объясните.

1.2. Две стороны и высота, проведенная к третьей стороне одного треугольника соответственно равны двум сторонам и высоте, проведенной к третьей стороне другого треугольника. Можно ли утверждать, что треугольники равны? Ответ объясните.

1.3. Водитель дальнобойного грузовика взглянул на приборы своей машины и увидел, что спидометр показывает число 25952. "Какое красивое число километров я проехал. Наверное, не скоро выпадет следующее красивое число" - подумал он. Однако, через 1 час 20 минут на спидометре высветилось следующее красивое число. С какой скоростью ехал грузовик?

Второй тур (15 минут; каждая задача - 7 баллов)

2.1. Известно, что (a-b+2002), (b-c+2002) и (c-a+2002) - три последовательных целых числа. Найдите эти числа.

2.2. Можно ли расположить на плоскости (но не на одной прямой!) пять точек так, чтобы выполнялось условие: "если три точки являются вершинами треугольника, то этот треугольник - прямоугольный"? Ответ объясните.

2.3. Автомат умеет от любого картонного прямоугольника отрезать квадрат со стороной, равной меньшей стороне прямоугольника. Петя разрезал имевшийся у него прямоугольник на 2 больших квадрата, 3 квадрата поменьше и 5 маленьких квадратов со стороной 10 см, используя только этот автомат. Найдите размеры Петиного прямоугольника.

Третий тур (20 минут; каждая задача - 8 баллов)

3.1. Может ли натуральное число иметь в полтора раза больше нечетных делителей, чем четных? Ответ объясните.

3.2. В треугольнике ABC H - точка пересечения высот AA₁ и BB₁. Найдите /ВАС, если известно, что AH=BC.

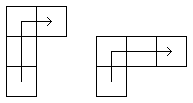
3.3. Шахматный конь хочет попасть из левого нижнего угла в правый верхний угол на доске размером 2002*2003, делая ходы только вправо и вверх (см. рисунок). Сможет ли он это сделать? Ответ объясните.

Четвертый тур (25 минут; каждая задача - 9 баллов)

4.1. Докажите, что число 11...1-22...2 (218 цифр "2" и 2*218 цифр "1") является квадратом некоторого натурального числа.

4.2. В треугольнике АВС: /В = 20^o, /С = 40^o, длина биссектрисы АМ равна 2 см. Найдите разность сторон: ВС-АВ.

Правила

1. В математической регате участвуют школьные команды учащихся параллели седьмых классов. В составе каждой команды - 4 человека. Школа может быть представлена одной или несколькими командами. Названием команды является номер школы с добавленным к нему буквенным индексом.

2. Соревнование проводится в 4 тура. Каждый тур представляет собой коллективное письменное решение трех задач. Любая задача оформляется и сдается в жюри на отдельном одинарном листе. Каждая команда имеет право сдать только по одному варианту решения каждой из задач. Листы каждая команда заготавливает заранее, на каждом из них сверху крупно написано название команды, а ниже - двойной индекс задачи и ее решение. Условия задач на этот лист не переписываются. Использование какой-либо математической литературы запрещено.

3. Проведением регаты руководит Координатор. Он организует раздачу заданий и сбор листов с решениями; проводит разбор задач и объявляет итоги проверки.

4. Время, отведенное командам для решения, и "ценность" задач каждого тура в баллах указаны на листах с условиями задач, которые каждая команда получает перед началом каждого тура.

5. Проверка решений осуществляется жюри после окончания каждого тура. Жюри состоит из трех комиссий, специализирующихся на проверке задач N 1, N 2 и N 3 каждого тура соответственно.

6. Параллельно с проверкой, Координатор осуществляет разбор задач для учащихся, а затем объявляет итоги проверки. После объявления итогов тура, команды, не согласные с тем, как оценены их решения, имеют право подать заявки на апелляции. В случае получения такой заявки, комиссия проверявшая решение, осуществляет повторную проверку и, после нее, может изменить свою оценку. Если оценка не изменена, то сам процесс апелляции эта же комиссия осуществляет после окончания всех туров регаты, но до окончательного подведения итогов. В результате апелляции оценка решения может быть как повышена, так и понижена, или же оставлена без изменения. В спорных случаях окончательное решение об итогах проверки принимает председатель жюри.

7. Команды - победители и призеры регаты определяются по сумме баллов, набранных каждой командой во всех турах. Награждение победителей и призеров происходит сразу после подведения итогов регаты.