Докажите, что в него можно вписать окружность и найдите её радиус.
Задания | Результаты | План мероприятий Турнира Архимеда на 2001/2002 уч. г.
Первый тур (10 минут; каждая задача - 6 баллов) 1.1. Известно, что число a является корнем уравнения
x3+7x-9=0.
1.2. Могут ли длины сторон a, b и c
прямоугольного треугольника удовлетворять соотношению
a2+b2=5c2 ?
1.3. Сколько десятизначных чисел можно составить так, чтобы
любые две соседние цифры отличались на единицу, если в их десятичной
записи можно использовать только цифры 1, 2 и 3 ?
Второй тур (15 минут; каждая задача - 7 баллов) 2.1. При каких натуральных значениях n выражение
n2+(n-1)2+n2(n-1)2
является полным квадратом?
2.2. Один из углов трапеции равен 60o. Найдите
отношение её оснований, если известно, что в эту трапецию можно
вписать окружность и около этой трапеции можно описать окружность.
2.3. Сравните числа A и B, не используя калькулятор:
Третий тур (15 минут; каждая задача - 7 баллов) 3.1. Решите уравнение
3.2. В треугольнике АВС:
угол А > угол В > угол С.
К какой из сторон треугольника ближе всего расположен
центр окружности, описанной около этого треугольника?
3.3. За одну операцию разрешается разрезать многоугольник
на две части по любому отрезку, перевернуть одну из частей и склеить
эти части по тому же отрезку. Можно ли за несколько таких операций из
прямоугольника 5*20 получить квадрат 10*10 ?
Четвертый тур (20 минут; каждая задача - 8 баллов) 4.1. Решите систему уравнений:
Задания
Найдите значение выражения
(2a3+3a)(11a-18).
A = 1*2*3*...*19*20 и
B = 1+2+3+...+999999+1000000.
15(x+1)=|x-1|+|x-2|+|x-3|+|x-4|+|x- 5|.
| { | x+y+z | = | 3, |
| x2+y2+z2 | = | 3. |
4.2. A и B - фиксированные точки на плоскости. Найдите геометрическое место точек M этой плоскости, для которых угол ABM - наибольший из углов треугольника ABM.
4.3. На столе поставлены в один ряд N стаканов, перевёрнутые вверх дном. Разрешается одновременно переворачивать два стакана, стоящие через один. При каких значениях N можно добиться того, чтобы все стаканы стояли дном вниз?
Пятый тур (25 минут; каждая задача - 9 баллов)
5.1. При каких значения параметра a
разность корней квадратного
x2-6x+12+a2-4a=0
принимает наибольшее значение?
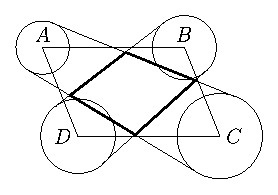
5.2. Вершины параллелограмма ABCD являются центрами
непересекающихся окружностей, радиусы которых равны соответственно
5, 6, 8 и 7 (см. рис.). К окружностям с центрами в противолежащимих
вершинах проведены общие внешние касательные, которые образуют
новый четырёхугольник.

Докажите, что в него можно вписать окружность и найдите её радиус.
5.3. Найдите среднее арифметическое всех пятизначных чисел-палиндромов (чисел, которые справа налево и слева направо читаются одинаково, например, 12421).
| команда школы | тур 1 | тур 2 | тур 3 | тур 4 | тур 5 | Итоговый балл | ||||||||||
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1514 Б | 1 | 0 | 6 | 7 | 7 | 7 | 7 | 7 | 7 | 8 | 5 | 2 | 9 | 9 | 2 | 84 |
| 1189 А | 0 | 6 | 3 | 0 | 7 | 7 | 7 | 3 | 7 | 8 | 4 | 2 | 9 | 8 | 9 | 80 |
| 1543 А | 6 | 6 | 6 | 0 | 1 | 7 | 7 | 1 | 7 | 8 | 2 | 2 | 9 | 1 | 9 | 72 |
| 91 А | 6 | 6 | 6 | 0 | 7 | 7 | 7 | 1 | 7 | 8 | 0 | 2 | 9 | 0 | 2 | 68 |
| 82 Б (Черноголовка) | 0 | 6 | 2 | 0 | 7 | 7 | 7 | 7 | 0 | 1 | 4 | 8 | 9 | 0 | 4 | 62 |
| 1543 В | 6 | 6 | 1 | 0 | 1 | 7 | 7 | 1 | 7 | 1 | 4 | 2 | 9 | 1 | 9 | 62 |
| 2 В | опозд. | 0 | 7 | 7 | 7 | 4 | 7 | 1 | 6 | 8 | 9 | 0 | 2 | 58 | ||
| Протвино | 0 | 6 | 6 | 1 | 7 | 0 | 7 | 7 | 1 | 1 | 4 | 1 | 9 | 1 | 4 | 55 |
| 2 Б | опозд. | 0 | 7 | 0 | 7 | 2 | 7 | 8 | 8 | 2 | 9 | 0 | 4 | 54 | ||
| 1189 Б | 6 | 0 | 1 | 0 | 1 | 7 | 7 | 7 | 7 | 1 | 3 | 3 | 5 | 0 | 4 | 52 |
| 82 A (Черноголовка) | 6 | 6 | 0 | 0 | 7 | 0 | 0 | 7 | 0 | 1 | 4 | 2 | 9 | 0 | 9 | 51 |
| 1101 А | 6 | 6 | 0 | 7 | 7 | 2 | 7 | 6 | 1 | 1 | 0 | 5 | 0 | 1 | 0 | 49 |
| 1514 А | 0 | 6 | 0 | 0 | 2 | 7 | 7 | 7 | 0 | 1 | 1 | 2 | 9 | 0 | 2 | 44 |
| 2 А | опозд. | 0 | 7 | 1 | 7 | 7 | 0 | 1 | 4 | 4 | 9 | 1 | 2 | 43 | ||
| 29 (Смоленск) | 4 | 6 | 0 | 0 | 7 | 1 | 0 | 0 | 1 | 1 | 0 | 8 | 9 | 0 | 4 | 41 |
| Раменское | 4 | 0 | 0 | 0 | 1 | 7 | 7 | 1 | 1 | 1 | 5 | 0 | 9 | 1 | 4 | 41 |
| 1523 | 0 | 6 | 0 | 1 | 7 | 7 | 1 | 1 | 1 | 1 | 0 | 2 | 9 | 0 | 2 | 38 |
| 1189 В | 0 | 0 | 0 | 6 | 1 | 4 | 7 | 1 | 7 | 1 | 0 | 4 | 2 | 0 | 3 | 36 |
| 91 Б | 0 | 3 | 0 | 0 | 1 | 3 | 7 | 0 | 1 | 1 | 6 | 2 | 9 | 0 | 2 | 35 |
| 218 | 0 | 0 | 2 | 0 | 1 | 0 | 7 | 1 | 1 | 8 | 0 | 4 | 9 | 0 | 2 | 35 |
| 174 | 0 | 0 | 1 | 0 | 1 | 4 | 7 | 1 | 1 | 1 | 0 | 2 | 9 | 0 | 4 | 31 |
| 7 А | 0 | 0 | 0 | 0 | 7 | 0 | 1 | 0 | 7 | 0 | 0 | 2 | 9 | 0 | 0 | 26 |
| 1543 Б | 0 | 0 | 0 | 0 | 7 | 0 | 7 | 3 | 0 | 1 | 0 | 4 | 0 | 0 | 2 | 24 |
| 1101 Б | 0 | 6 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 2 | 8 | 0 | 0 | 21 |
| 109 Б | 0 | 0 | 0 | 0 | 1 | 0 | 7 | 0 | 0 | 3 | 0 | 2 | 5 | 0 | 0 | 18 |
| 1306 | 6 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 2 | 5 | 0 | 0 | 18 |
| 109 А | 0 | 6 | 0 | 0 | 1 | 0 | 5 | 0 | 1 | 1 | 0 | 2 | 0 | 0 | 0 | 16 |
| 7 Б | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 1 | 1 | 1 | 0 | 2 | 0 | 0 | 2 | 14 |
| 17 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 2 | 0 | 0 | 0 | 7 |
| 747 А | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 2 | 0 | 0 | 0 | 5 |
| 747 Б | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 2 |
| количество верных решений | 9 | 13 | 4 | 3 | 15 | 11 | 21 | 8 | 10 | 6 | 5 | 4 | 23 | 2 | 4 | |