4. (12 баллов) ХОРОШО ИМЕТЬ ПРАВИЛЬНОГО ПАПУ
Решение. На первый взгляд задача кажется нерешаемой - в ней почти
ничего не известно! Например, не дано ни одного расстояния - как же найти
нужные скорости? Правда, сами скорости искать не надо, требуется лишь их
отношение. Неизвестные расстояния придется как-то обозначить и надеятся, что
в окончательный ответ они не войдут.
Каждый учебный день к школе из дома за Вовочкой приезжает "Мерседес".
Ровно в одно и то же время Вовочка садится в машину и едет домой. Однажды
занятия в школе закончились на час раньше, и Вовочка решил отправиться домой
пешком. По дороге он встретил едущий навстречу "Мерседес", сел в него и
вернулся домой на 10 минут раньше обычного. Во сколько раз "Мерседес"
движется быстрее Вовочки?
Обозначим школу буквой Ш, дом - Д, место встречи - В.
Известно, что "Мерседес", выехав из Д в обычное время, вернулся на 10
минут раньше. Где он сэкономил эти 10 минут? Он не проехал (туда и обратно)
расстояние ВШ. Значит, это расстояние он проехал бы туда и обратно за
10 минут, а в одну сторону - за 5 минут.
В точке В "Мерседес" встретился с Вовочкой. Если бы этого не
произошло, то через 5 минут "Мерседес" подъехал бы к школе - точно к концу
занятий. Значит, в точке В "Мерседес" был за 5 минут до обычного конца
занятий. Вовочка оказался там одновременно с "Мерседесом". Если он вышел из
школы за час до обычного конца занятий, а пришел в точку В за 5 минут
до конца, то на путь ВШ он затратил 60-5=55 минут.
Итак, Вовочка тратит на расстояние ВШ 55 минут, а "Мерседес" - 5
минут. Значит, "Мерседес" движется в 55:5=11 раз быстрее Вовочки.
Заметим, что если "Мерседес" не нарушает Правила дорожного движения и
едет со скоростью 60 км/ч, то Вовочка движется с обычной для пешехода
скоростью - около 5,5 км/ч.
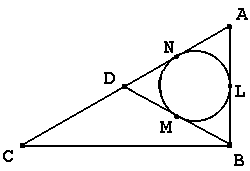
5. (10 баллов) КАЖДЫЙ ДОЛЖЕН НАЙТИ СВОЙ УГОЛ
Из вершины B прямого угла DABC
проведена медиана BD. Окружность, вписанная в
DABD, касается стороны AD в
середине. Найти углы DABC.
Решение. В прямоугольном треугольнике медиана, проведенная к
гипотенузе, равна по длине половине этой гипотенузы. Значит,
AD=BD, т. е. DABD
равнобедренный. Вписанная окружность отсекает точками касания L,
M, N на сторонах угла равные отрезки
(AL=LB=BM=MD=DN=NA).
Сравнивая эти отрезки и учитывая, что точка касания делит сторону AD
пополам, находим, что все эти 6 отрезков в
DABD одинаковы, т.е. он равносторонний.
Отсюда /РA = 60o ,
а /РC = 30o .
6. (12 баллов) ПРАКТИКУМ КАЗНАЧЕЯ
Имеется 100 монет, среди них несколько фальшивых, и рычажные весы без
гирь. Все настоящие монеты одинаковы; все фальшивые монеты также одинаковы и
весят легче настоящих. За 51 взвешивание найти количество фальшивых монет
(сами монеты отбирать не обязательно).
Решение. Эта задача оказалась более сложной. Ясно, что каждая монета
должна быть взвешена, иначе про нее ничего нельзя будет сказать. Ясно также,
что взвешивать монеты по одной бесполезно: каждую монету можно будет взвесить
лишь по разу, и если чаши весов останутся в равновесии, то взвешивание
окажется бесполезным. Можно взвешивать монеты парами, если есть подходящий
эталон. В качестве такого эталона можно взять пару из одной фальшивой и одной
настоящей монеты. На первую чашу весов кладем эталонную пару, а на вторую -
пару неизвестных монет. Если вторая чаша поднялась, обе монеты на ней
фальшивые, если опустилась - обе настоящие; если весы остались в равновесии,
на второй чаше фальшивая и настоящая монеты (мы не знаем, какая из двух
фальшивая, но нам это и не нужно).
Все это хорошо, но у нас нет эталона. Придется начинать без него.
Разобьем 100 монет на 50 пар. Выберем одну пару и положим на чаши весов по
одной монете. Если равновесие нарушилось, то монеты разные - нам повезло,
требуемый эталон найден. Сравниваем с ним остальные 49 пар, как описано выше.
Задача решена за 50 взвешиваний.
Если при первом взвешивании весы остались в равновесии, то монеты в
выбраной паре одинаковые - то ли обе фальшивые, то ли обе настоящие. Делать
нечего - используем пока эту пару в качестве эталона, взвешивая с ней
остальные пары, пока равновесие не нарушится. Так как весы при взвешиваниях
оставались в равновесии, все взвешенные до этого пары были одинаковыми и
совпадали с первой. Как только мы найдем пару, отличную от первой, мы сможем
сказать, какие монеты были в первой паре (и всех совпадающих с ней парах).
Это зависит от того, опустилась или поднялась чаша с первой парой - ясно,
что чаша с парой настоящих монет не поднимется (а с парой фальшивых не
опустится), какая бы пара ни лежала на другой чаше.
Итак, со всеми ранее взвешенными монетами мы разобрались. Теперь можно
сделать правильный эталон. Кладем на весы по одной монете из последней пары
(той, которая нарушила равновесие). Если монеты разные, требуемый эталон
найден. Если монеты одинаковые, составляем эталон из одной монеты первой пары
и одной монеты последней пары. Это действительно подходящий эталон, поскольку
известно, что эти две монеты различны. Остальные пары сравниваем с новым
эталоном, как описано выше. Здесь потребуется 51 взвешивание.