Задача 1. Кодирующие отображения и узоры Пенроуза

Кодирования и декодирования

Определение. Операцией кодирования называется следующее преобразование последовательностей из S₁. Каждый нуль в последовательности {x_n} заменяется на единицу, а каждая единица - на две цифры - 1 и 0 (именно в таком порядке), причем замены всех элементов последовательности выполняются одновременно. Например:
1, 1, 1, 0, 0, 0, ... -> 1, 0, 1, 0, 1, 0, 1, 1, 1 ...

Обозначим операцию кодирования буквой k. Операция кодирования на множестве S₂ определяется аналогичным образом. Пример:

   ..., 0, 0, 0, 1, 1, 1, 0, 0, 0, ...

..., 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, ...

Результат кодирования двусторонней последовательности определен с точностью до сдвига, хотя обычно мы будем считать, что подпоследовательность {x_n}_n>0 при кодировании переходит в подпоследовательность {у_n}_n>0.

1.1. Докажите, что существует последовательность {x_n} c S₁, такая что k({x_n})={x_n}.

Определение. Если для последовательности {x_n} c S₁ удается подобрать такую последовательность {у_n}, что {x_n}=k({у_n}), то мы будем говорить, что последовательность у_n получается из последовательности x_n декодированием. Аналогично определяется декодирование двусторонних последовательностей.

%Нетрудно сообразить, что результат декодирования определен однозначно с точностью до сдвига.

Последовательность {x_n} называется бесконечно декодируемой, если ее можно декодировать бесконечно много раз, то есть для всякого натурального m найдется такая последовательность {z_n}, что
{x_n} = k(k(...(k{z_n})...).
( операция k в правой части применена m раз ).

1.2. Докажите, что существует бесконечно декодируемая последовательность из S₂.

1.3. Докажите, что бесконечно декодируемая последовательность из S₁ непериодична.

1.4. Докажите, что множество бесконечно декодируемых последовательностей несчетно.

1.5. Докажите, что последовательности из S₂, допускающие бесконечно много декодирований, локально изоморфны. Это значит, что если в любой такой последовательности взять фрагмент конечной длины, то в любой другой такой последовательности обязательно встретится такой же фрагмент, причем бесконечно много раз.

Теперь наша цель - дать исчерпывающее описание множества последовательностей, допускающих бесконечно много декодирований.

Обозначения. Через |_-x_-| будем обозначать целую часть x, а через |^-x^-| - наименьшее целое, которое больше либо равно x.

Пусть a>1, g - вещественные числа. Положим b = a/ (a-1) (тогда a^-1+ b^-1=1). Рассмотрим двусторонние последовательности

p_n = |^-g+((n+1)/a^-| - |^-g+(n/a)^-|

p_n = |_-g+((n+1)/a_-| - |_-g+(n/a)_-|

1.6. Докажите, что
a){n: p_n=1} = {|_-a(k-g)_-|, kc{\Z}}
б){n: p_n=0} = {|^-b(k+g)^-|-1, kc{\Z}}
в){n: q_n=1} = {|^-a(k-g)^-|-1, kc{\Z}}
г){n: q_n=0} = {|_-b(k+g)_-|, kc{\Z}}.

1.7. Пусть {p_n} - двусторонняя последовательность из нулей и единиц. Для нее подобрали такую функцию j, что при каждом n
p_n=j(n+1)-j(n). Возьмем произвольный элемент p_m. При выполнении кодирования этому элементу будет соответствовать одна единица (и еще, может быть, один нуль). На каком месте в последовательности k{p_n} будет находиться эта единица?
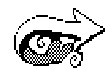Начиная с этого места, мы будем считать параметр a, использованный в формулах (1) и (2), равным "золотому сечению" (т. е. a = (1+5^1/2)/2).

1.8. Пусть {p_n} - последовательность вида (1). В качестве функции j из предыдущей задачи для такой последовательности естественно взять функцию
j(n)=|^-g+ (n/a)^-|. Докажите, что образ последовательности {p_n} при кодировании имеет вид
{|_-g^* + ((n+1)/(a)_-| - -|_-g^* + (n/a)_-|} и найдите g^*.

1.9. а) Докажите, что последовательности из задач 1.1, 1.2 - тоже последовательности вида (1), где a - по-прежнему золотое сечение. Найдите параметр g для этих последовательностей.
б) Как изменится параметр g если последовательность вида (1) сдвинуть на m символов вправо?

1.10. Пусть на координатной плоскости нанесены линии целочисленной решетки и проведена прямая y=ax. Выделим стандартный единичный квадрат с вершинами (0,0), (0,1), (1,0), (1,1) и пронесем его вдоль прямой. Квадрат заметет полосу, содержащую исходную прямую; отметим точки с целочисленными координатами, находящиеся в этой полосе, за исключением точки (0,1). Нетрудно сообразить, что существует единственная бесконечная ломаная, звенья которой параллельны координатным осям, проходящая через все отмеченные точки и не выходящая из полосы. Спроектируем эту ломаную на исходную прямую. Тогда прямая окажется разбита на отрезки двух типов: проекции горизонтальных единичных отрезков и проекции вертикальных, обозначим эти типы соответственно через 0 и 1. Докажите, что двусторонняя последовательность типов этих отрезков вдоль нашей прямой является бесконечно декодируемой.

1.11. Докажите, что любая последовательность вида (1) или (2) бесконечно декодируемая.

1.12. Докажите, что любая бесконечно декодируемая последовательность из S₁ или S₂ имеет вид (1) или (2).

1.13. Лирическое отступление. Игра "Цяньшидзы" (или "ним Витхоффа"). Есть две кучи спичек. Двое игроков по очереди берут спички из этих кучек, причем при каждом ходе игрок или берет произвольное количество спичек из одной кучи или поровну из обеих. Проигрывает тот, кто не может сделать ход. Докажите, что если начальные количества спичек в кучах равны
(|_-a n_-|, |_-bn_-|), то выигрывает второй игрок, в остальных случаях выигрывает первый. Здесь a, конечно же, по-прежнему золотое сечение, а b - сопряженный показатель:
a^-1 + b^-1 = 1.

Мозаики Пенроуза

2.1. В треугольнике ABC: AB=BC, /ABC=36^o, AC=1. В треугольнике DEF: DE=EF, /DEF=108^o, DE=a. Докажите, что AB=a, DF=1+a. Докажите также, что sin 18^o= a^-1/2, cos 36^o=a/2.

2.2. Есть конечное число типов плиток, каждая из которых представляет собой выпуклый многоугольник. Известно, что для любого r из этих плиток можно сложить фигуру, которая содержит круг радиуса r. Докажите, что тогда этими плитками можно замостить всю плоскость.

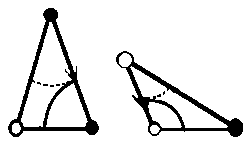
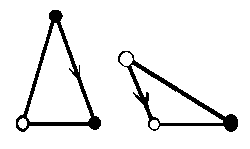
Мозаики Пенроуза можно строить для разных наборов плиток. Мы начнем с треугольных плиток. Есть два стандартных набора треугольных плиток, назовем их А-набор (слева) и Б-набор (внизу справа).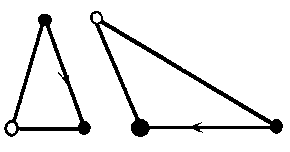 Каждый из этих наборов состоит из двух треугольников, с углами кратными 36^o. Вершины треугольников раскрашены в два цвета, стороны с одноцветными вершинами помечены стрелкой. Треугольники разрешается прикладывать друг к другу так, чтобы совмещались вершины одинакового цвета, при этом, если совмещаются стороны со стрелками, то стрелки должны иметь одинаковые направления. Треугольники разрешается поворачивать и переворачивать. Прикладывая плитки друг к другу по этим правилам, мы получим мозаику Пенроуза. Мы будем, в основном, пользоваться плитками из А-набора.

2.3. Докажите, что плитками из А-набора можно замостить всю плоскость.

2.4. Докажите, что это можно сделать не единственным способом (с точностью до движений плоскости).
Правило, по которому плитки прикладываются друг к другу при составлении мозаики, можно сделать более наглядным. Нарисуем на каждой плитке две линии так, как это показано на рисунке и потребуем, чтобы при выкладывании мозаики стороны плиток совмещались так, чтобы концы линий совпадали. Тогда на любой мозаике появится узор из линий.

2.5. Докажите, что всякая замкнутая линия из этого узора имеет симметрию пятого порядка (т. е. существует такая точка O плоскости, что узор переходит в себя при повороте на 72^o относительно точки 0).

Другой способ разметки плиток - так называемые полосы Аммана. На каждой из двух плиток можно нарисовать несколько отрезков таким образом, что при выкладывании мозаики/концы этих отрезков совмещаются и на плоскости образуется семейство прямых линий.

2.6. Придумайте такой способ разметки.

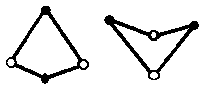Кроме упомянутых наборов из треугольников, рассматривают также набор из ромбов (с углами 72^o, 108^o и 36^o, 144^o, см. мозаику в начале текста) и набор "(воздушный) змей + дротик" . Последний набор удобен тем, что не требует введения ориентации на сторонах.

2.7. Докажите, что указанными наборами плиток можно замостить всю плоскость.

2.8.Докажите, что существует несчетное множество различных мозаик Пенроуза.

Будем говорить, что мозаика Пенроуза имеет дыру, если плитки этой мозаики покрывают всю плоскость, за исключением (не обязательно связной) фигуры конечной площади. Для такой мозаики можно попытаться увеличить дыру, сняв несколько (конечное число) плиток, после чего замостить какой-либо фрагмент непокрытой части по-другому. Мозаики с дырами, получающиеся друг из друга при помощи таких операций, будем считать эквивалентными.

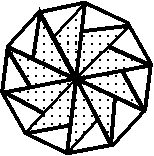
2.9. На рисунке изображена фигура "циркулярная пила", построенная из плиток Б-набора с нарушением правил совмещения плиток. Можно считать, что все вершины правильного десятиугольника одного цвета, а стороны ориентированы по часовой стрелке. Докажите, что существует мозаика с дырой в виде циркулярной пилы.

2.10. Докажите, что никакая мозаика с дырой в виде циркулярной пилы не эквивалентна мозаике без дыр.

2.11. a) Рассмотрим семейство параллельных прямых Аммана. Докажите, что расстояния между соседними прямыми в этом семействе принимают ровно два различных значения.
б) Сопоставим этим расстояниям числа 0 и 1 и выпишем последовательность, в которой эти расстояния встречаются в нашем семействе прямых. Докажите, что эта последовательность бесконечно декодируемая.