8 класс. Лига А.
1. На большом приеме в посольстве собралось 2004 человека. Известно, что среди любой четверки людей найдутся трое, знакомые друг с другом, или трое, незнакомые друг с другом. Докажите, что среди этих людей можно найти 1002, которые все знакомы друг с другом, или все незнакомы друг с другом.
2. Докажите, что каждое натуральное число можно представить в виде разности двух взаимно простых составных чисел.
3. На плоскости расположены n точек. Через каждые две точки проведена прямая. Оказалось, что проведено 20 различных прямых. При каком наименьшем n это возможно?
4. Докажите неравенство: ![]()
5. На доске написано уравнение ... x2+ ... x +... = 0. Двое по-очереди расставляют коэффициенты в этом уравнении (коэффициент 0 перед x2 ставить нельзя). Если у получившегося уравнения нет корней, то выигрывает первый игрок, а если есть --- второй. Кто выигрывает при правильной игре?
6. За круглым столом сидят n³ 5 человек. Докажите, что их можно пересадить так, чтобы у каждого человека изменились оба его соседа.
7. Точки A' и B' лежат на стороне AB остроугольного треугольника ABC. Докажите, что расстояние от центра описанной окружности треугольника ABC до прямой AB меньше, чем расстояние от~центра описанной окружности треугольника A'B'C до этой прямой.
8. Точка M - середина стороны AB треугольника ABC. Точка N лежит на стороне AC, причем Ð ANM=Ð BNC. Найдите отношение MN:NB.
8 класс. Лига Б.
1. Можно ли провести на плоскости 2004 прямые, чтобы каждая пересекалась ровно с 1999 другими?
2. В классе 32% всех учеников не имеют троек по алгебре, а 48% всех учеников не имеют троек по геометрии. 50% троечников имеют две тройки: и по алгебре, и по геометрии. По другим предметам ни у кого троек нет. Сколько процентов учеников класса учится без троек?
3. Круглый торт весом 1 кг разрезан на части тремя прямолинейными оразрезами. Известно, что два из этих разрезов проходят через центр торта, а третий не проходит. Докажите, что вес по крайней мере одной части не меньше 1/6 кг.
4. Сколько существует трёхзначных чисел, цифры которых расположены в порядке убывания?
5. В прямоугольном треугольнике АВС биссектриса угла А перпендикулярна одной из медиан. Чему может быть равна градусная мера угла А?
6. Перед выборами все n кандидатов в депутаты сделали заявления. Первый кандидат заявил: "Не считая меня, среди кандидатов лжецов на одного больше, чем честных людей". Второй сказал: "Не считая меня, среди кандидатов лжецов на два больше, чем честных людей". Третий: "Не считая меня, среди кандидатов лжецов на три больше, чем честных людей". И таким образом высказались все кандидаты. Последний сказал: "Не считая меня, среди кандидатов лжецов на n больше, чем честных людей". Сколько было кандидатов в депутаты?
7. Постройте равнобедренный треугольник по основаниям биссектрис его углов.
8. Найдите все натуральные числа ![]() ,
, ![]() и
и ![]() такие, что число
такие, что число ![]() - целое.
- целое.
9 класс. Лига А.
1. Дан треугольник ABC. На продолжении стороны BC за точку B взяли такую точку D, что BD=BA, точка M - середина стороны AC. Биссектриса угла ABC пересекает прямую DM в точке P. Докажите, что углы BAP и ACB равны.
2. Докажите, что каждое натуральное число можно представить в виде разности двух взаимно простых составных чисел.
3. Действительные числа x, y, z удовлетворяют условиям x+y+z=6 и xy+yz+xz=9. Докажите, что 0£ x£ 4.
4. Две окружности w1 и w2 пересекаются в точках A и B. Окружность w2 проходит через центр окружности w1. Касательная к окружности w2, проведенная через точку B, пересекает окружность w1 в точке C (отличной от B). Докажите, что AB=BC.
5. На плоскости расположены n точек. Через каждые две точки проведена прямая. Оказалось, что проведено 20 различных прямых. При каком наименьшем n это возможно?
6. Решите систему уравнений: 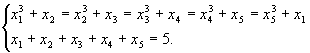 .
.
7. В стране 2004 города, любые два города соединены авиалинией. Цены билетов на всех авиалиниях различны. Могут ли все круговые маршруты (проходящие через каждый город ровно по одному разу и возвращающиеся в исходный пункт) иметь одинаковую стоимость?
8. На некоторых полях шахматной доски стоят столбики из шашек. За один ход разрешается переставить любой столбик на столько клеток по вертикали или горизонтали, сколько в нем шашек; при этом, если столбик попал на непустую клетку, он ставится на верх стоящего там столбика и объединяется с ним. Вначале на каждой клетке стоит по одной шашке. Можно ли за 63 хода собрать все шашки в один столбик?
9 класс. Лига Б.
1. Докажите, что для любого x верно неравенство x4 - x3 + 3x2 - 2x + 2 >0.
2. Петя, Коля и Вася решали задачи из задачника и решили вместе 100 задач, при этом каждый из них решил ровно 60 задач. Будем называть задачу, которую решили все трое, "легкой", а задачу, которую решил только один из них, - "трудной". На сколько "трудных" задач больше, чем "легких"?
3. С квадратным трехчленом ax2+ bx + c разрешается производить такие операции:
1) Заменить в нем x на x - a , где a - произвольное действительное число.
2) Заменить его на трехчлен сx2+ (b + 2с)x + (а + b + c).
Можно ли с помощью таких операций из трехчлена x2- 3x + 4 получить трехчлен x2- 2x - 5?
4. Все числа от 1 до 2n выписаны в строчку (в каком-то порядке). Затем к каждому числу прибавили номер места, на котором оно стоит. Докажите, что среди полученных сумм найдутся хотя бы две, разность которых делится на 2n.
5. Дан треугольник ABC. Вписанную в него окружность спроецировали на прямые, содержащие стороны треугольника. Докажите, что шесть концов проекций лежат на одной окружности.
6. Каждая грань кубика разделена на четыре квадрата. В каждый из этих квадратов вписано число. При этом любое число, вписанное в любой из 24 квадратов, в сумме с числами, вписанными в четыре соседних с ним квадрата, всегда дает 13. Могут ли все 24 числа быть целыми?
7. Как должна двигаться ладья по шахматной доске, чтобы побывать на каждом поле ровно один раз и сделать наименьшее число поворотов?
8. В ромбе ABCD на отрезке BC нашлась точка Е такая, что АЕ = CD. Отрезок ЕD пересекается с описанной окружностью треугольника АЕВ в точке F. Докажите, что точки А, F и С лежат на одной прямой.
10 класс. Лига А.
1. В некотором государстве между некоторыми городами проложены дороги. Из каждого города выходят дороги не менее чем в n других городов. Кроме того, известно, что, выехав из города, необходимо проехать не менее чем по пяти различным дорогам, для того, чтобы вернуться назад. Докажите, что общее число городов не может быть меньше ![]() .
.
2. Найдите все пары положительных чисел (х, у), удовлетворяющие равенству ![]() .
.
3. Докажите, что из любых 145 точных квадратов натуральных чисел можно выбрать 17, сумма которых делится на 17.
4. Клетки квадрата 9х9 раскрасили в шахматном порядке. Сколькими способами можно поставить на полученную доску восемь ладей так, чтобы они стояли на клетках одного цвета и не били друг друга?
5. Функция f(x) определена на всей числовой оси и такова, что f(x + 3) £ f(x) + 3 и f(x + 2) ³ f(x) + 2 для любого x. Докажите, что функция g(x) = f(x)-x - периодическая.
6. В треугольнике каждая биссектриса делится точкой пересечения биссектрис в одном и том же отношении. В каком именно?
7. На плоскости заданы 2004 полуплоскости, внутренности которых покрывают всю плоскость. Докажите, что из этих полуплоскостей можно выбрать три, внутренности которых тоже покрывают всю плоскость.
8. В магазине продаются 2004 ненулевых пространственных векторов. Вася хочет купить три некомпланарных вектора. Он поступает так: выбирает самый дешевый из них, потом самый дешевый из неколлинеарных с первым, и, наконец, самый дешевый из некомпланарных с двумя первыми. Верно ли, что Вася совершил самую выгодную покупку?
10 класс. Лига Б.
1. При каких натуральных n имеет целые решения уравнение х2 + ху + у2 = 7n.
2. В параболу у = х2 вписан прямоугольный треугольник, гипотенуза которого параллельна оси ОХ. Чему может быть равна высота треугольника, опущенная на гипотенузу?
3. а1 + а2 + а3 + а4 = 1, ![]()
![]() 0. Докажите, что
0. Докажите, что ![]() .
.
4. Из середин сторон остроугольного треугольника проведены перпендикуляры к соседним сторонам. Полученные шесть прямых ограничивают шестиугольник. Докажите, что его площадь равна половине площади исходного треугольника.
5. В конечной последовательности действительных чисел сумма любых семи идущих подряд членов отрицательна, а сумма любых одиннадцати идущих подряд членов положительна. Найдите наибольшее число членов такой последовательности.
6. На доске нарисованы 2004 квадратов, 2005 кругов и 2006 треугольников. Играют два игрока, которые делают ходы по очереди. За один ход разрешается стереть две различные фигуры и вместо них нарисовать одну фигуру, отличную от стертых (круг вместо квадрата и треугольника, квадрат вместо круга и треугольника, треугольник вместо круга и квадрата). Первый игрок выигрывает, если в результате таких операций на доске останутся только квадраты, второй - только круги. Если останутся только треугольники - ничья. Кто выигрывает при правильной игре?
7. В выпуклом четырехугольнике АВСD Ð А = Ð D. Серединные перпендикуляры к сторонам АВ и СD пересекаются в точке Р, лежащей на стороне АD. Докажите, что диагонали АС и ВD равны.
8. Пусть М - множество значений многочлена х2 + 1 в целых точках. Докажите, что множество М не содержит ни одной бесконечной (непостоянной) геометрической прогрессии.
11 класс. Лига А.
1. 25 шахматистов играют в разную силу, и при встрече любых двух всегда побеждает сильнейший. Найти минимальное число партий, при любом исходе которых можно определить первого и второго по силе.
2. BH - высота равнобедренного треугольника ABC (AB=BC), M - середина стороны AB, K - вторая точка пересечения прямой BH с окружностью BMC. Докажите, что BK=3/2R, где R - радиус окружности, описанной около треугольника ABC.
3. По аллее длиной 100 м идут три джентльмена со скоростями 1, 2, 3 км/ч. Дойдя до конца аллеи, каждый из них поворачивается и идет обратно с той же скоростью. Доказать, что найдется отрезок времени в 1 мин, когда все трое будут идти в одном направлении.
4. Бесконечная в обе стороны последовательность {an} удовлетворяет условию an=(an-1+an+1)/4. Доказать, что если в последовательности есть пара равных членов, то таких пар бесконечно много.
5. Внутри равностороннего (не обязательно правильного) 11-угольника A1A22...A11 взята произвольная точка O. Из нее опущены перпендикуляры на стороны 11-угольника. Их основания H1, H2, ... , H11 лежат соответственно на сторонах A1A2, A2A3,..., A10A11 (а не на их продолжениях). Докажите, что A1H1+A2H2+...+A11H11=H1A2+H2A3+...+H11A1.
6. Какое наибольшее число осей симметрии может иметь пространственная фигура, состоящая из трёх прямых, попарно не параллельных и не совпадающих?
7. Дана бесконечная шахматная доска с клетками 1х1. По сторонам клеток проведена замкнутая несамопересекающаяся ломаная, внутри которой оказалось k чёрных клеток. Какую наибольшую площадь может иметь фигура, ограниченная этой ломаной?
8. Даны 12 чисел a1, ..., a12, причем выполнены следующие неравенства: a2(a1-a2+a3)<0; a3(a2-a3+a4)<0; ...; a11(a10-a11+a12)<0. Докажите, что среди этих чисел найдётся по крайней мере 3 положительных и 3 отрицательных.
11 класс. Лига Б.
1. Положительные числа x, y и z таковы, что arctg x + arctg y + arctg z<p. Докажите, что тогда сумма этих чисел больше, чем их произведение.
2. Пятиугольник ABCDE, в котором BC=CD, вписан в окружность. Пусть P - точка пересечения диагоналей AC и BE, Q - точка пересечения диагоналей AD и CE. Докажите, что прямые PQ и BD параллельны.
3. У числа 22004 зачеркнули его первую цифру и прибавили ее к оставшемуся числу. С результатом проделали ту же операцию и т.д., до тех пор, пока не получили 10-значное число. Докажите, что в нем есть 2 одинаковые цифры.
4. Существует ли многогранник, у которого вершин, ребер и граней столько же, сколько у куба, но нет ни одной четырехугольной грани?
5. В параболу y=x2 вписан прямоугольный треугольник, гипотенуза которого параллельна оси ОХ. Чему может быть равна высота треугольника, опущенная на гипотенузу?
6. Докажите, что если неотрицательные числа x1, ... , x100 удовлетворяют неравенству x1+x2+...+x100 £1/2, то (1-x1)(1-x2)...(1-x100)³ 1/2.
7. В обществе, состоящем из 2004 человек, среди любых четырех человек можно выбрать по-крайней мере одного, знакомого с остальными тремя. Каково минимально возможное количество людей, которые знакомы со всеми?
8. Некоторые из клеток таблицы 100x100 отмечены. Определите число отмеченых клеток, если известно, что каждая клетка граничит по стороне ровно с одной из отмеченных.