Условия задач финала турнира математических боев

См. также результаты финала

лига 8А		лига 9A (PDF)		лига 10А		лига 11A
лига 8Б		лига 9Б		лига 10Б		лига 11Б

Лига 8А

1. Делимость. Натуральное число обладает тем свойством, что при вычеркивании любой его цифры получается число, делящееся на 7. Докажите, что либо оно записано одними четверками, либо в его записи нет ни одной четверки.

2. Отношение. В прямоугольном треугольнике АВС угол С = 90º. К - середина АВ, на стороне ВС взяли N такое, что 2*СN = NB. Найдите отношение AN:KN.

3. Набор. Набор из 2007 чисел обладает свойством: если каждое число заменить на сумму остальных, то получится тот же набор чисел. Чему равно произведение чисел в наборе?

4. Цены. Две хозяйки покупали молоко каждый день в течение месяца. Цена на молоко ежедневно менялась. Средняя цена за месяц оказалась равной 20 руб. за литр. Ежедневно первая хозяйка покупала 1 л молока, а вторая - на 20 руб. Кто из них потратил за этот месяц больше денег и кто купил больше молока?

5. Доска. В клетках шахматной доски Петя в произвольном порядке расставил числа от 1 до 64. Миша может выбрать произвольное множество клеток и узнать у Пети множество чисел, стоящих в этих клетках. За какое наименьшее число вопросов Миша может гарантированно узнать расположение всех чисел?

6. Танцы. Танцуют 5 мальчиков и 5 девочек парами (мальчик с девочкой). Может ли так случиться, что каждый из десяти танцующих в каждом следующем танце танцует с более умным или с более красивым партнером, а большинство из них танцует и с более умным, и более красивым партнером, чем в предыдущем танце? (Число танцев не ограничено.)

7. Лабиринт. В лабиринте конечное число пещер. Из каждой пещеры есть три выхода. Минотавр, заходя в пещеру, поворачивает поочередно то налево, то направо. Докажите, что Минотавр обязательно вернется в пещеру, из которой он начал свой путь.

8. Переливания. На Олимпе есть игра: всем богам наливают поровну нектара, затем один бог переливает другому столько нектара, сколько у того уже было, и это повторяется несколько раз. Однажды удалось слить весь нектар в чашу Зевса. Докажите, что число богов было степенью двойки.

Лига 8Б

1. Последовательность из 36 нулей и единиц начинается с пяти нулей. Известно, что среди пятерок подряд стоящих цифр встречаются все 32 возможные комбинации. Найдите пять последних цифр в последовательности.

1	1
	3

2. Магический квадрат - таблица 3 ´  3, заполненная числами так, что суммы во всех строках, во всех столбцах и двух диагоналях равны. Три числа известны. Можно ли однозначно восстановить остальные числа?

3. Целые числа m, n и k таковы, что k²-m²-n²=2(m-n)(k-m+n). Докажите, что число 2mn есть точный квадрат.

4. Существует ли ряд из 2006 различных чисел, в котором сумма любых трех подряд идущих чисел равняется 2005, 2006 или 2007?

5. Коля, Миша, Дима надкусали все яблоки. Число яблок, надкусанных Колей, в 2 раза больше надкусанных Димой и в 3 раз больше надкусанных Мишей. Более четверти яблок надкусано двумя из них. Верно ли, что есть яблоко, надкусанное Колей, которое надкусил кто-то еще?

6. Дан треугольник ABC. Перпендикуляры, восстановленные к сторонам AB и AC в точках B и C, пересекаются в точке A₁; перпендикуляры, восстановленные к сторонам BA и BC в точках A и C, - в точке B₁; перпендикуляры, восстановленные к сторонам CA и CB в точках A и B, - в точке C₁. Докажите, что треугольники ABC и A₁B₁C₁ равны.

7. В каждом из двух равных правильных 16-угольников отмечено по 7 вершин. Верно ли, что можно так наложить эти многоугольники друг на друга, чтобы не менее четырех отмеченных вершин одного многоугольника совпали с отмеченными вершинами другого многоугольника?

8. Какое наименьшее количество фруктов восьми различных видов можно выложить в ряд так, чтобы для любых двух видов A и B нашлось два лежащих рядом фрукта, один из которых A, а второй - B?

Лига 9Б

1. Даны колья, веревки, кольца. Коза съедает все, до чего дотянется. "Забор" из веревок, кольев и так далее строить нельзя. Как расставить колья и привязать веревки с кольцами, чтобы коза могла съесть всю внутренность произвольного треугольника и только ее?

2. Дана полоска 1*99, разбитая на 99 клеток 1*1, клетки которой раскрашены через одну в черный и белый цвет. Разрешается перекрашивать одновременно все клетки некоторой полоски 1*k. За какое наименьшее число перекрашиваний можно сделать всю полоску одноцветной?

3. Вам пришло зашифрованное сообщение: Ф В М Е Ж Т И В Ф Ю. Найдите исходное сообщение, если известно, что шифропреобразование заключалось в следующем. Пусть x₁, x₂ - корни трехчлена x²+3x+1. К порядковому номеру каждой буквы в стандартном русском алфавите (33 буквы) прибавлялось значение многочлена f(x)=x⁶+3x⁵+x⁴+x³+4x²+4x+3, вычисленное либо при x=x₁, либо при x=x₂ (в неизвестном нам порядке), а затем полученное число заменялось соответствующей ему буквой.

4. На плоскости нарисованы два квадрата - ABCD и KLMN (их вершины перечислены против часовой стрелки). Докажите, что середины отрезков AK, BL, CM, DN также являются вершинами квадрата.

5. На плоскости даны отрезок AB и точка С. Найти множество точек M, таких, что r(M,C)=r(M,AB), где r(M,C) - расстояние между M и C, а r(M,AB) - кратчайшее расстояние от M до AB.

6. Докажите, что уравнение x²+y³=z⁵ имеет бесконечно много решений в натуральных числах.

7. Антиквар приобрел 99 одинаковых по виду старинных монет. Ему сообщили, что ровно одна из монет - фальшивая - легче настоящих (а настоящие весят одинаково). Как, используя чашечные весы без гирь, помочь антиквару за 7 взвешиваний выявить фальшивую монету, если антиквар не разрешает никакую монету взвешивать более двух раз?

8. На листе бумаги нарисован выпуклый многоугольник M периметра P и площади S. Взяли круг радиуса R с центром в каждой точке, лежащей внутри этого многоугольника, и закрасили его. Найдите площадь закрашенной фигуры F.

Лига 10А

1. В графе k ребер. Докажите, что в нем не более k^3/2 треугольников.

2. Внутрь правильного 2n-угольника P с центром O и стороной 2 помещен произвольным образом правильный 2n-угольник P' со стороной 1. Докажите, что P' накрывает точку O.

3. Дана окружность, касающаяся ее прямая l и точка M на l. Найдите геометрическое место вершин C треугольников ABC, описанных около данной окружности, у которых основание AB лежит на l, а CM является медианой.

4. Дано n магнитофонных катушек, на которые намотаны ленты красными концами наружу, и 1 пустая катушка. При каких n можно перемотать все ленты так, чтобы каждая оказалась на своей катушке, но красным концом внутрь? (Перематывать можно с любой катушки на пустую в данный момент катушку, при этом наружный конец становится внутренним, и наоборот.)

5. "Инкубатор" - это прибор, позволяющий находить действительные корни любого кубического многочлена P(x). Как с его помощью найти корни многочлена P(P(x))-x?

6. Муха села в полдень на секундную стрелку часов и решила ездить, придерживаясь следующего правила: если одна стрелка обгоняет другую и муха сидит на одной из этих стрелок, то она пересаживается на другую. Сколько оборотов сделает муха к полуночи?

7. Пусть A(n)=n³-n+1. Докажите, что для любого натурального числа n, большего 1, числа n, A(n), A(A(n)), ... попарно взаимно просты.

8. Существует ли ограниченная последовательность (x_n), такая что для любых натуральных k, l выполнено неравенство |x_k-x_l|>|k-l|^-1?

Лига 10Б

1. Можно ли выбрать 100 последовательных чётных чисел и разбить их на пары (a₁,b₁),(a₂,b₂),..., (a₅₀,b₅₀) так, чтобы каждое из уравнений x²+a₁x+b₁=0, x²+a₂ x+b₂=0, ..., x²+a₅₀x+b₅₀=0 имело целые корни?

2. В треугольнике ABC проведены бисссектриса AL, высота BH и медиана CM. Оказалось, что углы CAL, ABH и BCM равны. Какие углы мог иметь треугольник ABC?

3. Решить систему уравнений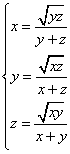

4. В клетках шахматной доски Петя в произвольном порядке расставил числа от 1 до 64. Миша может выбрать любое множество клеток и узнать у Пети множество чисел, стоящих в этих клетках. За какое наименьшее количество вопросов он сможет узнать расположение всех чисел?

5. Дан треугольник ABC. Найдите внутри него точку O, обладающую следующим свойством: для любой прямой, проходящей через точку O и пересекающей стороны треугольника AB в точке K и BC в точке L, выполняется равенство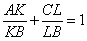

6. Было 8 гирь массами 1г, 2г,...,8г без надписей. Одну из гирь потеряли. Известно, что чем больший вес имела гиря, тем больше был её размер. Можно ли за два взвешивания на чашечных весах определить, какая из гирь потерялась?

7. Найти все многочлены P(x), для которых P(0)=0 и верно тождество P(x)=(P(x+1)+P(x-1))/2. Учитель пишет на доске произвольный многочлен P(x) с целыми неотрицательными коэффициентами. Рассматривается последовательность чисел: a₁ - сумма цифр числа P(1), a₂ - сумма цифр числа P(2) и т.д., a_n - сумма цифр числа P(n). Верно ли, что найдётся число, которое в этой последовательности встретится бесконечное количество раз?

8. Есть шоколадка в форме равностороннего треугольника со стороной n, разделённая бороздками на равностронние треугольники со стороной 1. Играют двое. За один ход можно отломать от шоколадки треугольный кусок вдоль бороздки, съесть его, а остаток передать противнику. Тот, кто получит последний кусок -- треугольник со стороной 1, - победитель. Тот, кто не может сделать ход, досрочно проигрывает. Кто выигрывает при правильной игре?

Лига 11А

1. В графе k ребер. Докажите, что в нем не более 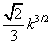треугольников.

2. Дана окружность и точка P внутри нее. Найдите геометрическое место вершин D равногранных тетраэдров ABCD, основание ABC которых вписано в данную окружность и имеет центр тяжести в точке P.

3. Дано n магнитофонных катушек, на которые намотаны ленты красными концами наружу, и 1 пустая катушка. При каких n можно перемотать все ленты так, чтобы каждая оказалась на своей катушке, но красным концом внутрь? (Перематывать можно с любой катушки на пустую в данный момент катушку, при этом наружный конец становится внутренним, и наоборот.)

4. Докажите для любых x, y, z Î [0,1] неравенство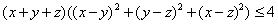

5. Докажите, что число 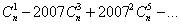(верхний индекс пробегает все нечетные значения, не превосходящие n) делится на 2^n-1.

6. "Инкубатор" - это прибор, позволяющий находить действительные корни любого кубического многочлена P(x). Как с его помощью найти корни многочлена P(P(x))-x?

7. Можно ли поместить куб в некоторый прямой круговой конус так, чтобы семь вершин куба лежали на боковой поверхности конуса?

8. Муха села в полдень на секундную стрелку часов и решила ездить, придерживаясь следующего правила: если одна стрелка обгоняет другую и муха сидит на одной из этих стрелок, то она пересаживается на другую. Сколько оборотов сделает муха к полуночи?

Лига 11Б

1. В течение 92 дней авиакомпания ежедневно выполняла по 10 рейсов. За сутки каждый самолет выполнял не более одного рейса. Известно, что для любых двух дней имеется один и только один самолет, летавший в оба эти дня. Докажите, что имеется самолет, летавший во все дни.

2. Пусть х и у - такие действительные числа, что х² + у², х³ + у³ и х⁴ + у⁴ - рациональные числа. Докажите, что ху тоже рациональное число.

3. Докажите, что произведение расстояний от центра вписанной окружности до вершин треугольника равно произведению квадрата диаметра вписанной окружности на радиус описанной окружности.

4. Докажите, что для любого натурального n сумма обратных величин первых n чисел Фибоначчи меньше 4. (Напомним, что числа Фибоначчи f_n определяются правилом f₁ = f₂ = 1, f_n+2 = f_n+1 + f_n, n > 2).

5. Клетки доски m 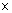n (m, n > 2) покрашены в черный и белый цвета. Гусеница заползает на угловую клетку и один раз в минуту переползает на соседнюю по стороне клетку. После того, как она покидает клетку, эта клетка меняет свой цвет. Верно ли, что гусеница может проползти по всем клеткам доски и уползти с одной из угловых клеток наружу так, чтобы все клетки доски оказались покрашены в черный цвет?

6. Даны окружность O, точка A, лежащая на ней, перпендикуляр к плоскости окружности O, восставленный из точки A, и точка B, лежащая на этом перпендикуляре. Найдите геометрическое место оснований перпендикуляров, опущенных из точки A на прямые, проходящие через точку B и произвольную точку окружности O.

7. Найдите все неубывающие функции f : 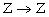такие, что f(n) + f(f(n)) = 2n + 3 при всех целых n.

8. Может ли сумма квадратов десяти подряд идущих натуральных чисел быть точным квадратом?
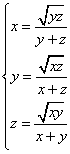