-
В противоположных углах шахматной доски стоят две ладьи.
Два игрока поочерёдно двигают ладьи, каждый свою. Нельзя проходить
через поле, находящееся под боем другой ладьи, или останавливаться на таком поле. Проигрывает тот,
кто не может сделать ход. Кто победит, если игроки не делают ошибок?
-
В треугольнике ABC точка M лежит на стороне AC, точки C1, B1,
M1, M2 – середины отрезков
AB, AC, MC, MB соответственно, C1M1=
B1M2.
Докажите, что треугольник ABC – прямоугольный.
-
В шахматном турнире каждый участник встречался с каждым один раз (победа – 1
очко, поражение – 0, ничья – пол-очка). Единоличным чемпионом стал Федя. Сеня
сказал: "Если из турнирной таблицы удалить любого участника и вычеркнуть очки,
набранные во встречах с ним, то чемпионом будет уже не Федя". Может ли Сеня
быть прав?
-
Между городами области проведено 300 дорог. Из любого города в любой другой можно проехать, пользуясь этими дорогами.
Все дороги надо распределить между 7 бригадами ремонтников так, чтобы каждая бригада ремонтировала не менее
25 дорог и могла передвигаться по своим
дорогам, не пользуясь чужими. При любой ли схеме дорог их можно так распределить между бригадами?
-
Расстояние между двумя параллельными прямыми l и m равно 1.
Сторона квадрата ABCD также равна 1. Вершины A и C
лежат в полосе между l и m, а вершины B и D – вне полосы.
Стороны AB и BC пересекают l в точках X и Y, а стороны CD и
AD пересекают m в точках Z и T соответственно. Докажите, что
угол между прямыми XZ и YT равен 45o.
-
Существуют ли такие натуральные числа a, b, c, d,
что каждое из них делится на разность любых двух других?
-
Треугольник разрезан на несколько выпуклых многоугольников. Докажите, что
среди них либо есть треугольник, либо есть два многоугольника с одинаковым числом сторон.
-
Три ненулевых числа x, y и z таковы, что x2–y2=yz и
y2–z2=xz.
Докажите, что x2–z2=xy.
-
Андрей, Борис, Василий, Геннадий и Дмитрий играли в настольный теннис парами так,
что каждые двое сыграли с каждой другой парой один раз. Ничьих в теннисе не бывает.
Андрей в общей сложности проиграл 12 раз, а Борис – 6 раз. Сколько раз выиграл Геннадий?
-
ABCD – параллелограмм. Найдите его углы, если известно, что AD=2DB,
а Ð
ABD в три раза больше, чем Ð
DBC.
-
Одна из цифр четырехзначного натурального числа – ноль.
При вычеркивании нуля это число уменьшается в девять раз. Найдите все такие числа.
-
Какие числа можно поставить вместо знака * в текст задачи:
"На плоскости даны n различных прямых, пересекающихся в * точках. Найдите значение n,
чтобы эта задача имела единственное решение?
-
На острове рыцарей и лжецов 60 жителей собрались в кинотеатре.
40 островитянам фильм не понравился, и они по очереди выходили из зала. Выходя, каждый говорил билетёру:
"Среди оставшихся в зале лжецов больше, чем рыцарей". Сколько лжецов пришло в кинотеатр?
-
Коля и Сергей по очереди записывают целые числа в клетки таблицы,
в которой 7 строк и 9 столбцов. Первым ходит Коля. Игра продолжается, пока числа не заполнят всю таблицу.
Потом подсчитываются суммы чисел в строках таблицы. Если среди них больше чётных, то выиграл Коля,
иначе – Сергей. Кто выиграет?
-
На бесконечной шахматной доске фигура "осёл" ходит на 1 клетку по горизонтали и n
по вертикали (или наоборот). При каких 1 £
n £
7 осёл сможет за несколько ходов попасть из клетки в какую-то соседнюю с ней по стороне?
-
Было 8 гирь массами 1г, 2г, ... , 8г без надписей. Одну из гирь потеряли.
Известно, что чем больший вес имела гиря, теи больше был ее размер. Как за два взвешивания на чашечных
весах выяснять, какая именно гиря потеряна?
-
В противоположных углах шахматной доски стоят две ладьи.
Два игрока поочерёдно двигают ладьи, каждый свою. Нельзя проходить
через поле, находящееся под боем другой ладьи, или останавливаться на таком поле. Проигрывает тот,
кто не может сделать ход. Кто победит, если игроки не делают ошибок?
-
В треугольнике ABC вершины A и C, центр вписанной окружности и центр
описанной окружности лежат на одной окружности. Найдите ÐB.
-
Для положительных чисел x1³ x2³...³ xn>0 докажите неравенство:
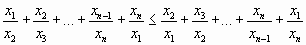
-
Между городами области проведено 300 дорог. Из любого города в любой другой можно проехать, пользуясь этими дорогами.
Все дороги надо распределить между 7 бригадами ремонтников так, чтобы каждая бригада ремонтировала не менее 25 дорог
и могла передвигаться по своим
дорогам, не пользуясь чужими. При любой ли схеме дорог их можно так распределить между бригадами?
-
Может ли число, записываемое несколькими единицами, иметь ровно
2007 различных делителей?
-
На плоскости даны точки A и B. Найдите ГМТ вершин С остроугольных треугольников АВС, у
которых высота, проведённая из вершины B, равна медиане, проведённой из
вершины A.
-
Назовем натуральное число удачным, если оно делится на любую свою ненулевую
цифру. Какое наибольшее количество удачных чисел может идти подряд?
-
Треугольник разрезан на несколько выпуклых многоугольников. Докажите, что
среди них либо есть треугольник, либо есть два многоугольника с одинаковым
числом сторон.
-
Даны два квадратных трехчлена: x2 + 2bx + с = 0 и x2 + 2cx + b = 0, b и c > 0. Известно, что произведение корней этих квадратных трехчленов равно 1. Найдите b и c.
-
На столе лежит куча из 1001 камня. Ход состоит в том, что из какой-либо кучи, содержащей более одного камня, выкидывают камень, а затем одну из куч делят на две. Можно ли через несколько ходов оставить на столе только кучки, состоящие из трех камней?
-
В окружности проведены две пересекающиеся хорды AB и CD. На хорде AB взята точка
M так, что AM = AC, а на хорде CD – точка N такая, что DN = DB. Докажите, что если точки M и N не совпадают, то прямая MN параллельна прямой AD.
-
В деревне Гадюкино у каждого мальчика все знакомые девочки знакомы между собой. А у каждой девочки среди ее знакомых мальчиков больше, чем девочек. Докажите, что в деревне Гадюкино мальчиков не меньше, чем девочек.
-
Докажите неравенство 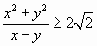 , если известно, что x > y и xy = 1.
, если известно, что x > y и xy = 1.
-
Замок состоит из 64 одинаковых квадратных комнат, имеющих по двери в каждой стене и расположенных
в виде квадрата 8´8. Полы в комнатах покрашены в белый цвет. Каждое утро маляр совершает прогулку по замку, причем, проходя через комнату он перекрашивает в ней пол в противоположный цвет. Возможно ли, что когда-нибудь в замке полы окажутся покрашенными в шахматном порядке в черные и белые цвета?
-
На сторонах BC и CD квадрата ABCD выбрали точки K и L соответственно.
P1 и P2 – основания перпендикуляров, опущенных на прямые AK и AL из точки
B, Q1 и Q2 – основания перпендикуляров, опущенных на прямые AK и AL из точки D. Докажите, что отрезки P1P2 и Q1Q2 равны и перпендикулярны.
-
На совместной конференции партий лжецов и правдолюбов в президиум было избрано 32 человека,
которых рассадили в четыре ряда по 8 человек. В перерыве каждый член президиума заявил, что среди его соседей есть
представители обеих партий. Известно, что лжецы всегда лгут, а правдолюбы всегда говорят правду. При каком наименьшем числе лжецов в президиуме возможна описанная ситуация? (Два члена президиума являются соседями, если один из них сидит слева, справа, спереди или сзади от другого).
В треугольнике ABC I – центр вписанной окружности. Пусть N,
M середины сторон AB и CA соответственно. Прямые BI и CI пересекают
MN в точках K и L соответственно. Докажите, что AI + BI + CI > BC + KL.
Пусть p и q взаимно-простые натуральные числа такие, что:
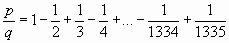 Докажите, что p делится на 2003.
Докажите, что p делится на 2003.
В клетках таблицы m´
n расставлены числа +1 и –1. Известно, что в начале ровно в одной клетке стоит –1,
а в остальных +1. На каждом ходу разрешается заменить –1 на 0, а все соседние по стороне клетки умножить на –1.
Найдите все пары m и n при которых, при любом расположении (–1),
заданными операциями можно получить таблицу из 0.
n1, n2, ... , n1998 натуральные числа,
такие что 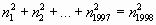 Докажите, что не менее двух из них четны.
Докажите, что не менее двух из них четны.
Равнобедренные, подобные треугольники QPA и SPB построены во вне параллелограмма
PQRS (где PQ = AQ и PS = BS). Докажите что RAB, QPA и SPB подобны.
Профессор сказал Пете сумму двух натуральных чисел, а Серёже их произведение.
В начале, никто из них не знал число другого.
Один из них говорит: Ты не сможешь угадать моё число.
Второй отвечает: Ты не прав, это число 136.
Какие числа им сказал профессор? Ответ обоснуйте.
На международной встрече участвовало n ³
3 человек, говоривших на 14 языках. Известно, что:
– Любые 3 участника знают могут общаться на одном языке.
– Ни один язык не знает более половины участников.
Найдите наименьшее значение n.
Пусть p, q, r действительные положительные числа, а n натуральное.
Докажите, что если pqr = 1 то тогда 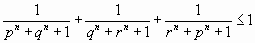 .
.
На доске написано уравнение х3 + ...х2 + ...х + ...= 0. Двое играют в такую игру: первый ставит на любое из пустых мест целое число, отличное от нуля. Затем второй ставит целое число, отличное от нуля, на одно из оставшихся мест. Наконец, первый ставит целое число, отличное от нуля, на последнее место. Докажите, что первый может играть так, что независимо от хода второго все три корня получившегося уравнения оказались целыми числами.
Можно ли покрыть всю плоскость квадратами, среди которых не будет равных между собой.
На выпускном вечере старшеклассников собралось несколько юношей и девушек. При этом оказалось,
что если выбрать любую группу юношей, то число девушек, знакомых по крайней мере с одним из юношей этой группы,
будет не меньше числа юношей в группе. Доказать, что все юноши одновременно смогут танцевать каждый в паре со знакомой девушкой.
Определите вид четырехугольника АВСD площади S, если внутри его существует точка О,
для которой выполняется равенство 2S = ОА2 + ОВ2 +
ОС2 + OD2.
Высоты треугольника АВС пересекаются в точке О, а точки
А1, В1, С1 являются серединами сторон ВС, СА, АВ соответственно.
Окружность с центром в О пересекает прямую В1С1 в точках Д1,
Д2,
прямую С1А1 – в точках Е1, Е2, а прямую
А1В1 –
в точках F1, F2. Докажите, что АД1 = АД2 = ВЕ1 =
ВЕ2 = СF1 = СF2.
На столе лежит куб с ребром 5 состоящий из кубиков с ребром 1. Мальчик разбирает его по следующему правилу: после того, как он взял очередной кубик, следующий он берёт только тот, который имел общую грань с только что взятым кубиком. Может ли так оказаться, что после очередного хода останется столбик из кубиков с ребром 1 и высоты 5, содержащий при этом центральный кубик. Если да, то постройте алгоритм действий мальчика.
При каких натуральных значениях k существуют положительные числа 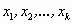 , удовлетворяющие системе уравнений
, удовлетворяющие системе уравнений 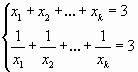 . Найдите эти числа.
. Найдите эти числа.
Существуют ли натуральные числа, которые ровно семью способами можно представить в виде разности квадратов натуральных чисел.
В треугольнике ABC I – центр вписанной окружности. Пусть N,
M середины сторон AB и CA соответственно. Прямые BI и CI пересекают
MN в точках K и L соответственно. Докажите, что AI + BI + CI > BC + KL.
Найти все целые a, b, c, d, a>b>c>d такие, что ab+cd=34 и ac–bd=19.
В клетках таблицы m´
n расставлены числа +1 и –1. Известно, что в начале ровно в одной клетке стоит –1,
а в остальных +1. На каждом ходу разрешается заменить –1 на 0, а все соседние по стороне клетки умножить на –1.
Найдите все пары m и n при которых, при любом расположении (–1),
заданными операциями можно получить таблицу из 0.
На международной встрече участвовало n ³
3 человек, говоривших на 14 языках. Известно, что:
– Любые 3 участника знают могут общаться на одном языке.
– Ни один язык не знает более половины участников.
Найдите наименьшее значение n.
Пусть p, q, r действительные положительные числа, а n натуральное.
Докажите, что если pqr = 1 то тогда 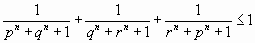 .
.
Найдите все многочлены двух переменных P(x,y) такие, что P(a,b)P(c,d) = P(ac+bd,ad+bc), "
a, b, c, d Î R.
В тетраэдре ABCD угол BAC равен углу ACD, а угол ABD равен углу BDC. Докажите, что AB = CD.
Являясь боссом компании, вы должны распределить 10 человек по 10 заданиям.
У каждого человека для каждого задания есть два числовых параметра – способность и энтузиазм.
Сотрудник будет недоволен распределением, если есть задача, к которой у него больший энтузиазм,
а ей занимается сотрудник с меньшей способностью. Распределение называется плохим, если задачи
можно перераспределить так, чтобы каждую решал сотрудник с большей способностью.
Докажите, что существует неплохое распределение без недовольных.
- Дан трехгранный угол с вершиной О, все плоские углы которого прямые.
На его ребрах выбираются точки А, В и С по одной на каждом.
Найдите геометрическое место точек пересечения биссектрис всевозможных треугольников АВС.
Из точки Р внутри остроугольного треугольника АВС
опущены перпендикуляры РА1, РВ1 и РС1
на стороны ВС, СА и АВ соответственно.
Определите положение точки Р, если известно, что все три четырехугольника
РА1ВС1, РВ1СА1
и РС1АВ1 – описанные.
Могло ли так случиться, что в некоторой компании людей
любые двое знакомых имеют ровно одного общего знакомого, а любые двое незнакомых имеют не менее 5 общих знакомых?
Определите вид четырехугольника АВСD площади S,
если внутри его существует точка О, для которой выполняется равенство 2S = ОА2 +
ОВ2 + ОС2 + OD2.
По окружности расставлены 100 чисел, каждое из которых равно либо 2,
либо 5, либо 9, причем никакие два равных числа не стоят рядом. Числа разбили на 50 пар рядом стоящих.
Числа в парах перемножили и полученные 50 произведений записали на первую доску. Затем эти же
100 чисел разбили на 50 пар рядом стоящих другим способом, числа в парах снова перемножили и записали на вторую доску.
Докажите, что суммы чисел, написанных на первой и второй досках, равны.
Пусть 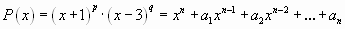 , где p и q– натуральные числа.
Докажите, что если
, где p и q– натуральные числа.
Докажите, что если 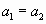 , то 3n – точный квадрат.
, то 3n – точный квадрат.
При каких натуральных значениях k существуют положительные числа
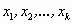 , удовлетворяющие системе уравнений
, удовлетворяющие системе уравнений
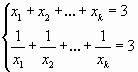 . Найдите эти числа.
. Найдите эти числа.
Существуют ли натуральные числа, которые ровно семью способами можно представить в виде разности квадратов натуральных чисел?
![]()
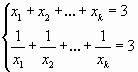 . Найдите эти числа.
. Найдите эти числа.