- Делители
. Известно, что числа x и y взаимно просты. Докажите, что числа (x+y) и (x2-xy+y2) не могут иметь общего делителя, большего 3.
- Заборы
. На плоскости отметили n точек и n-2 непересекающихся отрезка. Докажите, что найдутся две точки, которые "видят" друг друга (точки не лежат на отрезках).
- Ромб
. В ромбе ABCD угол А равен 60º. На стороне AD отмечена точка
N, на стороне CD – точка M, причем один из углов треугольника BMN равен 60º. Докажите, что все углы треугольника BMN равны 60º.
- Эскалатор
. Найдите глубину залегания метро по следующим данным.
Если мы стоим на эскалаторе, то спуск занимает 3 мин., а если мы идём по эскалатору, то спуск занимает 1 мин.
и мы проходим 120 ступенек. Высота ступеньки 20 см. (Эскалатор считаем прямым).
- Перпендикуляры
Из точки внутри выпуклого
многоугольника опускают перпендикуляры на его стороны или их продолжения. Докажите, что хотя бы один
перпендикуляр попадёт на сторону (а не ее продолжение).
- Отрезки
. 50 красных и 50 синих точек делят окружность
на 100 равных дуг. Все красные точки соединили между собой отрезками и все синие – между собой. Докажите, что набор красных отрезков совпадает с набором синих отрезков. (Все красные и синие отрезки можно разбить на пары равных отрезков разного цвета.)
- Алгоритм
. На плоскости нарисованы несколько окружностей, причем, двигаясь по дугам можно пройти до любой точки. Докажите, что эту систему окружностей можно нарисовать, не отрывая карандаша от бумаги и не проводя никакую дугу дважды (точки пересечения дуг дугами не считаются).
- Прямоугольники
. Квадрат разделен на 5 прямоугольников так, что четыре
из них имеют общий угол с квадратом, а пятый – в середине (не граничит с квадратом). Известно, что площади четырех "угловых" прямоугольников равны. Докажите, что в середине – квадрат.
В командной олимпиаде участвовали три команды. Но каждая команда имела два названия.
Сдавая задачу, называлось либо одно, либо другое название.
Увидев итоговую таблицу (см. справа), председатель жюри заставил жюри восстановить результаты,
определив как названия объединяются в пары. Как выполнить эту задачу, используя только таблицу?
Автомобиль проехал расстояние от Костромы до Москвы со
средней скоростью 50 км/ч. При этом сначала он двигался со скоростью 40 км/ч, а с какого-то момента – со
скоростью 60 км/ч. Какую часть пути автомобиль ехал со скоростью 40 км/ч?
Сумма кубов трех чисел более утроенного произведения на 15. Сумма чисел равна 3.
Чему равна сумма квадратов этих чисел?
Точка О – центр параллелограмма АВСD.
Можно ли однозначно восстановить этот параллелограмм, если известно положение середин отрезков АВ,
АD и ОС?
В ряд стоят N человек. Если бы из ряда вышел каждый третий, а потом из оставшихся –
каждый четвертый, то ряд уменьшился бы на 27 человек. Но если бы из ряда вышел сначала каждый четвертый,
а потом каждый третий, то ряд
уменьшился бы на также на 26 человек. Чему могло равняться N?
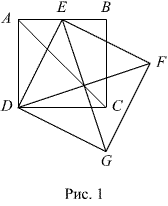
Квадраты ABCD и DEFG расположены так, что точка
E лежит на стороне AB, а сторона EF пересекает сторону BC (рисунок 1).
Докажите, что центр квадрата DEFG лежит на диагонали AC квадрата ABCD.
Существуют ли такие 19 различных натуральных чисел, что произведение любых
10 чисел кратно произведению оставшихся 9 чисел?
В некотором государстве 25 городов, которые объединены сетью
из 24 дорог. Каждая дорога соединяет два города и ее длина равна 100 км. Составили справочник,
который для каждой пары городов указывает расстояние, которое надо проехать от одного города до другого
по дорогам. Сумма всех указанных чисел равна 122500 км. Математик Вася, узнав только это, утверждает:
"В справочнике есть ошибка". Кто ошибается: Вася или справочник?
Числовая функция для любых действительных чисел x, y удовлетворяет равенству f(x+y)=f(x)+f(y)+80xy. Найти f(4/5), если f(1/4)=2.
Пользуясь шаблоном, имеющим форму полукруга, проведите через данную точку на прямой перпендикуляр к этой прямой (шаблон можно обводить по его границе).
Решите уравнение
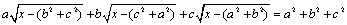 где a, b, c – заданные положительные числа.
где a, b, c – заданные положительные числа.
На доске написаны 10 произвольных натуральных чисел. Докажите, что ставя перед каждым числом плюс или минус, можно добиться того, чтобы алгебраическая сумма нескольких из этих чисел делилась на 1001.
На плоскости дано n точек. Доказать, что их можно соединить несамопересекающейся ломаной с вершинами в этих точках.
На одной стороне угла с вершиной O расположены последовательно точки A, B, C так, что OA:AB:BC=1:2:3. На другой стороне угла последовательно расположены точки A1, B1,C1 так, что OA1: A1B1: B1C1=3:3:2. Доказать, что прямые AA1, BB1, CC1 пересекаются в одной точке.
В правильном шестиугольнике некоторые пары вершин соединены отрезками, и каждый отрезок покрашен в синий или красный цвет. Докажите, что если проведено 15 отрезков, то найдутся по крайней мере два треугольника, стороны каждого из которых окрашены в один цвет (не обязательно один и тот же для обоих треугольников).
На круглом столе радиуса R расположено n круглых монет радиуса r, r<R, так, что больше нельзя положить ни одной монеты. Докажите, что 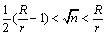 .
.
Вычислите tg 1º – tg 3º + tg 5º – ... – tg 87º + tg 89º.
Двое играют на листе бумаги. Первый на своем ходе рисует
кружок и, если хочет, соединяет его с некоторыми уже нарисованными
кружками, но так, чтобы линии не пересекались (кружки, соединенные линиями,
будем называть соседними); второй же ставит в этот кружок любое
натуральное число, которое отличается от всех чисел в соседних
кружках. Первый хочет заставить второго поставить число, большее
девяти, а второй хочет обойтись только цифрами. Кто победит при
правильной игре?
Для какого многоугольника, лежащего в данном круге, отношение площади к
числу сторон будет наибольшим?
На некотором множестве действует операция x, удовлетворяющая
условиям:
– для любых A, B, C верно, что Ax(BxC)=Bx(CxA);
– если AxB=AxC, то B=C.
Докажите, что операция x коммутативна и ассоциативна.
Окружность радиуса 2006 не проходит через точки единичной
решетки. Точка решетки называется граничной, если она и хотя бы одна из
соседних с ней лежат по разные стороны окружности. Найдите разность между
числом внешних и внутренних граничных точек.
Пусть M – середина стороны AD параллелограмма ABCD, N –
проекция M на прямую BC, X – произвольная точка на продолжении отрезка
CD за точку D, Y – точка пересечения прямых MX и AC. Докажите, что
NM – биссектриса угла XNY.
Существует ли набор из 2006 различных натуральных чисел, в котором любые
два числа взаимно просты, а сумма любых двух или более чисел – составное
число?
Чемпион мира по волейболу определяется в однокруговом турнире n
команд. Среди этих команд k, представляющих Европу, в играх между собой
определяют чемпиона Европы. При каком наибольшем k команда, занявшая чистое
первое место в чемпионате Европы, может занять чистое последнее место в
чемпионате мира?
Четырехугольник ABCD вписан в окружность. T – точка пересечения его диагоналей.
M, N, P, Q – основания перпендикуляров, опущенных из точки T на стороны AB, BC, CD, DA.
Всегда ли в четырехугольник MNPQ можно вписать окружность?
Найдите все трехзначные числа N такие, что любая натуральная степень N оканчивается на N.
На математическую олимпиаду пришло 100 человек. Может ли так быть, что каждый не знаком по крайней мере с 66 из остальных, но среди любых 4 присутствующих найдутся двое, знакомые друг с другом?
На плоскости дана прямая l и точки A и B в одной полуплоскости относительно l.
Найдите на l такую точку C, что в треугольнике ABC отрезок, соединяющий основания высот из вершин A и B, имеет наименьшую возможную длину.
Коля записал в ряд n чисел, каждое из которых 1 или –1 (n>4). Петя знает количество чисел n.
Он может узнать у Коли произведение любых трёх чисел. За какое наименьшее количество вопросов он может узнать произведение всех чисел, написанных Колей?
Пусть x, y, z – положительные числа и x+y+z=1.Докажите, что выполняется неравенство 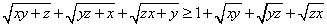
Все вершины правильного семнадцатиугольника раскрашены в 3 цвета так, что
любые две соседние вершины разного цвета. Всегда ли его можно разрезать
непересекающимися диагоналями на треугольники, у каждого из которых все
вершины разного цвета?
S – множество целых чисел такое, что все целые корни любого многочлена с коэффициентами из S
также принадлежат S. Какое наименьшее количество элементов может быть в S, если известно, что 0 принадлежит S и 8 принадлежит S?
Дан тетраэдр. 4 шара с центрами в его вершинах покрывают его
весь. Вершины тетраэдра сдвинули так, что ни одно его ребро не увеличилось
(радиусы шаров не изменились). Верно ли, что шары по-прежнему покрывают
тетраэдр?
Двое играют на листе бумаги. Первый на своем ходе рисует
кружок и, если хочет, соединяет его с некоторыми уже нарисованными
кружками, но так, чтобы линии не пересекались (кружки, соединенные линиями,
будем называть соседними); второй же ставит в этот кружок любое
натуральное число, которое отличается от всех чисел в соседних
кружках. Первый хочет заставить второго поставить число, большее
девяти, а второй хочет обойтись только цифрами. Кто победит при
правильной игре?
На некотором множестве действует операция x, удовлетворяющая
условиям:
– для любых A, B, C верно, что Ax(BxC)=Bx(CxA);
– если AxB=AxC, то B=C.
Докажите, что операция x коммутативна и ассоциативна.
Окружность радиуса 2006 не проходит через точки единичной
решетки. Точка решетки называется граничной, если она и хотя бы одна из
соседних с ней лежат по разные стороны окружности. Найдите разность между
числом внешних и внутренних граничных точек.
Пусть M – середина стороны AD параллелограмма ABCD, N –
проекция M на прямую BC, X – произвольная точка на продолжении отрезка
CD за точку D, Y – точка пересечения прямых MX и AC. Докажите, что
NM – биссектриса угла XNY.
Существует ли набор из 2006 различных натуральных чисел, в котором любые
два числа взаимно просты, а сумма любых двух или более чисел – составное
число?
Уравнение
xn+a1xn-1+...+ak-1xn-k+1+ak+1xn-k-1+...+a
n=0 имеет n действительных корней. Докажите, что ak-1ak+1<0.
Чемпион мира по волейболу определяется в однокруговом турнире n
команд. Среди этих команд k, представляющих Европу, в играх между собой
определяют чемпиона Европы. При каком наибольшем k команда, занявшая чистое
первое место в чемпионате Европы, может занять чистое последнее место в
чемпионате мира?
Во вписанном четырехугольнике ABCD точки M и N – середины сторон
АВ и CD соответственно. Точка Р лежит на отрезке MN, причём МP =
CN и NP = AM. Точка О – центр описанной
окружности четырехугольника. Докажите, что, если точки О и Р не совпадают, то
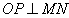 .
.
Докажите, что всех действительных значениях х справедливо неравенство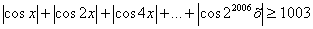 .
.
Докажите, что для любого натурального числа n число nn+1 + (n + 1)n+2 + (n + 2)n+3 является составным.
Площади четырех граней одного тетраэдра равны площадям четырех граней другого тетраэдра. Верно ли, что объемы этих тетраэдров равны?
S
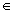 S и 1000
S и 1000 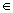 S.
S.
Произведение трех последовательных нечетных чисел в 5 раз меньше числа 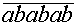 . Найдите эти нечетные числа.
. Найдите эти нечетные числа.
На плоскости находятся 2006 красных точек, причем никакие три из них не лежат на одной прямой. Известно, что площадь треугольника с вершинами в любых трех из этих точек меньше 1. Докажите, что существует треугольник площади меньше 1, который содержит не менее 502 красных точек.
В компании у каждых двух людей ровно пять общих знакомых. Докажите, что количество пар знакомых делится на 3.

