Задача 1 (мозаика, 3 балла)
Нарисована фигура, из которой можно получить правильную, добавив или убрав один ромб
2
Нарисована фигура, из которой можно получить правильную, убрав один ромб и добавив другой
1
Нарисована фигура, содержащая 8 «широких» и 3 «узких» ромба
1
Задача 2 (цветы, 4 балла)
Рассмотрен частный случай; правильный ответ не получен.
0
Верный ответ получен из неверных рассуждений
0
Верный ответ без пояснений или верный ответ, полученный из рассмотрения частного случая
1
Сформулировано, что 10-й тюльпан со стороны Синеглазки и 6-й со стороны Незнайки — это один и тот же цветок, если только это не основано на рассмотрении частного случая, правильный ответ не получен
2
Правильный ход решения с ошибкой на ±1 на каком-то шаге (например, 30-11=20)
3
Задача 3 (север-юг, 4 балла)
Ответ «выиграет Юг» без обоснования
0
Ответ «выиграет Юг со счётом 2:1» без обоснования
1
Верный ответ, но в обосновании забыт случай ничьей
2
Доказано, что Север проиграл, но не найдено, с каким счётом
2
Верный ответ, но не обосновано, почему прогноз д) верен
2
Задача 4 (геометрия, 6 баллов)
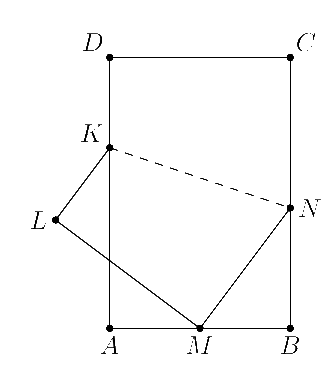
Стандартное решение задачи состоит
из нескольких шагов.
За каждый шаг начислялось своё количество баллов.
Перепутаны прямая и обратная теорема, в остальном решение верное
5
Доказано, что DK=KL
«+1»
Правильно сказано, который катет равен которому
«+2»
Доказано, что LM=CD=AK
«+2»
Правильный ответ. Этот балл начислялся только при условии наличия какого-то из остальных продвижений.
«+1»
Задача 5 (землетрясение, 6 баллов)
Сказано, что в слове ЗЕМЛЕТРЯСЕНИЕ встречаются все 10 цифр
2
Утверждается, но не обосновано, почему число обязательно делится на 3
2
Сказано, что встречаются все 10
цифр, из этого без дополнительных пояснений
делается вывод, что число делится на 3.
4
В целом решение правильное, но не сказано явно, что встречаются все 10 цифр
5
Доказано, что число делится на 3
6
Задача 6 (таблица, 1+2+3 баллов)
Нет примера для п. а), но есть правильный пример для п. б)
1+2+.
Неправильный пример для п. а) и правильный пример для б)
0+2+.
Правильный пример для (а), нет или неправильный пример для (б)
1+0+.
Сформулировано, что наименьшее из
чисел не в углу отмечено не будет
(в дополнительном обосновании не нуждается)
.+.+3
При доказательстве от противного доказано только, что числа 1, 2, 3, 4 должны стоять в углах
.+.+1