13-й Математический Праздник.
17 февраля 2002 года

Условия задач.

6 класс

Задача 1.
Решите ребус: БАО*БА*Б=2002. [3 балла] (А. Блинков, А. Хачатурян)

Задача 2.
Незнайка разрезал фигуру на трёхклеточные и четырёхклеточные уголки, нарисованные справа от неё. Сколько трёхклеточных уголков могло получиться? [4 балла] (А. Митягин)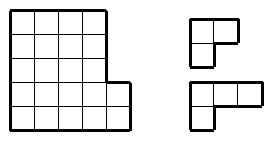

Задача 3.
На доске были написаны 10 последовательных натуральных чисел. Когда стёрли одно из них, то сумма девяти оставшихся оказалась равна 2002. Какие числа остались на доске? [6 баллов] (В. Произволов)

Задача 4.
Художник-авангардист Змий Клеточкин покрасил несколько клеток доски размером 7*7, соблюдая правило: каждая следующая закрашиваемая клетка должна соседствовать по стороне с предыдущей закрашенной клеткой, но не должна - ни с одной другой ранее закрашенной клеткой. Ему удалось покрасить 31 клетку.

Побейте его рекорд - закрасьте
а) 32 клетки - [2 балла];
б) 33 клетки - [3 балла]. (И. Акулич)

Задача 5.
Илье Муромцу, Добрыне Никитичу и Алёше Поповичу за верную службу дали 6 монет: 3 золотых и 3 серебряных. Каждому досталось по две монеты. Илья Муромец не знает, какие монеты достались Добрыне, а какие Алёше, но знает, какие монеты достались ему самому. Придумайте вопрос, на который Илья Муромец ответит "да", "нет" или "не знаю", и по ответу на который Вы сможете понять, какие монеты ему достались. [6 баллов] (А. Чеботарёв)

Задача 6.
Айрат выписал подряд все числа месяца:

123456789101112...