14-й Математический Праздник.
16 февраля 2003 года

Условия задач.

6 класс

Задача 1. [4 балла]
Один мальчик 16 февраля 2003 года сказал: "Разность между числами прожитых мною месяцев и прожитых (полных) лет сегодня впервые стала равна 111". Когда он родился?

Задача 2. [4 балла]
Найдите наименьшее четырехзначное число СЕЕМ, для которого существует решение ребуса
МЫ + РОЖЬ = СЕЕМ.
(Одинаковым буквам соответствуют одинаковые цифры, разным — разные.

Задача 3. [4 балла]
На острове живут рыцари, которые всегда говорят правду, и лжецы, которые всегда лгут. Путник встретил троих островитян и спросил каждого из них: "Сколько рыцарей среди твоих спутников?". Первый ответил: "Ни одного". Второй сказал: "Один". Что сказал третий?

Задача 4. [5 баллов]
Прямоугольник разрезан на несколько прямоугольников, периметр каждого из которых — целое число метров. Верно ли, что периметр исходного прямоугольника — тоже целое число метров?

Задача 5. [7 баллов]
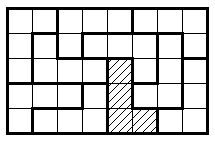
В распоряжении юного паркетчика имеются 10 одинаковых плиток, каждая из которых состоит из 4 квадратов и имеет форму буквы Г (все плитки ориентированы одинаково). Может ли он составить из них прямоугольник размером 5*8? (Плитки можно поворачивать, но нельзя переворачивать. Например, на рисунке изображено неверное решение: заштрихованная плитка неправильно ориентирована.)

Задача 6. [8 баллов]
На гранях кубика расставлены числа от 1 до 6. Кубик бросили два раза. В первый раз сумма чисел на четырех боковых гранях оказалась равна 12, во второй — 15. Какое число написано на грани, противоположной той, где написана цифра 3?

Дата последнего изменения — 17 февраля 2003 года