18-й Математический Праздник.
11 февраля 2007 года

Условия задач.

На выполнение заданий отводилось 2 часа (120 минут), для записи решений школьникам предлагались специальные бланки (Бланк с заданиями 6 класса: blank6.ps - 218 Кб, blank6.pdf - 111 Кб.) Также всем участникам были выданы вырезанные из плотной бумаги фигурки, упомянутые в условии задачи 5.

6 класс

Задача 1. [4 балла] По двум телевизионным каналам одновременно начали показывать один и тот же фильм. На первом канале фильм разбили на части по 20 минут каждая и вставили между ними двухминутные рекламные паузы. А на втором канале фильм разбили на части по 10 минут каждая и вставили между ними минутные рекламные паузы. На каком канале фильм закончится раньше?

Задача 2. [4 балла] В конце четверти Вовочка выписал подряд в строчку свои текущие отметки по пению и поставил между некоторыми из них знак умножения. Произведение получившихся чисел оказалось равным 2007. Какая отметка выходит у Вовочки в четверти по пению? ("Колов" учительница пения не ставит.)

Задача 3. [5 баллов] Волк с тремя поросятами написал детектив "Три поросёнка--2", а потом вместе с Красной Шапочкой и её бабушкой кулинарную книгу "Красная Шапочка-2". В издательстве выдали гонорар за обе книжки поросёнку Наф-Нафу. Он забрал свою долю и передал оставшиеся 2100 золотых монет Волку. Гонорар за каждую книгу делится поровну между её авторами. Сколько денег Волк должен взять себе?

Задача 4. [6 баллов] В Совершенном городе шесть площадей. Каждая площадь соединена прямыми улицами ровно с тремя другими площадями. Никакие две улицы в городе не пересекаются. Из трёх улиц, отходящих от каждой площади, одна проходит внутри угла, образованного двумя другими. Начертите возможный план такого города.

Задача 5. [7 баллов] Нарисуйте, как из данных трёх фигурок, использовав каждую ровно один раз, сложить фигуру, имеющую ось симметрии.

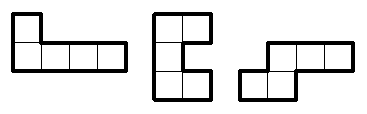
Задача 6. [4(а)+5(б)=9 баллов] Кощей Бессмертный похитил у царя трёх дочерей. Отправился Иван-царевич их выручать. Приходит он к Кощею, а тот ему и говорит:

"Завтра поутру увидишь пять заколдованных девушек. Три из них - царевы дочери, а ещё две - мои. Для тебя они будут неотличимы, а сами друг дружку различать смогут. Я подойду к одной из них и стану у неё спрашивать про каждую из пятерых: "Это царевна?". Она может отвечать и правду, и неправду, но ей дозволено назвать царевнами ровно двоих (себя тоже можно называть). Потом я так же опрошу каждую из остальных девушек, и они тоже должны будут назвать царевнами ровно двоих. Если после этого угадаешь, кто из них и вправду царевны, отпущу тебя восвояси невредимым. А если ещё и догадаешься, которая царевна старшая, которая средняя, а которая младшая, то и их забирай с собой."

Иван может передать царевнам записку, чтобы научить их, кого назвать царевнами. Может ли он независимо от ответов Кощеевых дочерей:
а) вернуться живым [4 балла];
б) увезти царевен с собой? [5 баллов]?

Опубликовано 11 февраля 2007 года