13-й Математический Праздник.
17 февраля 2002 года

Условия задач.

7 класс

Задача 1.
2002 год - год-палиндром, то есть одинаково читается справа налево и слева направо. Предыдущий год-палиндром был 11 лет назад (1991). Какое максимальное число годов-непалиндромов может идти подряд (между 1000 и 9999 годами)? [5 баллов] (Г. Гальперин, Д. Григоренко)

Задача 2.
Незнайка разрезал фигуру на трёхклеточные и четырёхклеточные уголки, нарисованные справа от неё. Сколько трёхклеточных уголков могло получиться? [5 баллов] (А. Митягин)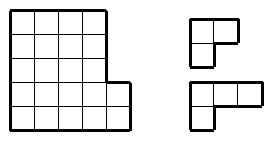

Задача 3.
В написанном на доске примере на умножение хулиган Петя исправил две цифры. Получилось 4*5*4*5*4=2247. Восстановите исходный пример и объясните, как Вы это сделали. [5 баллов] (И. Ященко)

Задача 4.
У Васи есть пластмассовый угольник (без делений) с углами 30^o, 60^o и 90^o. Ему нужно построить угол в 15^o. Как это сделать, не используя других инструментов? [5 баллов] (М. Панов)

Задача 5.
Художник-авангардист Змий Клеточкин покрасил несколько клеток доски размером 8*8, соблюдая правило: каждая следующая закрашиваемая клетка должна соседствовать по стороне с предыдущей закрашенной клеткой, но не должна - ни с одной другой ранее закрашенной клеткой. Ему удалось покрасить 36 клеток. Побейте его рекорд!

(За 39 клеток - [2 балла], за каждую следующую клетку - ещё [по 2 балла]. Жюри умеет закрашивать 42 клетки!) (И. Акулич)

Задача 6.
В шахматном турнире на звание мастера спорта участвовало 12 человек, каждый сыграл с каждым по одной партии. За победу в партии даётся 1 очко, за ничью - 0,5 очка, за поражение - 0 очков. По итогам турнира звание мастера спорта присваивали, если участник набрал более 70% от числа очков, получаемых в случае выигрыша всех партий. Могли ли получить звание мастера спорта
а) 7 участников [4 балла];
б) 8 участников [6 баллов]? (Е. Иванова)

Дата последнего изменения: 21 февраля 2002 года