16-й Математический Праздник.
13 февраля 2005 года

Условия задач.

На выполнение заданий отводилось 2 часа (120 минут), для записи решений школьникам предлагались специальные бланки (скачать бланки 7 класса в формате Zip-PostScript - 77 Кб)

7 класс

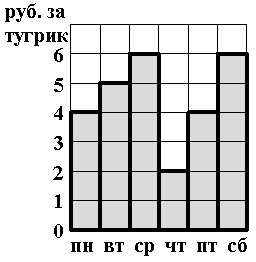
Задача 1. [3 балла] На рисунке изображено, как изменялся курс тугрика в течение недели. У Пети было 30 рублей. В один из дней недели он обменял все свои рубли на тугрики. Потом он обменял все тугрики на рубли. Затем он ещё раз обменял все вырученные рубли на тугрики, и в конце концов, обменял все тугрики обратно на рубли. Напишите, в какие дни он совершал эти операции, если в воскресенье у него оказалось 54 рубля. (Достаточно привести пример.)

Задача 2. Можно ли расставить числа
а) [3 балла] от 1 до 7;
б) [3 балла] от 1 до 9
по кругу так, чтобы любое из них делилось на разность своих соседей?

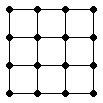
Задача 3. [4 балла] Зачеркните все шестнадцать точек, изображённых на рисунке, шестью отрезками, не отрывая карандаша от бумаги и не проводя отрезков по линиям сетки.

Задача 4. Бумага расчерчена на клеточки со стороной 1. Ваня вырезал из неё по клеточкам прямоугольник и нашёл его площадь и периметр. Таня отобрала у него ножницы и со словами "Смотри, фокус!" вырезала с краю прямоугольника по клеточкам квадратик, квадратик выкинула и объявила: "Теперь у оставшейся фигуры периметр такой же, какая была площадь прямоугольника, а площадь - как был периметр!" Ваня убедился, что Таня права.
а) [2 балла] Квадратик какого размера вырезала и выкинула Таня?
б) [3 балла] Приведите пример такого прямоугольника и такого квадрата.
в) [4 балла] Прямоугольник каких размеров вырезал Ваня?

Задача 5. Решите ребус 250*ЛЕТ+МГУ=2005*ГОД. (Разными буквами обозначены разные цифры, а одинаковыми - одинаковые; при этом некоторыми буквами могут быть обозначены уже имеющиеся цифры 2, 5 и 0.)
а) [4 балла] Найдите хотя бы одно решение ребуса;
б) [4 балла] Докажите, что других решений нет.

Задача 6. [8 баллов] На острове Невезения с населением 96 человек правительство решило провести пять реформ. Каждой реформой недовольна ровно половина всех граждан. Гражданин выходит на митинг, если он недоволен более чем половиной всех реформ. Какое максимальное число людей правительство может ожидать на митинге? (Приведите пример и докажите, что больше нельзя.)

Дата последнего изменения — 13 февраля 2005 года