17-й Математический Праздник.
12 февраля 2006 года

Условия задач.

На выполнение заданий отводилось 2 часа (120 минут), для записи решений школьникам предлагались специальные бланки (скачать бланки 7 класса в формате Zip-PostScript - 163 Кб)

7 класс

Задача 1. [4 балла] Винни-Пух и Пятачок поделили между собой торт. Пята- чок захныкал, что ему досталось мало. Тогда Пух отдал ему треть своей доли. От этого у Пятачка количество торта увеличилось втрое. Какая часть торта была вначале у Пуха и какая у Пятачка?

Задача 2. [5 баллов] Разрежьте нарисованный пятиугольник на две одинаковые (совпадающие при наложении) части.

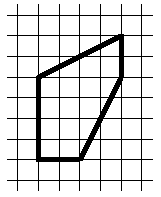
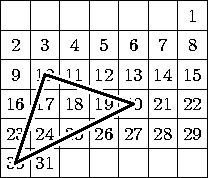
Задача 3. [5 баллов] Наташа сделала из листа клетчатой бумаги календарь на январь 2006 года (см. рисунок) и заметила, что центры клеток 10, 20 и 30 января образуют равнобедренный прямоугольный треугольник. Наташа предположила, что это будет верно и в любом другом году, за исключением тех лет, когда центры клеток 10, 20 и 30 лежат на одной прямой. Права ли Наташа?

Задача 4. Год проведения нынешнего математического праздника делится на его номер:

2006 : 17 = 118.

а) [2 балла] Назовите первый номер матпраздника, для которого это тоже было выполнено.

б) [5 баллов] Назовите последний номер матпраздника, для которого это тоже будет выполнено.

Задача 5. [7 баллов] Дед звал внука к себе в деревню: "Вот посмотришь, какой я необыкновенный сад посадил! У меня там растут груши и яблони, причём яблони посажены так, что на расстоянии 10 метров от каждой яблони растёт ровно две груши". - "Ну и что тут интересного, - ответил внук. - У тебя, значит, яблонь вдвое меньше, чем груш". "Авот и не угадал, - улыбнулся дед. - Яблонь у меня в саду вдвое больше, чем груш". Нарисуйте, как могли расти яблони и груши в саду у деда.

Задача 6. Петя закрасил одну клетку прямоугольника. Саша может закрашивать другие клетки этого прямоугольника по следующему правилу: можно красить любую клетку, у которой нечётное число закрашенных соседей (по стороне). Сможет ли Саша закрасить все клетки прямоугольника (независимо от того, какую клетку выбрал Петя), если размеры прямоугольника
а) [4 балла]   8 * 9 клеток?
б) [7 баллов]   8 * 10 клеток?

Дата последнего изменения — 12 февраля 2006 года