|
||||||||||
30-й Математический Праздник
17 февраля 2019 года
Условия задач
На выполнение заданий отводилось 2 часа (120 минут),
для записи решений школьникам предлагались специальные бланки
(бланк с заданиями 6 класса: blank6.pdf;
7 класса: blank7.pdf).
6 класс
Задача 1. [4 балла] (А. В. Шаповалов)
Саша выписала числа от одного до ста, а Миша часть из них стёр. Среди оставшихся у 20 чисел есть в записи единица, у 19 чисел есть в записи двойка, а у 30
чисел нет ни единицы, ни двойки. Сколько чисел стёр Миша?
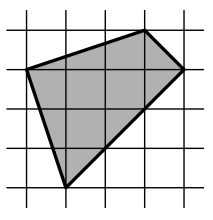
Задача 2. [5 баллов] (М. А. Волчкевич)
Разрежьте фигуру, показанную на рисунке, на четыре одинаковые
части.
Задача 3. [6 баллов] (Е. В. Бакаев)
Сеня не умеет писать некоторые буквы и
всегда в них ошибается. В слове ТЕТРАЭДР он сделал
бы пять ошибок, в слове ДОДЕКАЭДР — шесть, а в слове
ИКОСАЭДР — семь. А сколько ошибок он сделает в слове
ОКТАЭДР?
Задача 4. [не более 6 баллов] (В. А. Клепцын)
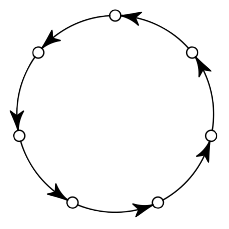
Семь городов соединены по
кругу семью односторонними авиарейсами (см. рисунок). Назначьте (нарисуйте
стрелочками) ещё несколько односторонних рейсов так, чтобы от любого города до
любого другого можно было бы добраться, сделав не более двух пересадок. Постарайтесь сделать число дополнительных рейсов как можно
меньше.
Задача 5. [8 баллов] (Е. В. Бакаев)
Вокруг круглого озера через равные промежутки растут 2019 деревьев: 1009 сосен и 1010 ёлок. Докажите, что обязательно найдется дерево, рядом с которым
растёт сосна и с другой стороны от которого через одно
дерево тоже растёт сосна.
Задача 6. [8 баллов] (А. В. Шаповалов)
Каждая грань куба 6×6×6 разбита на клетки 1×1. Куб оклеили квадратами 2×2 так, что каждый
квадрат накрывает ровно четыре клетки, никакие квадраты не совпадают и каждая клетка накрыта одинаковым
числом квадратов. Какое наибольшее значение может принимать это одинаковое число? (Квадрат можно перегибать
через ребро.)
7 класс
Задача 1. [4 балла] (М. А. Евдокимов, И. В. Раскина)
Ньют хочет перевезти девять фантастических
тварей весом 2, 3, 4, 5, 6, 7, 8, 9 и 10 кг в трёх чемоданах,
по три твари в каждом. Каждый чемодан должен весить
меньше 20 кг. Если вес какой-нибудь твари будет делиться
на вес другой твари из того же чемодана, они подерутся.
Как Ньюту распределить тварей по чемоданам, чтобы никто не подрался?
Задача 2. [5 баллов] (М. А. Хачатурян)
На завтрак группа из 5 слонов и 7 бегемотов
съела 11 круглых и 20 кубических арбузов, а группа из
8 слонов и 4 бегемотов — 20 круглых и 8 кубических арбузов.
Все слоны съели поровну (одно и то же целое число)
арбузов. И все бегемоты съели поровну арбузов. Но один
вид животных ест и круглые, и кубические арбузы, а другой вид привередливый и ест арбузы только одной из форм.
Определите, какой вид (слоны или бегемоты) привередлив
и какие арбузы он предпочитает.
Задача 3. [6 баллов] (Е. В. Бакаев)
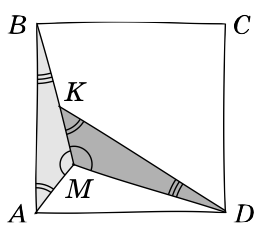
Два равных треугольника
расположены внутри квадрата, как показано на рисунке. Найдите их углы.
Задача 4. [6 баллов] (А. В. Шаповалов)
Имеется три кучки по 40 камней. Петя и Вася
ходят по очереди, начинает Петя. За ход надо объединить
две кучки, после чего разделить эти камни на четыре кучки. Кто не может сделать ход — проиграл.
Кто из играющих (Петя или Вася) может выиграть, как бы ни играл
соперник?
Задача 5. [9 баллов] (М. А. Волчкевич)
Максим сложил на столе из 9 квадратов и 19
равносторонних треугольников (не накладывая их друг на
друга) многоугольник. Мог ли периметр этого многоугольника оказаться равным 15 см, если стороны всех квадратов
и треугольников равны 1 см?
Задача 6. [9 баллов] (С. И. Токарев, А. В. Шаповалов)
В ряд лежат 100 монет, часть — вверх орлом,
а остальные — вверх решкой. За одну операцию разрешается выбрать семь монет, лежащих через равные промежутки
(т.е. семь монет, лежащих подряд, или семь монет,
лежащих через одну, и т.д.), и все семь монет перевернуть.
Докажите, что при помощи таких операций можно все монеты положить вверх орлом.
Опубликовано 22 февраля 2019 года







